Faits divers
Information, Complexité et Musique
Cet article, modifié pour la cause, a fait l'objet d'une radiodiffusion en direct sur la Radio Parfaite, l'antenne officielle du Festival musical du Printemps des Arts de Monte-Carlo, le 19 mars 2017. L'écho différé est disponible ici : .
La complexité des systèmes est un sujet d'étude de la Théorie de l'information telle qu'initiée, au plan syntaxique, par Claude Shannon (1916-2001) et précisée, au plan sémantique, par Andrei Kolmogorov (1903-1987). Elle est présentée informellement ci-dessous et appliquée à l'oeuvre d'art, en particulier musicale.
Chacun pratique à son niveau l'informatique appliquée, l'occasion d'effectuer rapidement des tâches qui s'avéreraient fastidieuses voire impossibles sans elle. Une informatique théorique existe cependant, qui étudie toutes sortes de questions qui nous concernent quoique souvent à notre insu :
- Peut-on tout calculer, en particulier compresser sans perte un message, dans quels délais (Performance temporelle) et en consommant quelle mémoire (Contrainte spatiale) ?
- Peut-on protéger un message contre le bruit, en le dilatant, et dans quelles limites ?
- Peut-on le crypter afin qu'il soit indéchiffrable par un intrus mais parfaitement décodable, à l'identique, par son destinataire mandaté ?
Certes, toutes ces questions sont affaires de spécialistes mais les réponses sont accessibles à un vaste public, notamment celles qui concernent la complexité des systèmes, terme très général qui couvre tous les domaines, scientifique, artistique, etc.
En Sciences
Les systèmes que les scientifiques étudient sont de natures très diverses, en voici trois empruntés aux domaines de la mathématique, de la physique et de la biologie :
-
Pour un mathématicien, un système formel génère des théorèmes à partir d'axiome(s) et de règle(s) logique(s). L'arithmétique de Peano, la géométrie d'Euclide et la théorie des ensembles ne font rien d'autre. L'exemple ci-contre, volontairement schématique, ne contient qu'un seul axiome, codé par la succession de 3 cases noires, et quatre règles logiques dont l'application répétée, ici sur quatre niveaux de profondeur seulement, génère (les démonstrations de) 20 théorèmes. Le lecteur peut imaginer qu'une case noire code "1" et qu'une case blanche code "0", d'où chaque théorème reçoit un énoncé binaire dont la négation s'obtiendrait, par exemple, en inversant les couleurs (Un système formel cohérent ne peut évidemment pas démontrer à la fois un théorème et sa négation, à vérifier dans cet exemple !). En poursuivant éternellement, on dériverait un nombre croissant de théorèmes plus ou moins intéressants qu'on pourrait consigner dans un épais traité. Le point fondamental est que l'énoncé des axiomes et des règles logiques tient dans un petit fichier de quelques centaines de bits à peine, qui suffit à compresser (par programme) la théorie complète. Si un individu, A, veut envoyer, à un correspondant, B, le contenu du traité constitué après N étapes logiques, il n'est pas nécessaire qu'il le transmette in extenso, ce serait inutilement coûteux, il suffit qu'il expédie le programme compresseur. Une machine correctement programmée par B sera alors en mesure de redémontrer et d'imprimer tous les théorèmes, sans même qu'il ait à intervenir.
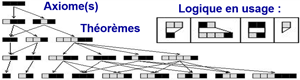
Système formel -
Pour les anciens astronomes, la description du système solaire passait par le relevé quotidien des positions des astres dans le ciel. Après quelques décennies, cela donnait d'énormes registres difficilement gérables. On sait, depuis les travaux de Newton, que toutes ces données obéissent à une logique interne, condensée dans les équations célèbres qui portent son nom. Plus personne aujourd'hui ne passerait son temps à communiquer de tels relevés astronomiques in extenso puisque la donnée des positions des astres à un instant donné, accompagnée des équations d'évolution, suffisent pour prédire l'état du système à n'importe quel moment ultérieur (Sous réserve que le système solaire soit dynamiquement stable sur les trajectoires actuelles, ce que l'on vous souhaite !). En peu de mots, les équations de Newton compressent (par programme) les données relatives au système solaire tout entier et cela pour plusieurs siècles au moins.

Système solaire -
Pour un biologiste, l'organisation des êtres vivants respecte un code génétique qui s'exprime au travers de la structure de son ADN. Celui-ci se présente sous la forme d'une longue double chaîne de bases azotées (Adénine, Cytosine, Guanine et Thymine) ordonnées comme dans ce début de séquence : {T, T, C, A, G, T, T, G, T, G, A, A, T, G, A, A, T, G, G, A, C, G, T, G, C, C, A, A, A, T, A, G, A, C, G, T, G, C, C, G, C, C, G, C, C, G, C, T, C, G, A, T, T, C, G, C, A, C, T, T, T, G, C, T, T, T, C, G, G, T, T, T, T, G, C, C, G, T, C, G, T, T, T, C, A, C, G, C, G, T, T, ...}. Le génome humain comporte quelques milliards de bases qui se suivent dans de longues suites de ce genre. On présume qu'elles sont redondantes afin d'autoriser la correction d'erreurs éventuelles, résultant de mutations intempestives. Compresser sans perte ce génome, c'est sans doute faire en sorte qu'il prenne moins de place en mémoire (et moins de temps à télécharger aux fins de recherches) mais c'est aussi (et à terme surtout) se ménager la possibilité de trouver la logique interne qui organise la succession des bases (Les lois de Newton de la biologie !). Dans le cas de cette science encore jeune, les meilleurs programmes compresseurs ne sont pas encore connus.
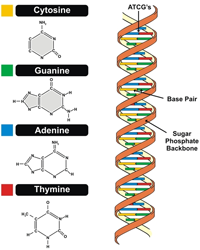
Chaîne ADN, d'après R. Rettner
Dans tous les cas, le programme (de longueur) minimum, capable (de calculer puis) d'imprimer la description du système étudié (à une précision donnée d'avance, c'est un détail technique qu'il est inutile d'expliciter ici), joue un rôle capital. Sa longueur (en bits) définit précisément la complexité algorithmique du système (on dit aussi l'entropie). Qu'un tel programme minimal existe est une évidence puisque sa longueur est un entier positif; qu'il soit calculable est une toute autre affaire. Il n'existe, en effet, pas de procédure algorithmique effective capable de recevoir la description d'un système en entrée et d'en afficher le programme minimum en sortie. Ce n'est nullement le résultat d'une incompétence temporaire de notre part (qu'on pourrait espérer vaincre un jour) mais le résultat d'une indécidabilité fondamentale, inhérente à la théorie de l'information. Si la complexité des systèmes n'est pas calculable en toute généralité, elle s'avère heureusement raisonnablement approximable (par excès) dans un grand nombre de cas.
En littérature
L'exemple littéraire est préparatoire pour la suite. On considère un texte long, rédigé dans une langue connue, par exemple le français. Ce texte se présente comme une suite de lettres, minuscules ou majuscules, éventuellement de chiffres et de divers signes de ponctuation. Les traitements de texte habituels limitent (généreusement !) le nombre des caractères utilisés à 28=256 en sorte que n'importe quel caractère est codable sur 8 bits (de 00000000 à 11111111). Dans ce format (Code ASCII étendu), un texte de 100 000 caractères, encodés littéralement, exige 800 000 bits (soit, en octets, 100 Ko). Peut-on le compresser sans perte afin qu'il occupe moins de place en mémoire ? On devine que la réponse est affirmative, dans certains cas au moins, puisque les fichiers compressés existent, par exemple au format ".zip". Cependant un simple argument de comptage révèle que cette compression ne peut concerner tous les textes, certains seront inévitablement dilatés ! Autrement dit, le compresseur universel ne peut exister.
Note. Si l'argument ne vous paraît pas évident, pensez à un immeuble à étages, en construction, dont tous les appartements ont été achetés sur plans. Si un acheteur se ravise en demandant de descendre d'étage, cela ne pourra se faire qu'à la condition qu'un autre acheteur accepte de monter.
On peut, dès lors, se demander quel est l'intérêt de compresser certains textes si c'est au prix d'en dilater d'autres. La réponse est simple : tous les textes ne se valent pas ! Sur base d'un alphabet comportant 256 caractères, on peut rédiger 256N textes différents, tous de longueur N. C'est un nombre de plus en plus colossal à mesure que N grandit. L'immense majorité de ces textes sont anarchiques d'où aucun algorithme n'a de prise sur eux pour les compresser. Seul un très petit nombre de textes sont porteurs de sens et ce sont eux que les algorithmes compressent en tirant parti des redondances syntaxiques et sémantiques qui les structurent. En résumé, les algorithmes compresseurs contractent efficacement les rares textes structurés, ceux qui nous intéressent, et tant pis s'ils dilatent légèrement les textes aléatoires, infiniment plus nombreux, qui, de toutes façons, ne nous intéressent pas.
On peut tracer un axe des complexités (K) croissantes et y situer les textes (de longueur N) correspondant aux situations extrêmes :
- Du côté des basses complexités, les textes répétitifs du style "aaaa...N fois " sont fortement compressibles par un programme du genre, "Répéter N fois : Print ("a")". La longueur de ce programme (égale à K), est de l'ordre de lg(N) bits car seul l'encodage (binaire) de N est (très modérément) coûteux, dans ce programme, lorsque N grandit.
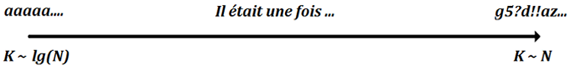
Axe des complexités - Du côté des hautes complexités, les textes aléatoires du style "g5?d!!az..." sont incompressibles car aucun programme imprimant ce texte n'est plus court que "Print(g5?d!!az...)". La complexité, K, est cette fois de l'ordre de N octets puisque le programme consomme un octet par caractère, une simple imprimante ne ferait pas décidément plus mal.
Les textes porteurs de sens se situent évidemment entre ces extrêmes. Leur complexité ne se laisse pas calculer exactement car cela exigerait d'en connaître le programme minimal, chose que nous savons impossible, la plupart du temps. En pratique, on est donc forcé de revoir ses ambitions à la baisse, en se contentant des meilleurs programmes compresseurs trouvables, ce qui demande persévérance, astuce, culture et intelligence. Une stratégie possible met en oeuvre le test de Shannon dont le principe est le suivant.
Un volontaire (ou une machine !) est prié de deviner un texte a priori inconnu, caractère après caractère, en ne posant que des questions binaires (n'appelant que les réponses oui ou non), une sorte de Jeu du Pendu. Lorsque le texte est entièrement trouvé, le nombre, x, de questions posées fournit une (sur)estimation de la complexité du texte (en bits). La surestimation est inévitable car le volontaire ignore la stratégie optimale qui minimiserait le nombre des questions à poser. Pour progresser dans son jeu de devinette, le volontaire dispose de deux armes très différentes, l'une syntaxique et l'autre sémantique :
- Dans toutes les langues praticables, les textes sensés sont syntaxiquement redondants. On signifie par là que les caractères n'y apparaissent pas avec des fréquences égales : tout amateur de Scrabble sait qu'en français, "e" est de loin plus probable que "w". De même, les doublets "es", "de" et "le" sont de loin les plus fréquents, tandis que "qj" ou "wz" n'apparaissent jamais et on pourrait poursuivre avec les triplets, etc. L'ordinateur est imbattable lorsqu'il s'agit de tirer parti de ces redondances de nature statistique : il suffit qu'il mémorise, une fois pour toutes, les tables de fréquences et qu'il cible ses questions en tenant compte de ces données. Le résultat est qu'à a longue, et en moyenne, le nombre de questions binaires peut descendre en-dessous de 2 questions par caractère deviné. Evidemment si le texte avait été aléatoire, rien de tout cela n'aurait fonctionné : le volontaire (ou la machine) n'aurait eu d'autre ressource que de deviner chaque lettre individuellement, en posant autant de questions qu'il y a de chiffres binaires dans le code ASCII de chacune, soit 8 questions par caractère. On constate que les redondances syntaxiques permettent une compression appréciable, d'un facteur 4 environ.
- L'humain prend une revanche éclatante sur la machine lorsqu'il s'agit de poursuivre la compression à l'étape sémantique. Le volontaire peut affiner ses questions en mettant à profit sa connaissance de la langue, le vocabulaire (beaucoup de mots n'existent pas), l'orthographe, la grammaire (respect des accords), la syntaxe (certaines constructions sont bannies) et, par-dessus tout, le sens du discours. A ce jeu de devinette littéraire, l'humain cultivé et intelligent peut anticiper le cours des phrases et battre l'ordinateur, aussi bien préparé que soit celui-ci. En mettant ainsi en pratique de réelles connaissances de la langue, il peut descendre, sur le long terme, à 1.3 questions par caractère.
On peut programmer la compression du texte initial sur la base des redondances syntaxiques, tous les logiciels de compression sans perte le font. On peut même tenter de poursuivre à l'étape sémantique mais il faut garder à l'esprit que l'ordinateur ne pourra aller très loin dans cette direction, en tous cas il n'atteindra jamais l'optimum. Cela n'est pas grave pour la discussion qui nous intéresse car, après tout, personne ne lira jamais un texte dans sa forme compressée. Par contre, tout le monde se sert (in)consciemment des redondances existantes pour le lire avec fluidité. C'est évidemment le cerveau qui anticipe mentalement le déroulement du texte, sur base de ses attentes culturelles, comme s'il s'exerçait, en permanence, au test de Shannon. La phrase précédente, réécrite en forme "texto", si prisée par la nouvelle génération, demeurerait sans doute compréhensible mais elle serait illisible avec l'intonation espérée. Les choses ne se passent pas différemment dans le cas de l'interprétation et de l'écoute musicales : imaginez le désarroi d'un interprète forcé de restituer une sonate de Schubert notée façon "texto", ce serait faisable mais il trébucherait à chaque pas !
On peut présenter les choses autrement et s'intéresser au flux d'information que le cerveau peut traiter intelligemment. On estime qu'un lecteur moyen lit facilement 30 caractères d'un texte français à la seconde, ce qui correspond, en gros, à un débit informationnel de 40 bits/s. Le cerveau en accepte beaucoup plus, en écoute brute, mais s'il doit faire tous les liens nécessaires à la compréhension, 40 bits/s semble une norme acceptable. Les choses ne se passent pas autrement en musique même si l'ordre de grandeur peut varier à la hausse. La plupart des auditeurs (pour ne pas dire tous) ne font pas tous les liens possibles sans que cela affecte leur écoute instantanée. Ils peuvent même s'endormir pendant un quart d'heure sans perdre le fil de l'écoute ultérieure, chose difficilement imaginable en conférence orale. Ce qui est sûr, on reviendra sur ce point, c'est que les musiques d'avant-garde découragent la plupart des auditeurs par leur débit excessif.
En peinture
Un deuxième exemple préparatoire est emprunté au monde de la peinture. On considère quelques systèmes picturaux, du plus simple, une toile uniformément blanche, au plus complexe, une assemblée de points colorés, distribués au hasard. Que la toile blanche (elle pourrait être verte !) soit de complexité (presque) nulle ne surprend personne. Outre que cela semble raisonnable, son programme minimal le confirme, qui se réduit à fixer le nombre des pixels, en abscisse et en ordonnée, plus la couleur uniforme de ceux-ci, au bilan trois nombres entiers suffisent.
-
Considérons, à présent, une représentation (d'un fragment) de l'ensemble fractal de Mandelbrot, un "tube" de la culture mathématique. Aussi étrange que cela puisse paraître, malgré la présence de millions de pixels multicolores, détaillant une structure extrêmement fine (Zoomez ici), la complexité de cet objet est intrinsèquement faible, à peine plus grande que celle du tableau uniformément blanc ! Cela tient au fait qu'il est imprimable au terme de l'exécution d'un programme très court, de quelques lignes à peine. Au plan artistique, cette image ne résiste pas à un regard répété : on peut certes en faire un joli poster pour décorer son bureau mais cela ne lui accordera pas pour autant le statut d'oeuvre d'art.

Ensemble de Mandelbrot -
L'image suivante a été obtenue en répartissant au hasard, dans un cadre carré, 5000 points de couleurs différentes. Elle de complexité maximale (à l'échelle imprimée) car elle est aléatoire par construction. Elle est donc incompressible et aucun programme ne peut être plus concis que celui qui détaille, une à une, les coordonnées de chaque point, ainsi que leur code de couleur. Cette image est peut-être décorative mais elle est interchangeable avec n'importe quel clone facile à imprimer. A nouveau, il lui manque ce supplément d'âme et la prise de risque qui caractérisent l'oeuvre d'art.

Motif aléatoire de 5000 points -
Le chef-d'oeuvre ci-contre, de Picasso, se situe précisément quelque part entre les extrêmes, ni trop simpliste pour lasser, ni trop complexe pour décourager. Il présente des redondances syntaxiques, liées, par exemple, à la similitude de pixels voisins qui peuvent être codés simultanément, mais aussi plus subtilement sémantiques, relatives aux signes distinctifs que notre cerveau a appris à identifier et dont il se sert pour examiner les détails, du visage, des mains, ..., même s'ils sont savamment déformés.

Jacqueline au chapeau jaune
Résumons ce que nous avons appris avant de discuter l'exemple musical :
- Un système aléatoire est incompressible (et incompréhensible car il n'y a rien à comprendre !). La réciproque est également vraie, d'où ces deux notions se recouvrent intégralement.
- Un système non aléatoire est structuré par une logique interne qui rend sa compression possible. Parmi tous les programmes compresseurs envisageables, l'un est forcément plus court que tous les autres. Sa longueur détermine la complexité algorithmique du système (Son entropie, en bits).
- La compression est possible parce que le système est redondant syntaxiquement et sans doute sémantiquement. Tous les observateurs, y compris l'ordinateur, sont égaux devant la redondance syntaxique, qui est de nature statistique, mais pas forcément devant la redondance sémantique. Dans ce dernier cas, l'expérience, la culture personnelle, l'intelligence, ..., s'avèrent déterminantes pour anticiper l'évolution du système, par exemple fluidifier la lecture ou l'écoute. A noter que le test de Shannon, qui contrôle l'anticipation intelligente du texte littéraire ou musical, ne joue aucun rôle en peinture car la dimension temporelle y est absente. Il n'y a rien à anticiper dans un tableau, on le perçoit immédiatement dans sa globalité.
En Musique
La sémiologie classique conteste que la notion de langage soit extensible à la musique. Si l'on exige d'un langage qu'il soit signifiant, cela est correct et nul(le) ne s'est mieux exprimé(e), à ce sujet, que Monique Philonenko dans son essai, Musique et Langage (Revue de métaphysique et de morale, 2/2007 (n° 54), p. 205-219). J'en adapte très librement les arguments suivants (mais je vous invite à lire l'essai entier, 15 pages d'une rare limpidité, ne serait-ce que pour rectifier les libertés que j'aurais prises) :
Langue parlée et Musique ne font pas appel aux mêmes ressources cognitives. La première établit un rapport entre un signifiant et un signifié, ce que la seconde ne fait absolument pas. La musique ne renvoie qu'à elle-même et l'information qu'elle porte n'est absolument pas destinée à faire progresser notre connaissance, d'ailleurs la notion de vérité lui est étrangère. S’il existe des règles que l’on doive suivre dans la composition, elles ne sont pas là pour faire advenir une signification, mais pour susciter une émotion qui, par-delà les mots, se transmet du compositeur à l’interprète et de l’interprète à l’auditeur. La musique ne signifie rien, pas même affectivement : l'andantino de la Sonate D959, de Schubert, sera considéré comme triste, nostalgique, consolateur et même peut-être radieux, selon l'état particulier de celui qui l'écoute, et que la sonate soit en la majeur n'y changera jamais rien. Seule la poésie pourrait, à la rigueur, supporter la comparaison musicale, en raison de l'usage qu'elle fait d'éléments non verbaux, allant jusqu'à libérer la syntaxe pour mieux véhiculer l'émotion.
Cependant le point de vue sémiologique n'est pas tout et le célèbre linguiste, Noam Chomsky, a largement contribué à une généralisation de la notion de langage dans le cadre de l'informatique théorique. La Théorie de l'information, comme on l'appelle aussi, considère qu'un texte n'a pas besoin de signifier quoi que ce soit pour exister, en particulier pour occuper une place en mémoire d'ordinateur. Chomsky a identifié les quatre types d'automates, capables de générer systématiquement des langages (formels) de plus en plus riches, au moyen de grammaires adaptées, qu'il a déclinées dans sa célèbre Hiérarchie. Par exemple, le système formel, discuté au §I, génère des théorèmes mais il peut être réinterprété comme détaillant les mots d'un langage abstrait, notés dans l'alphabet binaire {0,1}.
Dans le cadre de cette généralisation, oui, la musique est un langage parmi d'autres, elle en possède tous les attributs formels : un alphabet, une syntaxe, une grammaire et même une orthographe. De base, l'alphabet est composé de notes, plus un grand nombre de signes de ponctuation (silences, dièses, bémols, etc) destinés à marquer les altérations, durées, rythmes, superpositions, répétitions, etc. Tout texte rédigé sur base de cet alphabet et, on présume, respectant de près ou de loin des règles de Solfège et des principes d'Harmonie et de Contrepoint, peut prétendre au titre de partition musicale. Que celle-ci soit audible est une autre affaire.
L'intelligibilité du texte musical repose, comme celle du texte littéraire, sur un ensemble de redondances syntaxiques et sémantiques. On peut réitérer à son sujet le test de Shannon, ce qui a été fait maintes fois (cf, par exemple, la Thèse de Sarah Culpepper, University of Iowa, 2010). On peut alors revisiter les musiques des 250 dernières années, dans la perspective d'une étude comparative en complexité. Il y a lieu de noter que le test de Shannon concerne l'interprète avant l'auditeur et les exemples abondent, dans l'histoire du concert ou de l'enregistrement, d'oeuvres ne trouvant que tardivement l'interprétation (provisoirement !) idéale, celle qui apporte de bonnes clés de déchiffrage. Bien sûr, toute interprétation respecte la partition et toutes les notes s'y trouvent, ce n'est pas cela qui est en cause, mais, au travers d'une diction réinventée, des redondances se révèlent qui permettent enfin à l'auditeur de (mieux) s'orienter.
En étudiant, de cette façon, la complexité des oeuvres musicales, on retrouve, moyennant les transpositions qui s'imposent, les conclusions propres à l'analyse du texte littéraire (ou de la peinture). Sans redondance, une partition est incompressible donc aléatoire et ingérable par le cerveau humain, celui de l'interprète comme celui de l'auditeur. Trop redondante, elle est banale et ne résiste pas aux écoutes répétées. Toute musique doit trouver un juste équilibre entre ces extrêmes. Les exemples ci-avant, empruntés au monde de la peinture, trouvent leurs équivalents en musique :
- Le pendant musical de la toile blanche existe, c'est 4:33 de John Cage (1912-1992), une partition vierge faisant appel à un pianiste inactif pendant la durée indiquée ! Evidemment, Cage n'était pas dupe du procédé. Il voulait simplement attirer l'attention du public sur ce fait sensoriel que, même lorsqu'on ne joue rien, on continue d'entendre les bruissements ambiants, que nos oreilles contemporaines, constamment agressées, ont appris à gommer. Bien sûr, le procédé est inexploitable, ayant épuisé une fois pour toutes son pouvoir subversif.
- Erik Satie (1866-1925) a fait très fort dans Vexations, une oeuvre non publiée et destinée à être jouée 840 fois de suite (!), ce qui demanderait entre 10 et 20 heures, selon le tempo choisi. Le conditionnel cessa d'être de mise lorsque, de l'autre côté de l'Atlantique, John Cage (encore lui !) tenta l'aventure au cours d'un de ces happenings marathons dont les milieux branchés étaient friands, à l'époque (1963). De nos jours, l'expérience est encore parfois réitérée, en particulier par le pianiste Nicolas Horvath (En juin 2015, à la Maison de la Radio !).
- La musique purement fractale existe mais elle est de faible complexité, à ranger, comme la précédente, au rayon des musiques d'ameublement. Le compositeur danois, Per Norgard (1932- ), a tenté d'insérer des motifs de ce type dans quelques très belles partitions (Symphonie n°2 et Voyage into the Broken Screen) mais le procédé est difficilement repérable par une oreille non exercée du fait que la récurrence s'effectue dans le temps (et non dans l'espace comme c'est le cas des images fractales), ce qui sollicite la mémoire auditive dans un registre qu'elle ne cultive pas. Pour plus de détails techniques, reportez-vous au portrait de Norgard.
- Iannis Xenakis (1922-2001) a suivi une voie lointainement apparentée en expérimentant une programmation mathématique des hauteurs de sons, des rythmes et des timbres. De telles œuvres sont, a priori, de faible complexité puisque réductibles, comme les fractales, au petit ensemble des formules utilisées mais, heureusement, Xenakis n'en est pas resté là : il a superposé des éléments extérieurs de complexité en introduisant un hasard contrôlé, magnifié par une instrumentation extrêmement sophistiquée. Le résultat est particulièrement probant dans Jonchaies, pour 109 instruments.
- La musique vraiment aléatoire, qui tirerait au hasard chaque paramètre du son, n'a aucune chance de survivre, noyant les infortunés auditeurs sous un flot d’informations qu’ils ne pourraient gérer. La différence entre note juste et fausse cesserait d'ailleurs d'exister puisqu'elles seraient interchangeables, ce serait la négation de l'oeuvre d'art. Qui peut raisonnablement adhérer au projet un temps entrepris par John Cage (toujours lui !), alors dans sa période radicale (Music of changes, 1961) ? Il existe cependant des variantes pseudo aléatoires parfaitement écoutables, qui n'abandonnent aux interprètes que des plages d'improvisation mesurées. La réussite historiquement la plus probante du genre est, sans doute, In C (En Ut) de Terry Riley (1935- ), ici précisément en concert à Amsterdam. La partition tient en une seule page de 53 motifs brefs devant être joués, dans un ordre prescrit, par un nombre non précisé d'instrumentistes. Chaque exécutant peut et doit répéter le même motif le nombre de fois qu'il juge opportun avant de passer au motif suivant. Seule l'écoute qu'il reçoit de ses partenaires, forcément déphasés, doit dicter ses choix, le but étant de créer une symbiose différente à chaque exécution. Les pauses sont admises afin de se repositionner régulièrement à bonne distance des partenaires.
- L'essentiel du "grand" répertoire occupe, sans surprise, le domaine des complexités intermédiaires. Note ajoutée en février 2024 : Dans un article paru dans la Phys. Rev. Research 6 (2024), Suman Kulkarni, Sophia U. David, Christopher W. Lynn, et Dani S. Bassett ont développé un modèle en réseau capable d'analyser les transitions de notes dans l'oeuvre de J S Bach. Leurs résultats confirment le point de vue développé ci-avant.
La musique (de l'ère) classique, singulièrement celle de Mozart, offre les exemples canoniques de redondances parfaitement assimilées par tous les publics, au point qu'elle passe pour relativement prévisible (Ceci ne constitue pas un jugement de valeur !). En musique classique, la redondance la plus évidente est la reprise à l'identique d'une section précédemment énoncée, ce qui est fréquent dans un mouvement de forme sonate. Ce procédé, propre à la musique, est parfaitement toléré alors qu'il serait impensable dans un texte littéraire.
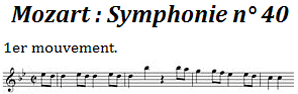
Le recours à une tonalité spécifique est une autre source historique de redondance : un mouvement écrit, disons, en sol mineur, n'utilise que 7 notes sur les 12 qui partitionnent l'octave d'où une compression devient possible, en mettant, une fois pour toutes, deux bémols en évidence à la clé (Cette armure rappelle l'écriture algébrique bien connue, 2(a+b+c+d)=2a+2b+2c+2d, une économie de symboles sur le long terme). Le respect d'une tonalité spécifique crée d'autres redondances qui renforcent la précédente : une note en entraîne souvent une autre de façon plus ou moins prévisible du fait des rapports harmoniques qui existent entre elles et l'auditeur en est conscient même s'il ne connaît rien à la théorie musicale. Ces redondances créent un pouvoir d'anticipation des notes à venir (Le test de Shannon !), jusqu'à ce qu'une cadence provoque une transition inattendue. Elles confèrent à l'auditeur (sans parler de l'interprète !) une sensation de confort qu'il apprécie. A l'opposé, une musique peu redondante est imprévisible et déstabilisante.

La répétition motivique micro-variée est une autre source de redondance dont l'usage a culminé dans l'oeuvre de Beethoven. Le finale de la Symphonie n°7 commence par deux accords brefs, suivis d'un motif de 7 notes répété 24 fois en l'espace de 30 secondes, avec quelques nuances subtiles ! L'œuvre de Beethoven tire largement son pouvoir universel de persuasion de ce procédé rhétorique (Cfr encore le motif bondissant de 4 notes qui ouvre le finale de la Sonate n°17 ). On pourrait certes le juger facile, voire l'assimiler à un tic d'écriture, mais il est tellement bien emballé qu'on s'y laisse prendre à chaque fois. Même les derniers Quatuors du Maître, réputés sans concessions, ont subrepticement recours au même procédé : le début du 2ème mouvement du Quatuor n°15, opus 132, alterne, avec autant de subtilité que d'insistance, des motifs de 3 et 6 notes (commence en 10:35).
La disparition de Beethoven (et n'oublions pas Schubert, qui l'a suivi dans la tombe un an plus tard), en 1827, a laissé un vide dans la musique germanique alors en position dominante. Deux écoles se sont partagées la succession, celle classique, dirigée par Felix Mendelssohn (1809-1847), et celle, progressiste, dirigée par Franz Liszt (1811-1886). On crédite généralement Liszt d'avoir envisagé une musique de l'avenir. L'idée a été de s'affranchir progressivement du carcan de la tonalité en multipliant les altérations, ce qui diminue d'autant la redondance du texte. A la limite, lorsque les altérations deviennent trop nombreuses, il ne sert plus à rien de mettre des dièses ou des bémols à la clé : on entre de plain-pied dans un chromatisme généralisé à 12 sons par octave, menant tout droit à l'atonalité. Son œuvre la plus étonnante, à cet égard, est sans doute la Bagatelle sans tonalité, dont le titre est éloquent.
L'atonalité a également fait une (timide) apparition dans The unanswered Question, de Charles Ives (1874-1954). Cette pièce est construite sur trois niveaux : des cordes jouent, sans arrêt, les mêmes triades en sol majeur (bel exemple de compressibilité !) mais elles sont régulièrement interrompues par une trompette hors tonalité. C'est la fameuse "question" à laquelle un quatuor de bois tente vainement de répondre, sur un ton de plus en plus dissonant. Leonard Bernstein a magistralement analysé cette œuvre emblématique de la musique américaine naissante dans la Leçon 5 de ses incontournables Six Norton Lectures in Harvard (1973).
Il a cependant fallu attendre Arnold Schönberg (1874-1951) pour que la redondance tonale soit systématiquement remise en question. Après une période d'atonalité libre (Drei Klavierstücke, opus 11, notez l'absence d'armure, sur la partition qui défile), encore ancrée dans une certaine tradition, c'est vers 1920 qu'il a formalisé le principe de la série dodécaphonique, destinée à remplacer le thème cher à la musique classique. Schönberg s'est parfaitement rendu compte qu'en instaurant une démocratie entre les 12 notes de la gamme tempérée et en bannissant toute forme de répétition, il perdait d'office un élément vital de compressibilité syntaxique. Il a compris que l'abandon des anciennes règles en imposait de nouvelles sinon la succession aléatoire des notes menaçait la partition de chaos incompressible. Il a opté pour le principe de la série de 12 sons, assujettissant les développements à toutes sortes de nouvelles règles (Motifs rétrogrades, miroirs, miroirs rétrogrades et leurs conséquences naturelles). Ces règles qui fondent la musique sérielle peuvent paraître arbitraires et elles le sont effectivement mais, au fond, on juge l'arbre à ses fruits et, à cet égard, on se demande pourquoi les Variations pour Orchestre, opus 31, effrayent encore tant d'auditeurs, près de 100 ans après avoir été composées. Schönberg n'était nullement sectaire et il a souvent enfreint les règles qu'il avait lui-même dictées : le premier mouvement de son Quatuor n°3 offre un bel exemple de répétitions s'étendant sur 12 mesures. Ce musicien, pourtant essentiel au 20ème siècle, n'a pas encore convaincu le grand public, qui s'en est toujours tenu à la phrase injustement sévère de Maurice Ravel, "Ce n'est plus de la musique, c'est du laboratoire".
Note sur l'atonalité libre. L'ambition schönbergienne de s'affranchir des repères tonals s'est heurtée à la difficulté suivante : il est de fait aussi difficile d'écrire "de tête" une oeuvre complètement atonale que de positionner "à la main" des points au hasard dans un cadre carré (seul un pseudo-hasard est possible). Des réflexes tonals s'y opposent, qui ont pour conséquence d'incorporer de courts motifs en rapports harmoniques ne produisant, au bilan, qu'une oeuvre pseudo-tonale. Schönberg n'a pas trouvé d'autre issue que d'imposer un ensemble de règles contraignantes, celles qui fondent précisément la musique sérielle. Sa solution n'est cependant pas la seule envisageable (cf infra, une variante due à Hauer).

Beaucoup de compositeurs ont sauté dans le train mis en marche par Schönberg, à commencer par trois de ses élèves, Alban Berg (1885-1935), Hans Erich Apostel (1901-1972) et Anton Webern (1883-1945). Chacun a trouvé sa voie, en particulier au niveau des critères du choix des séries. Sans répétition, il existe 12 ! = 479 001 600 séries dodécaphoniques différentes et certaines (peu nombreuses !) s'avèrent plus consonantes que toutes les autres. On retrouve, à cet égard, tout l'éventail des complexités. Qu'il existe des séries à fort potentiel consonant ne devrait surprendre personne, il suffit d'enchaîner les notes en respectant leurs liens harmoniques. Un bel exemple ouvre la Faust Symphonie de Liszt : l'accord initial est suivi d'une série dodécaphonique avant la lettre, à laquelle l'oreille se laisse prendre du fait qu'elle est organisée par triades successives . A l'opposé, les séries aléatoires (Les 12 sons, tirés au sort !) sont de complexité maximale donc difficilement gérables.
- Berg (Suite lyrique) et Apostel (Adagio pour cordes) ont précisément tenté de préserver une forme de lyrisme dans leurs choix de séries et les oeuvres mentionnées pourraient vous convaincre.
- Webern (Symphonie, opus 21) s'est montré nettement plus radical, privilégiant des séries erratiques, du moins en apparence, mais autorisant un traitement formel cohérent. A noter que cette musique est plus sémantiquement compressible qu'il y paraît : une logique arithmétique interne la structure, que l'auditeur ne peut appréhender que si on la lui enseigne. Cette musique exige donc une préparation que décline généralement le public ordinaire. Il est à craindre que ce problème demeurera éternellement sans solution car nous sommes tous en manque de temps pour progresser dans cette voie. Seule concession à l'auditeur, Webern a volontairement limité chacune de ses partitions à quelques minutes seulement.
- Schönberg a connu un rival, Mathias Hauer (1883-1959), indigné que l'histoire lui ait refusé la paternité de l'atonalité. Ses choix de séries étaient basés un principe nettement restrictif qu'il a appelé "trope" (Une chronique consacrée à ce musicien vous en dit plus à ce sujet). Hauer n'avait pas le génie de Schönberg mais sa musique ne manque pas d'intérêt pour autant. Fait rare en musique atonale, son opéra Salambo propose un chant étonnamment expressif. Quant aux centaines de Zwölftonspiele, ils revendiquent une inexpressivité non dépourvue d'intérêt : Zwölftonspiele pour orchestre, daté de 1957, s'articule autour d'une séquence de 12 accords de 4 notes, répétée en boucle mais présentant, à chaque passage, une altération différente. La pièce donne l'impression d'un continuum sans réel début ni fin, anticipant à sa manière le mouvement minimaliste à venir. C'est une véritable contemplation méditative d'un univers dodécaphonique possible parmi (beaucoup) d'autres.
Pendant la période difficile qui a suivi la deuxième guerre mondiale, le principe de la série a été généralisé à tous les paramètres sonores. Dans leurs œuvres les moins conciliantes, Pierre Boulez (1925-2016) et Karlheinz Stockhausen (1928-2007) ont atteint les limites de la complexité audible.Klavierstücke de Stockhausen est tellement expérimentale qu'elle décourage l'immense majorité des auditeurs, étonnés que l'histoire ait conservé des témoignages d'expériences aussi peu concluantes (Qu'aurait pensé Ravel ?). Sachez qu'il existe un autre Stockhausen, musicien très supérieur à l'expérimentateur : le contraste entre Klavierstücke et Tierkreis, Stimmung (Exigez la version de Copenhague, par l'Ensemble vocal de Paul Hillier) ou le 4ème acte de Samstag aus Licht (Luzifers Abschied) est de fait saisissant.
L'hyper complexité a coûté cher à la musique (post)sérielle : le public l'a tout simplement ignorée. Une réaction était inévitable et la tonalité a refait surface ou plus exactement la modalité. C'est une manière de concevoir la redondance, en restreignant autrement l'ensemble des notes utilisées. La modalité étendue prolonge les modes majeurs et mineurs qui avaient finis par s'imposer en musique classique : elle en considère beaucoup d'autres dont certains d'ailleurs très anciens. Gammes par tons entiers (Debussy), gammes à transpositions limitées (Messiaen), gammes exotiques, Blues, ..., ont ouvert la porte aux brassages postmodernes, typiques de la fin du 20ème siècle.
Le mouvement minimaliste, né aux USA, a clairement souhaité renouer avec un certain confort d'écoute, en restaurant les compressibilités mélodiques et rythmiques. Il ne faut pas se méprendre sur le degré réel de complexité des premières œuvres de Philip Glass(1937- ), très supérieur à ce que l'appellation musique répétitive pourrait laisser entendre : l'extraordinaire Knee Play III, extrait de l'opéra, Einstein on the Beach, est envahi par une prolifération rythmique sans cesse changeante, qui complique la tâche des interprètes. Au bout de deux minutes, la cascade des notes laisse place à un bel épisode planant, puis la séquence complète recommence à l'identique, au bilan une belle synthèse de procédés redondants. Plus récemment, au grand dam des experts mais pas d'un public jeune, Glass a rendu son style nettement plus compressible, en assagissant le rythme et en multipliant les arpèges consonants (The Civil War Acte V, Scène A, Concerto pour violon n°1, ...). Son collègue, Steve Reich (1936- ), a davantage travaillé la complexité rythmique, ce qui a contribué à le maintenir à l'abri des critiques malveillantes (The four Sections). Le minimalisme a fait école en Europe et je vous renvoie aux chroniques dédicacées, particulièrement celles qui concernent l'Estonie (Arvo Pärt, …), la Grande Bretagne (John Taverner, …) et les Pays-Bas (Simeon ten Holt, …). Je me contenterai de rappeler le Canto Ostinato, du dernier cité, qui séduit par la subtile contorsion de ses méandres, aux pouvoirs nettement hypnotiques.
Le courant minimaliste ne pouvait s'éterniser sans risquer l'implosion. Le balancier de l'histoire musicale s'est dès lors tout naturellement remis à osciller dans le sens inverse : John Adams, aux USA, est rapidement devenu le chantre d'une nouvelle complexité ... décomplexée, à 1000 lieues des excès du post sérialisme. Il est aujourd'hui suivi par toute une génération (Guillaume Connesson, ...) dont vous trouverez des échos, sur ce site, dans les chroniques dédicacées à chaque pays.
En conclusion
Pour qu'une musique soit compréhensible, il faut qu'elle soit compressible donc redondante mais cela ne suffit pas. Encore faut-il que cette redondance soit détectable, en temps réel, afin que le cerveau puisse passer, avec succès, le test de Shannon.
- Les compositeurs du courant traditionnaliste, appartenant à la lignée des Bartok, Stravinsky, Prokofiev, Britten, Schostakovitch, Messiaen, Schnittke, ..., ont, chacun à leur manière, veillé à satisfaire ce critère et le public a largement approuvé leurs oeuvres.
- Les compositeurs du courant progressiste ont cultivé une approche beaucoup plus savante où les redondances se sont trouvées de plus en plus cryptées au sein de la partition. Le phénomène a même pris une ampleur déraisonnable lors de l'épisode (post)sériel des années 1950-60. Sans explication préalable, le mélomane ordinaire s'est trouvé désemparé et il ne faut pas s'étonner s'il se soit détourné d'un répertoire qui bousculait à ce point ses habitudes d'écoute. Il n'est même pas sûr que les explications circonstanciées qui auraient pu lui être fournies lui auraient été utiles.
Enfin, qu'il soit clair que si la théorie de l'information éclaire le processus mental du décodage de l'oeuvre d'art, elle ne se prononce pas sur la valeur esthétique de celle-ci, une notion éminemment subjective et peut-être même superflue. Après tout, il n'est nullement certain que l'art doive nécessairement viser la beauté, au sens apollinien du terme. Qu'elle réussisse à libérer les démons intérieurs de leur créateur et à stimuler l'imagination des spectateurs ne serait déjà pas si mal.