Math
Quelques problèmes mathématiques curieux ou amusants
Sommaire
[ afficher ]- Le Problème de Steiner
- L'étonnante équation différentielle de Lee Rubel
- Trois candidats à la roulette russe
- Chute libre sur un centre fixe et oscillateur harmonique : le changement de variables de Sundman
- Poincaré ou Fibonacci ?
- Quaternions
- 1, 2, 4, 8, 16, 31 !, ... et le problème de Moser
- Un problème géométrique élémentaire mais surprenant
- In Memoriam John Horton Conway
- Le principe de la descente finie
- Triangles à côtés entiers dont deux angles sont en rapport entier
- Un puzzle pythagoricien
- Un problème de trigonométrie "diophantienne"
- Le Problème 6 des Olympiades 1988"
Cette section, en construction permanente, présente des questions de mathématiques, exotiques ou amusantes. Pour une présentation encyclopédique mais lumineuse de problèmes complexes, consultez le site de Keith Conrad.
Le Problème de Steiner
Ou comment résoudre un problème variationnel complexe avec de l'eau savonneuse.
L'étonnante équation différentielle de Lee Rubel
Il y a 30 ans déjà, Lee Rubel a publié un résultat étonnant (Bull. Am. Math. Soc. 4, pp345-349 (1981)), présenté ci-dessous de façon informelle. Les détails analytiques sont reportés en annexe (Notebook Mathematica).
Il est bien connu que toute équation différentielle définit une famille de fonctions. Ainsi l'équation linéaire (d'ordre 2 et de degré 1), y''(x) + y(x) = 0, définit la famille des fonctions trigonométriques de base, sinus et cosinus. Pour des raisons de commodité, on a donné un nom aux solutions des équations utiles aux physiciens (et aux autres !) mais qu'il soit bien clair que les autres équations ne sont pas moins respectables : du moment qu'elles ne sont pas sensibles aux conditions initiales, elles définissent d'autres familles de fonctions qui seront peut-être utiles à leur tour. Rubel a trouvé une équation différentielle d'ordre 4 et de degré 7 qui possède une solution approximant, à moins de epsilon près (epsilon aussi petit que l'on veut), n'importe quelle fonction infiniment continûment dérivable ! Certes cette équation n'est pas simple mais il n'empêche que le résultat est surprenant. L'équation s'écrit :
Comment une telle prouesse est-elle possible ? Observons que la fonction exponentielle, y(x)= exp(a x), satisfait l'équation de Rubel et en cherchant bien on en trouverait beaucoup d'autres. Cependant une fonction choisie au hasard, par exemple, y(x) = sin(x), ne la satisfait pas. Ce que le théorème de Rubel affirme c'est qu'il existe un jeu de conditions initiales qui garantit que la solution correspondante est aussi peu distante que l'on veut de la fonction sin(x) ou d'ailleurs de n'importe quelle autre, infiniment continûment dérivable. L'idée est d'approximer la fonction donnée par un modèle adéquat, sur une suite d'intervalles consécutifs, d'autant plus étroits que la précision exigée est grande. Le modèle considéré par Rubel se note :
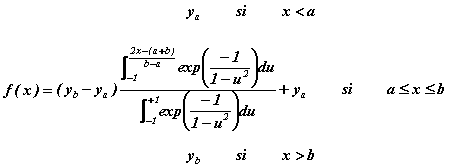
Il est viable parce qu'il possède quelques propriétés remarquables :
- f(a) = ya et f(b) = yb. Autrement dit, le modèle relie, comme souhaité, les points (a, ya) et (b, yb), situés aux extrémités de l'intervalle (a,b).
- f(x) satisfait l'équation de Rubel. Cela est trivial en-dehors de l'intervalle (a,b) puisque le modèle y est constant mais c'est également vrai à l'intérieur.
- Sur l'intervalle (a,b) le modèle s'écarte aussi peu que l'on veut de la fonction donnée, à condition de respecter les limites, f(a)=ya et f(b)=yb, aux extrémités a et b et de rapprocher suffisamment b de a.
- Le raccord du modèle entre deux intervalles consécutifs, (a,b) et (b,c) se fait sans problème grâce aux propriétés remarquables de f(x) : les deux modèles se raccordent, de fait, infiniment continûment au point commun, x=b, car toutes les dérivées y sont nulles.
Si l'un des objectifs de la science consiste à trouver un modèle théorique qui colle à la réalité expérimentale, on constate que l'équation de Rubel apparaît comme universelle au sens où elle rend compte de n'importe quel ensemble de données échantillonnant un phénomène continu. Cependant il faut bien comprendre que cette équation ne possède aucune vertu prédictive dans la mesure où on a déplacé le problème au niveau de la recherche des conditions initiales qui induisent la solution cherchée. Etant donnée une fonction, aucune procédure algorithmique ne peut révéler les conditions initiales à introduire dans l'équation de Rubel afin de calculer la solution qui l'approxime à moins de epsilon près. Cette non-calculabilité limite évidemment l'intérêt de la découverte de Rubel.
On a proposé d'autres équations universelles, plus simples, telles celles de Duffin,
Trois candidats à la roulette russe
Aucun domaine des mathématiques n'est plus délicat que le calcul des probabilités : l'intuition y est régulièrement mise à mal, au point que les pseudo-paradoxes abondent. Celui des tireurs-fous est particulièrement spectaculaire. Trois amateurs de roulette russe (que nous nommerons A, B et C) conviennent d'adhérer au protocole suivant :
- Tous ne sont pas mis sur un pied d'égalité : une roulette indépendante décide de charger le pistolet de A avec la probabilité a, celui de B avec la probabilité, b, et celui de C avec la probabilité, c. On a : 1>a>b>c>0. Les joueurs sont au courant de cette différence et ils l'assument.
- Un autre tirage aléatoire décide d'un ordre immuable parmi les 6 possibilités, ABC, ACB, ..., CBA, et chacun tirera à son tour, dans cet ordre. Si un tireur meurt, les deux survivants continuent à tirer dans l'ordre restant.
- Tout "joueur" peut a priori tirer en l'air ou sur la cible de son choix, sauf qu'il doit impérativement retenir l'option qui lui laisse la meilleure chance de survie. Ensuite, c'est au tour du deuxième joueur de faire pareil et ainsi de suite, jusqu'à épuisement des combattants.
On demande de déterminer la meilleure stratégie de chacun et de calculer les probabilités de survie respectives.
Solution
Une analyse préalable permet de dégrossir le problème : le lecteur se convaincra facilement que la meilleure stratégie, pour A comme pour B (les mieux armés), consiste à tirer sur le rival le plus dangereux (respectivement B et A). Dans tous les cas de figure, on a que la probabilité de survie de A est au moins égale à celle de B, ce qui ne laisse que trois possibilités (on ignore les cas d'égalités en nombres négligeables) : 0 < pc < pb < pa < 1 (cas 1), 0 < pb < pc < pa < 1 (cas 2) et 0 < pb < pa < pc < 1 (cas 3). C'est ce que l'intuition suggère et ce qu'un calcul facile confirme. Par contre, la meilleure stratégie pour C est bien moins évidente : en fait, tant que les trois tireurs sont en vie, C a intérêt à tirer en l'air, ce qui assure que A et B se rencontreront au tour suivant ! Il y a encore plus fort : sous certaines conditions peu contraignantes et relatives aux valeurs de a, b et c, il peut se faire que C possède la meilleure probabilité de survie !
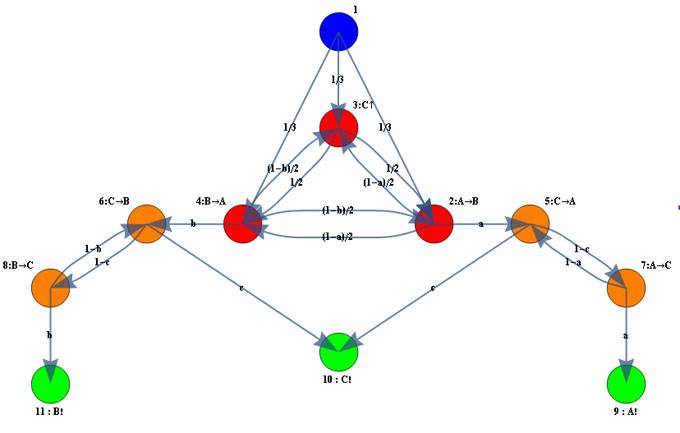
Le graphe de Markov du problème est composé de 11 états, 8 états internes (numérotés de 1 à 8) et de 3 états de bord (numérotés de 9 à 11). Les états internes ont été coloriés différemment selon le nombre de tireurs demeurant en vie à chaque stade. Les états de bord sont absorbants : une fois un de ces état atteint, le système s'arrête, désignant le survivant.
Il existe plusieurs méthodes de résolution d'un tel graphe. La méthode matricielle repose sur les matrices de transition entre états internes, Q8x8=(pi,j), et vers les états de bord, S8x3=(pi,j) :

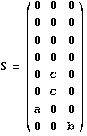
La ligne 1 du produit matriciel, (Id8x8-Q)-1.S, livre les probabilités, pa, pb et pc. Le détail des calculs figure en annexe (Notebook Mathematica).
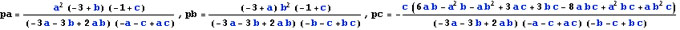
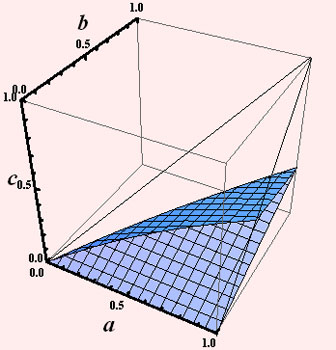
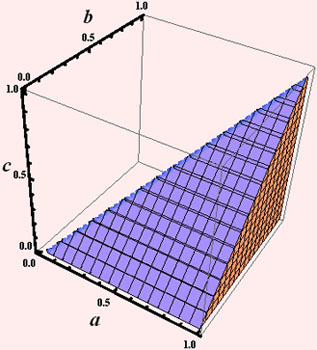
On peut représenter les zones de l'espace 3D correspondant aux trois cas possibles : une figure fixe la portion d'espace tétraédrique disponible, 0 < c < b < a, et l'autre délimite les zones, 1, 2 et 3, dans l'ordre ascendant. On note que la zone 3 (la partie supérieure du tétraèdre) est loin d'être négligeable.
Chute libre sur un centre fixe et oscillateur harmonique : le changement de variables de Sundman
Le problème de la chute d'un corps massif, assimilé à un point matériel, sur un centre attractif ponctuel est classique. L'équation de mouvement est celle de Newton, qui, débarrassée des constantes inutiles, peut s'écrire (le choix opéré des conditions initiales est inessentiel) :
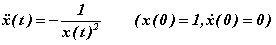
Bien que singulière en x=0, cette équation est intégrable en termes de fonctions élémentaires et sa solution se note, en forme inversée :
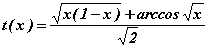
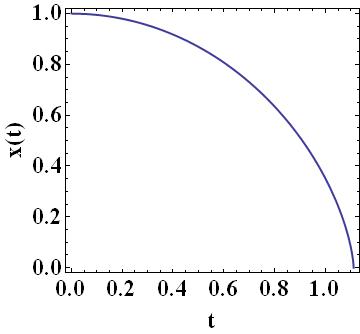
La singularité évoquée correspond clairement à la collision du point avec le centre qui, vu les conditions initiales retenues, se produit en,
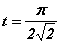
. Une procédure d'intégration numérique se heurte inévitablement à la présence de cette singularité, interdisant toute prolongation numérique de la solution au-delà de cette limite. Cependant Karl Frithiof Sundman (1873-1949) fut le premier à montrer que cette singularité peut être rectifiée, permettant la prolongation sans limite de temps. Physiquement, le point matériel est autorisé à rebondir élastiquement sur le centre ce qui débouche sur un mouvement périodique de période,
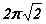
Karl Frithiof Sundman (1873–1949) est un astronome finlandais connu pour avoir effectivement résolu, en 1906-1908, le problème à 3 corps en interaction gravitationnelle. La solution qu'il a trouvée s'exprime sous la forme d'un développement en série uniformément convergent pour toute valeur de la variable temps. Hélas la vitesse de convergence est tellement faible que la série est inexploitable en pratique. L'essentiel du travail de Sundman a consisté à régler le problème des singularités qui lorsque N=3 coïncident avec les collisions (Cette solution a depuis été généralisée aux valeurs supérieures de N par Q. D. Wang).
Le changement de variables de Sundman, (x,t) → (X,T), se note,
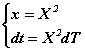
et les calculs s'amorcent comme suit :
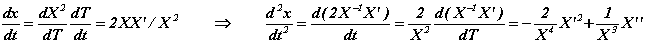
L'équation de Newton pour la chute libre se transforme dès lors en (ne pas confondre la notation pointée qui désigne la dérivée par rapport à t et la primée qui désigne la dérivée par rapport à T; E est l'énergie conservée du point) :
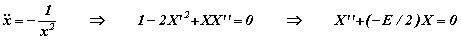
La dernière transformation fait appel à la conservation de l'énergie, traduite en terme des variables X et T, soit : 2 X' 2 - 1 = E X2). Le lecteur intéressé trouvera l'automatisation des calculs en annexe (Notebook Mathematica). On observe que le changement de variables a pour effet d'autoriser le prolongement de la chute libre au-delà de la singularité naturelle que représente la collision avec le centre assimilé à un réflecteur parfait. En terme des nouvelles variables et vu les conditions initiales retenues, le mouvement prolongé est celui d'un oscillateur harmonique, d'équation,
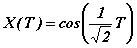
. Il est alors possible de trouver la relation
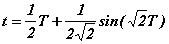
qui relie le temps réel, t, au temps virtuel, T, compte tenu des correspondances initiales,
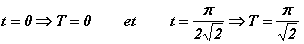
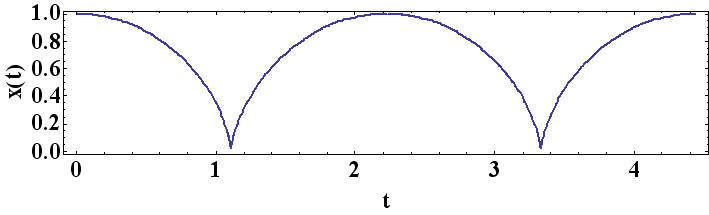
. Le lecteur motivé peut revenir aux coordonnées naturelles par le changement de variables inverse, (X,T) → (x,t), et retrouver la solution, t(x), calculée au début. Le graphe de la solution prolongée se présente comme suit :
Poincaré ou Fibonacci ?
La transformation du chat d'Arnold est fréquemment proposée comme une illustration ludique du théorème du retour de Poincaré. Seuls les bons auteurs font remarquer qu'il n'en est rien car cette transformation illustre avant tout les propriétés de divisibilité des nombres de Fibonacci.
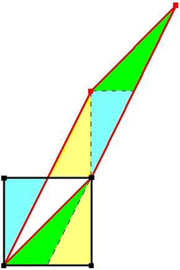
La transformation d'Arnold s'applique aux points du pavé carré de côté, c, qu'elle déforme selon une loi linéaire modulo c,
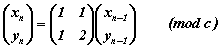
En l'absence du modulo, le carré (contour noir sur la figure) se trouverait déformé en parallélogramme (contour rouge). L'opération modulo a pour effet de découper ce parallélogramme en 4 triangles et de les recoller exactement dans le carré primitif car la transformation préserve les aires. L'opération peut être recommencée autant de fois que l'on veut et on conçoit qu'une image quelconque occupant le carré primitif se trouve progressivement brouillée au point de devenir rapidement méconnaissable. Arnold a le premier fait subir cette transformation à l'image d'un chat d'où son nom.
Une solution analytique est théoriquement possible puisque la transformation est linéaire à un modulo près :
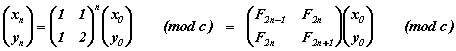
où, Fn = ..., 1, 0, 1, 1, 2, 3, 5, 8, ..., désigne la suite des entiers de Fibonacci (n = ..., -1, 0, 1, 2, 3, 4, 5, 6, ...).
Si on applique la transformation d'Arnold à l'ensemble non dénombrable des points occupant le carré primitif, il devrait être clair qu'aussi loin qu'on réitère l'opération, jamais tous ces points ne reviendront simultanément à leur emplacement initial. En effet, les points pour lesquels une périodicité, N, peut se produire ne constituent qu'un ensemble dénombrable, typiquement celui des solutions (x0, y0), du système,
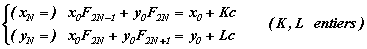
(On trouvera les détails en annexe (Notebook Mathematica)).
Autrement dit, jamais une image de résolution infinie ne réapparaîtra intacte. Une image n'est jamais de résolution infinie et on peut se demander ce qu'il advient d'une image discrétisée selon une grille comptant cxc pixels. Le nombre des cellules élémentaires étant fini (c2) dans ce cas, le nombre total des images possibles est également fini quoique très grand (2cxc). La réapparition de l'image initiale devient, à présent, une certitude programmée dans un temps probablement très grand mais néanmoins fini.
Si l'on expérimente la transformation sur une image initial de taille, c, on observe que le temps de retour est étonnamment court. L'exemple retenu est celui d'une image de la lettre R, discrétisée selon une trame comportant 64x64 pixels : l'image réapparaît au bout de 48 itérations.


Si on rogne l'image en supprimant un cadre extérieur de largeur n, sa dimension s'en trouve réduite à la valeur (64-2n)x(64-2n) : le phénomène de retour précoce subsiste mais le temps de retour change assez irrégulièrement.

Le calcul de la période de retour s'effectue comme précédemment mais cette fois, on impose que les coordonnées, (xn, yn), appartiennent en permanence (= pour tout n) à l'ensemble discret, {0, 1, 2, ..., c-1) :
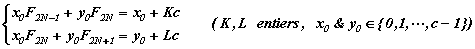
La période cherchée vaut alors la plus petite valeur de N telle que F2N = 0 (mod c) & F2N-1 = 1 (mod c). Le lecteur curieux vérifiera la validité de cette règle, publiée par Freeman Dyson et Harold Falk dans la revue, The American Mathematical Monthly 99 (1992) 603-614, sur les 6 exemples numériques proposés ou il se reportera à l'annexe.
De nombreux auteurs ont voulu voir dans cette expérience numérique une illustration du théorème du retour de Poincaré. Rappelons brièvement en quoi il consiste : un système dynamique instable dont le point représentatif évolue dans un espace des phases borné, y suit une trajectoire chaotique : deux trajectoires initialement proches subissent une divergence localement exponentielle et des repliements successifs qui les séparent définitivement. Toutefois si on découpe l'espace des phases en cellules même microscopiques, un moment viendra où la trajectoire repassera par la même configuration locale, autrement dit, à condition d'être patient le système finira par repasser aussi près que l'on veut de sa configuration de départ. Toutefois cette éventualité ne se produira qu'auterme d'un temps extraordinairement long, sans commune mesure avec ce qu'on observe dans le cas des images discrétisées. Celui-ci est, en fait, la conséquence des propriétés remarquables de divisibilté des entiers de Fibonacci.
Quaternions
Les quaternions sont nés, vers 1843, de l'imagination de Sir William Rowan Hamilton (1805-1865), mathématicien, physicien et astronome irlandais. Considérés d'emblée comme une généralisation des nombres réels et complexes, ils ont été préconisés et réellement utilisés dans une formalisation des équations de la mécanique de Newton et de l'électromagnétisme de Maxwell, jusqu'à ce que le calcul vectoriel les remplace (définitivement ?), au début du 20ème siècle. Aujourd'hui les quaternions refont surface dans des domaines particuliers où leur algèbre concise apporte un vrai confort d'utilisation (Gestion des rotations dans le traitement des images 3D, électromagnétisme et mécanique quantique relativiste).
Une théorie modernisée situe actuellement les quaternions parmi une infinité d'algèbres hypercomplexes, de dimensions croissantes, par exemple dans le cadre de la chaîne de Cayley-Dickson. Celle-ci développe une généralisation de la notion de nombre réel en procédant par récurrence au départ de l'ensemble des réels, muni des règles usuelles d'addition et de multiplication. On y ajoute simplement une notion de conjugaison telle que le conjugué d'un réel est égal à lui-même : Conj[a] = a. Les réels constituent la base de la construction, que l'on pourrait appeler nombres hypercomplexes de rang zéro (K=0). Ayant défini les hypercomplexes de rang, K, par exemple, A, B, C et D, on définit les hypercomplexes de rang (K+1), X et Y, comme des couples ordonnés d'hypercomplexes de rang K, X = {A, B} et Y = {C, D}, entre lesquels on définit les règles suivantes d'addition, de multiplication et de conjugaison :
- Addition : X+Y = {A, B} + {C, D} = {A+C, B+D}.
- Multiplication : X Y = {A, B} {C, D} = {A C-Conj[D] B, D A+B Conj[C]}.
- Conjugaison : Conj[X] = Conj[{A, B}] = {Conj[A], -B}.
La construction progresse comme suit, en respectant ces règles (On trouvera les calculs explicites en annexe (Notebook Mathematica)) :
- On part de l'ensemble usuel des nombres réels, notés a, b, ... .
- Première étape : les nombres complexes. On définit un nombre complexe, z, comme un couple ordonné de réels : z = {a1, a2}. Son conjugué se note, Conj[z] = {a1, -a2}. Comme annoncé, la somme de deux complexes, {a1, a2}+{b1, b2}, vaut simplement, {a1+b1, a2+b2} et le produit vaut, {a1, a2} {b1, b2} = {a1b1-a2b2, a1b2+a2b1}. On utilise habituellement une notation algébrique alternative (mais équivalente), z = e a1+i a2, où les deux clés, e=1 et i=√-1, respectent la table de multiplication suivante :

- Deuxième étape : les quaternions. On définit un quaternion, q, comme un couple ordonné de complexes : q = {{a1, a2}, {a3, a4}}. Son conjugué se note, conformément à la définition générale, Conj[q] = {{a1, -a2}, -{a3, a4}}. La somme de deux quaternions est à nouveau triviale et le produit est détaillé en annexe. On utilise habituellement une notation algébrique alternative (mais équivalente), q = e a1+i a2+j a3+k a4, où les clés, e=1, i, j et k, respectent la table de multiplication suivante :

- Troisième étape : les octonions. On définit un octonion, 𝒪, comme un couple ordonné de quaternions : 𝒪 = {{{a1, a2}, {a3, a4}}, {{a5, a6}, {a7, a8}}}. Son conjugué se note, conformément à la définition générale, Conj[𝒪] = {{{a1,-a2}, -{a3, a4}}, {-{a5, a6}, -{a7, a8}}}. La somme de deux quaternions est à nouveau triviale et le produit est détaillé en annexe. On utilise habituellement une notation algébrique alternative (mais équivalente), 𝒪 = e a1+i a2+j a3+k a4+l a5+m a6+n a7+p a8, où les clés, e=1, i, j, k, l, m, n et p, respectent la table de multiplication suivante :

On voit que cette construction double, à chaque étape, la dimension de l'espace utilisé. L'étape suivante définirait les sédénions à 16 composantes dont on ne fait aucun usage concret, du moins en physique. Ces algèbres ne sont pas de qualités égales, perdant une propriété à chaque étape de la construction : complexes (pertes de l'autoconjugaison et de la notion de comparaison <>), quaternions (perte de la commutativité de la multiplication), octonions (perte de l'associativité de la multiplication), etc.
1) Application des quaternions aux rotations 3D
Les quaternions proprement dits, q = e a1+i a2+j a3+k a4, (présup)posent que les coefficients, a1, ..., a4, sont réels. Cela permet de leur associer une norme, ||q|| (positive), via la relation : ||q||2 = q Conj[q] = a12+a22+a32+a42. Ils apparaissent naturellement en géométrie à 3 dimensions sous la forme particulière, purement vectorielle, i ax+j ay+k az, où (ax, ay, az) représentent les composantes cartésiennes du vecteur a. C'est sans doute cette observation qui a motivé le remplacement du calcul quaternionique par le calcul vectoriel, à la fin du 19ème siècle. Pourtant le caractère purement algébrique du calcul quaternionique lui conserve des vertus incontestables, par exemple dans le traitement des rotations dans l'espace 3D. On commence par un détour utile en évoquant brièvement une théorie des fonctions d'une variable quaternionique calquée sur celle, usuelle, des fonctions d'une variable complexe. La fonction exponentielle, exp[q] = exp[e a1+ i a2+ j a3+ k a4], est particulièrement intéressante. En se rappelant sa définition sous forme de développement en série, exp[q] = Sum[qn/n!, {n,0,∞}], on trouve, après quelques calculs faisant un large usage de l'identité, (i a2+ j a3+ k a4)2 = -(a22+a32+a42) = -α2 :
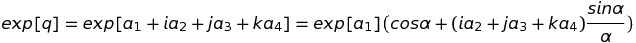
Un cas intéressant apparaît lorsque q est privé de sa partie scalaire (a1 = 0) et que (a2, a3, a4) sont les composantes d'un vecteur unitaire, N = (nx, ny, nz). α valant 1, dans ce cas, la formule précédente se réduit à :
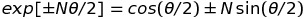
On trouve alors que le double produit suivant transforme un vecteur de composantes (vx, vy, vz) en un vecteur (v'x, v'y, v'z) tourné en sens inverse d'un angle θ autour du vecteur unitaire (nx, ny, nz) :
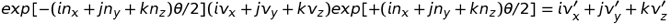
Posant par exemple, nx = ny = 0, nz = 1 et θ = π/4, dans cette formule, on trouve que les produits suivants transforment effectivement i en -j, j en i et k en lui-même :
- (√2/2)(1-k) i (√2/2)(1+k) = -j
- (√2/2)(1-k) j (√2/2)(1+k) = +i
- (√2/2)(1-k) k (√2/2)(1+k) = +k
On trouvera en annexe un autre exemple d'une pyramide ayant subi une rotation de ce genre.
2) Application des quaternions à l'invariance des équations de Maxwell
Rien ne s'oppose à ce qu'on considère le cas plus général où certains coefficients des quaternions sont complexes, on parle alors de biquaternions. Une précaution doit cependant être prise afin de ne pas confondre la clé i des complexes avec celle des quaternions. Dans ce but, on note ci-après la clé des complexes sous la forme parlante, i=√-1.
En physique (relativiste), on distingue deux structures (bi)quaternioniques principales, correspondant respectivement aux quadrivecteurs et aux tenseurs de la théorie usuelle :
- La première regroupe, la position spatio-temporelle d'un événement, R = √-1 c t + i x + j y + kz, le potentiel électromagnétique, P = √-1 V/c + i Ax + j Ay + k Az et le courant, C = μ0 (√-1 c ρ + i Ix + j Iy + k Iz). On note que la partie scalaire est imaginaire pure et la partie vectorielle est réelle. Dans le cas unusuel où l'on souhaiterait "compléter" les équations de Maxwell par la présence de pôles (et de courants) magnétiques, rien ne changerait sauf l'écriture du courant qui revêterait la forme quaternionique généralisée, C = μ0 [(-ρm+ √-1 c ρe) + i (Ie,x+ √-1 Im,x /c) + j (Ie,y+ √-1 Im,y /c) + k (Ie,z+ √-1 Im,z /c)]. La convention d'Ampère a été retenue où les pôles isolés et au repos s'attirent ou se repoussent selon la loi, F = μ0/(4π) qmq'm /r2; ils se mesurent en Am.
- La deuxième s'adresse essentiellement au champ électromagnétique, F = i (√-1 Ex/c - Bx) + j (√-1 Ey/c - By) + k (√-1 Ez/c - Bz). On note que la partie scalaire est absente et que la partie vectorielle est complexe.
De même qu'il ne suffit pas, en calcul tensoriel, d'associer 4 grandeurs pour constituer un quadrivecteur, il ne suffit pas de les assembler au sein d'un (bi)quaternion; il faut encore que les composantes se transforment correctement lors d'un changement de coordonnées, par exemple suite à une rotation des axes ou à une transformation de Lorentz.
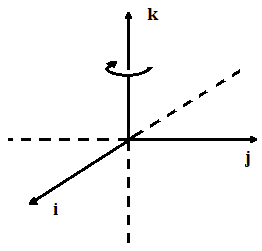
- Lors d'une rotation directe des axes, d'un angle θ, disons autour de Oz pour ne pas compliquer, tous les biquaternions, qu'ils soient du premier groupe (R, P ou C) ou du deuxième (F), se transforment selon la loi du type, R' = exp[kθ/2] R exp[-kθ/2].
- Lors d'une transformation de Lorentz à vitesse relative, v, disons selon Oz pour ne pas compliquer, les biquaternions du premier groupe (R, P ou C) se transforment selon la loi du type, R' = exp[-kφ] R exp[-kφ] tandis que ceux du deuxième groupe (F) se transforment selon la loi du type, F' = exp[kφ] F exp[-kφ]. Ces lois sont conformes aux transformations usuelles, par exemple celles relatives aux coordonnées spatio-temporelles :
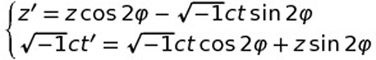
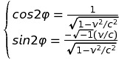
L'écriture des équations de Maxwell requiert l'intervention de l'opérateur différentiel (bi)quaternionique, nabla, ∇ = √-1/c ∂t + i ∂x + j ∂y + k ∂z et de son conjugué, ∇- = √-1/c ∂t - i ∂x - j ∂y - k ∂z. Les lois de transformation pour ce nabla se notent, ∇' = exp[kθ/2] ∇ exp[-kθ/2] (idem pour ∇-), dans le cas des rotations spatiales, et ∇' = exp[kφ] ∇ exp[kφ] (mais ∇'- = exp[-kφ] ∇- exp[-kφ]), dans le cas des transformations pures de Lorentz.
On commence par dériver le champ, F, du potentiel, P, puis on condense les 8 équations scalaires de Maxwell en une seule :
- F = - ∇P
- ∇-F = C
L'invariance des ces relations se démontre aisément en effectuant les transformations suivantes :
- Dans le cas des rotations 3D, la loi de transformation est la même quel que soit le type de quaternion, Q, considéré (type quadrivecteur, position, R = √-1 c t + i x + j y + kz, nabla, ∇ ou son conjugué ∇-, potentiel, P, courant, C, ou champ, F). Elle s'écrit (pour une rotation en sens direct d'un angle θ autour de Oz) : Q' = exp(kθ/2) Q exp(-kθ/2). L'invariance annoncée résulte des enchaînements évidents suivants : 1) F' = - ∇'P' ⇒ exp(kθ/2) F exp(-kθ/2) = - exp(kθ/2) ∇ exp(-kθ/2) exp(kθ/2) P exp(-kθ/2), d'où F = - ∇P, après simplifications, et 2) ∇'-F' = C' ⇒ exp(kθ/2) ∇- exp(-kθ/2) exp(kθ/2) F exp(-kθ/2) = exp(kθ/2) C exp(-kθ/2), d'où ∇-F = C, après simplification.
- Dans le cas d'une transformation de Lorentz proprement dite (selon Oz pour simplifier), l'invariance résulte des enchaînements suivants : 1) F' = - ∇'P' ⇒ exp(kφ) F exp(-kφ) = - exp(kφ) ∇ exp(kφ) exp(-kφ) P exp(-kφ), d'où F = - ∇P, après simplifications, et 2) ∇'-F' = C' ⇒ exp(-kφ) ∇- exp(-kφ) exp(kφ) F exp(-kφ) = exp(-kφ) C exp(-kφ), donc après simplifications, ∇-F = C.
Remarque finale : bien que l'on se soit contenté de cas particuliers (rotation autour du seul axe Oz et translation lorentzienne selon le même axe), les lois de transformations énoncées sont plus générales : il suffit de remplacer le quaternion, k, par N = i nx+j ny+k nz, pour que l'axe Oz soit remplacé par l'axe défini par la direction de N.
1, 2, 4, 8, 16, 31 !, ... et le problème de Moser
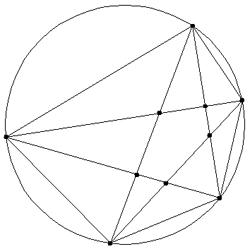
Le problème de Moser dispose m points au hasard sur le périmètre d'un cercle et il trace les m(m-1)/2 cordes possibles. Il pose alors les questions suivantes : combien la figure dessine-t-elle de sommets d'intersection, d'arêtes entre les sommets (y compris les arcs circulaires) et de (sur)faces élémentaires (y compris les secteurs circulaires) ? Ce problème illustre de façon amusante un problème connu d'extrapolation.
1) Les amateurs de soi-disant tests d'intelligence sont férus de questions demandant de compléter une suite donnée d'entiers. Les concepteurs ont une idée logique en tête et entendent récompenser ceux qui vont y adhérer spontanément. C'est ainsi que la séquence, 1, 2, 4, 8, 16, est présumée appeler la suite "naturelle", 32, 64, 128, ..., au motif qu'elle énumère les puissances successives de 2. Au fond, l'interrogateur attend que le candidat propose un programme (au sens informatique du terme) capable non seulement de restituer la séquence donnée mais encore de l'extrapoler dans le sens qu'il a présupposé. Dans l'exemple considéré, le programme attendu pourrait s'écrire simplement dans le langage informatique de votre choix, s1 = 1, sn = 2sn-1 (n = 2, 3, 4, ...).
2) Les esprits critiques ont pourtant beau jeu de faire remarquer que le problème est certainement mal posé et qu'il est facile de proposer d'autres programmes (en fait une infinité) restituant la séquence donnée mais l'extrapolant différemment, par exemple sous la forme, sm = 1, 2, 4, 8, 16, 31, 57, 99, ... (m = 1, 2, 3, ...) ou n'importe quelle autre de votre choix. On s'en convainc aisément en se donnant une formule d'extrapolation, f(m), comprenant autant de paramètres que de valeurs données (5 dans l'exemple) puis en cherchant quelles valeurs il convient de donner à ces paramètres pour que l'on ait, f(m) = sm, pour m = 1, 2, ..., 5. Un modèle simple possible est polynomial, f(m) = c0 + c1 m + c2 m2 + ... + c4 m4 et il exige de résoudre un système linéaire de 5 équations, f(m) = sm = 2m-1, à 5 inconnues, les c0, ..., c4. Le calcul (un brin fastidieux s'il est fait à la main) est détaillé en annexe (Notebook Mathematica) : il livre la formule d'extrapolation, f(m) = 1-3m/4+23m2/24-m3/4+m4/24. On vérifie sans peine que f(m) prend successivement les valeurs, sm = 1, 2, 4, 8, 16, 31, 57, 99, en accord avec les 5 premières valeurs données. Un autre modèle, par exemple inversement polynomial, fonctionnerait de la même façon, extrapolant la suite de départ, 1, 2, 4, 8, 16, de toute autre façon. Il n'y a pas de limite à la fantaisie extrapolatoire.
3) Il est pourtant possible de conférer un sens au problème posé en entrée, à condition de préciser un point. La (bonne) question n'est pas "Extrapolez 1, 2, 4, 8, 16" mais pourrait être "Ecrivez le programme le plus concis qui reproduit la suite, 1, 2, 4, 8, 16, dans le langage usuel de votre choix et voyez comment il poursuit l'énumération. Le programme énoncé précédemment, s1 = 1, sn = 2sn-1 (n = 2, 3, 4, ...), est tellement concis qu'on ne voit pas le moyen de faire plus court, c'est en cela qu'il justifie les attentes du concepteur du test. La longueur du programme le plus court qui imprime une suite après calculs définit la complexité de la suite au sens de Kolmogorov (Pour plus de détails, reportez-vous aux leçons sur la Théorie classique de l'information). C'est dans le cadre de la théorie de l'information que l'extrapolation "attendue", 1, 2, 4, 8, 16, 32, 64, 128, ... prend tout son sens.
Retour au problème de Moser
Le lecteur a compris que tout début de suite pouvait être prolongé algorithmiquement de façon tellement arbitraire qu'il est illusoire, dans la plupart des cas, d'espérer rencontrer une suite prolongée artificiellement dans un problème concret. Le problème de Moser évoqué en introduction est pourtant un exemple célèbre. Les figures suivantes illustrent la géométrie du problème dans les cas simples, m = 1, 2, 3, ..., 7, où les points extérieurs ont été ajoutés un à un au hasard sur les bords du cercle (Le fait de positionner les points au hasard sur le cercle garantit, avec la probabilité 1, que trois cordes ne sont jamais concourantes. Si ce cas se produisait, la figure dégénèrerait et ne conviendrait plus à l'illustration attendue).
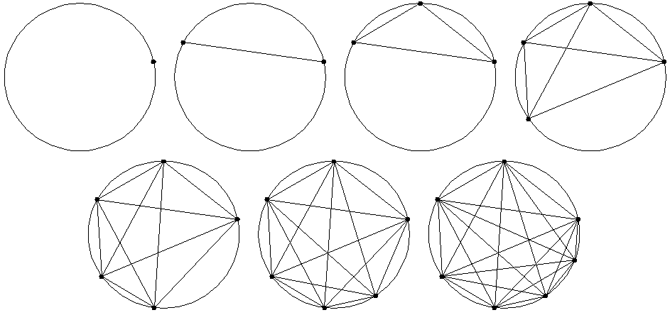
Sur chacune de ces figures on peut vérifier la validité des dénombrements suivants. Lorsque m points extérieurs sont présents sur les bords du cercle, on dénombre :
- m(m-1)/2 cordes. En effet, chaque point lance une corde vers ses m-1 voisins et au bilan elles sont comptées deux fois.
- Cm4 = m(m-1)(m-2)(m-3)/24 sommets (= points) intérieurs. En effet, chaque sommet intérieur se trouve nécessairement à l'intersection de deux cordes définies par 4 points extérieurs; toutes les combinaisons sont distinctes et ne laissent aucun point ignoré. Il y a donc autant de points intérieurs que de façons de combiner m points 4 à 4. Si l'on comptabilise ensemble les sommets intérieurs et extérieurs, ils sont donc en nombre, S = m + Cm4.
- 2Cm4 + m(m+1)/2 arêtes joignant les points voisins (intérieurs ou extérieurs), y compris les arcs de cercle. En effet, de chaque point intérieur émanent 4 segments rectilignes et de chaque point extérieur émanent m-1 segments rectilignes (un par corde émanant de ce point). Au total, chaque segment rectiligne étant compté deux fois, leur nombre total vaut : 2Cm4 + m(m-1)/2. Si l'on inclut les m arcs de cercles entre points extérieurs voisins, on trouve un nombre d'arêtes valant, A = 2Cm4 + m(m+1)/2.
- Cm4 + Cm2 + 1 (sur)faces (élémentaires), celles-ci étant définies comme étant les portions d'aires comprises entre les arêtes adjacentes, y compris les m secteurs circulaires périphériques. Ce calcul fait appel à un cousin du théorème d'Euler, qui relie les nombres d'arêtes, de sommets et de faces de tout polyèdre convexe (par la relation universelle, S+F-A=2). Dans le problème plan qui nous occupe, la relation correcte s'écrit plutôt, S+F-A=1. On démontre celle-ci à partir de celle-là en partant de n'importe quelle figure de Moser, supposée parfaitement élastique, et en la déformant pour la faire sortir du plan de manière à reconstituer un polyèdre dont une seule face serait manquante (Celle qui correspondrait au périmètre déformé du cercle). Une démonstration directe par récurrence est également possible en démontant progressivement la figure de Moser par extractions successives d'une arête. Deux cas sont en effet possibles : 1) A et F diminuent d'une unité et S reste intact ou 2) A et S diminuent d'une unité et F reste intact mais dans tous les cas, S+F-A demeure constant. Lorsqu'il ne reste plus qu'une seule arête, S=2, F=0 et A=1, donc la constante ne peut valoir que 1. Le nombre de faces, F, se déduit donc du nombre des arêtes et des sommets et on trouve bien, F = Cm4 + Cm2 + 1.
Le nombre des faces s'écrit encore, en développant l'expression précédente, F = m(m-1)(m-2)(m-3)/24 + m(m-1)/2 +1, un polynôme de degré 4. On ne peut que retrouver le polynôme d'interpolation de degré 4 trouvé en introduction et de fait, on vérifie que l'on a bien, F = 1-3m/4+23m2/24-m3/4+m4/24.
Pour ceux qui veulent comprendre par quelle coïncidence 5 puissances successives de 2 interviennent dans l'inventaire des (Cm4 + Cm2 + 1) faces (pour m = 1, 2, 3, 4, 5), le plus simple est d'observer que les grandeurs, 1, Cm2 et Cm4, occupent les diagonales n°1, 3 et 5 du fameux triangle (symétrique) de Pascal, dont les lignes totalisent notoirement les puissances successives de 2. Les éléments intéressants pour le problème de Moser ont été imprimés en rouge pour faciliter les sommations. On voit qu'à partir de la 6ème ligne, le total vaut 31 et non 32 : on s'écarte inexorablement de la puissance de 2 naïvement espérée.

Un problème géométrique élémentaire mais surprenant
Le problème suivant est a priori élémentaire et cependant si on procède à un sondage (en famille, à l'école, ...) en vue de collecter les réponses possibles, obtenues sans effectuer le moindre calcul mais en exerçant simplement son intuition, on se trouve confronté à une grande disparité de résultats. Le problème pourrait avantageusement être discuté en classe : il permettrait à des élèves de 14-15 ans de récapituler de façon ludique quelques notions qu'ils peinent éventuellement à assimiler. L'énoncé est le suivant :
- On considère un terrain de football de 100 m de long. On tend une corde souple mais inextensible, longue de 100 m, entre les lignes de but et on la fixe à ses extrémités. La surface du terrain étant supposée plane, la corde est forcément parfaitement rectiligne, rien de particulier à ce stade.
- Si on allonge la corde d'un mètre, sans toucher à ses extrémités qui demeurent fixées, elle mesure à présent 101 m et elle cesse d'être parfaitement rectiligne, lézardant sans doute un (petit) peu. Il est à présent possible de saisir la corde entre le pouce et l'index, soit en son milieu soit quelque part près d'une extrémité de telles manières que, tendue à la verticale de la ligne médiane (cas 1) ou de celle de but (cas 2), elle dessine l'un ou l'autre des motifs représentés ci-après en vue de profil (Pas forcément à l'échelle !).
- La question posée est : pouvez-vous estimer (deviner), à l'intuition seulement, l'ordre de grandeur de la hauteur, h, que la corde atteint dans les deux cas de figure envisagés ? Personne ne se trompe dans le cas n°2 : de fait la portion oblique de corde mesurant visiblement un peu plus de 100 m, la portion verticale (précisément égale à h) ne peut qu'être légèrement inférieure à 1 m, la valeur exacte ne pouvant résulter que d'un calcul détaillé qui n'est pas demandé à ce stade. Il n'en va pas de même dans le cas n°1 : faites un sondage autour de vous, vous récolterez probablement des avis divergents, compris entre 20 cm et 4 m (voire davantage mais avec une concentration nette en-dessous d'un mètre).
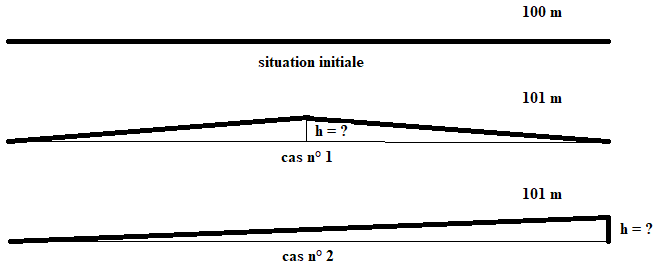
(Echelle non nécessairement respectée !)
Pour contrôler les résultats exacts dans chaque cas, un calcul s'impose qui est à la portée de n'importe quel collégien au fait du théorème de Pythagore et capable de mettre un système en équations puis de le résoudre. Tant qu'à faire, effectuons le calcul dans le cas général où la corde est pincée en un point quelconque et épouse le profil final suivant :

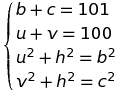
Les contraintes géométriques et l'application répétée du théorème de Pythagore aux deux triangles rectangles de la figure précédente imposent le système ci-contre, duquel il convient de tirer h en fonction de u. Soustrayant membre à membre les équations 3 et 4 donne immédiatement : v2 - u2 = c2 - b2, soit encore, 100(v-u) = 101(c-b). En combinant cette équation avec b+c=101, on a ce qu'il faut pour tirer b (et c) en fonction de u. On trouve par exemple (et cela suffit) : b = 101/2 - 100/101 (50-u). En introduisant ce résultat dans la troisième équation, on trouve la réponse souhaitée sous la forme : h2 = [101/2 - (100/101)(50-u)]2 - u2, soit finalement :

On détaille aisément les deux cas proposés :
- Cas 2 (u=100 et v=0 ou, ce qui revient au même, u=0 et v=100) : h = 50.5 - 5000/101 = 201/202 = 0.995 m. Aviez-vous prédit d'être si proche de 1 m ?
- Cas 1 (u = v = 50) : h2 = 201/4, d'où h = 7.088 m !
On peut représenter graphiquement la solution, dans le cas général, en affichant la hauteur, h, atteinte selon la valeur de u. La courbe dessinée est manifestement le lieu des points dont la somme des distances aux points fixes de coordonnées (u, h) = (0, 0) et (100, 0) est constante, en effet b+c=101; c'est donc une ellipse très aplatie dont les foyers sont précisément situés en ces points (Ne vous fiez pas aux échelles du graphique, en u et en h, qui sont très différentes !).
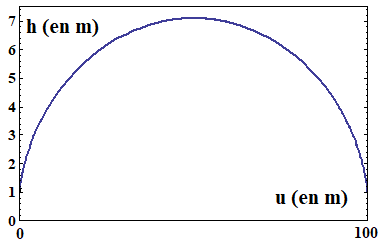
Il est facile de voir que la formule trouvée ci-dessus, b = 101/2 - 100/101 (50-u), est équivalente à l'équation de cette ellipse en coordonnées polaires, (b, θ). Il suffit de noter sur la figure générale précédente que l'angle θ est tel que u = b cos(θ). En faisant le remplacement, on trouve alors, après simplifications, l'équation polaire d'une ellipse de distance focale, FF' = 100, et d'excentricité, e = 100/101 :


On note que le grand axe excède légèrement 100 m, précisément 101 m, valeur calculée d'après la valeur de b = 201/2, en θ = 0. C'était prévisible puisque cela correspond à l'étalement de la corde tendue horizontalement en arrière de l'un quelconque des deux buts.
Parvenu à ce stade, on aperçoit une méthode d'estimation mentale directe de la hauteur h atteinte par la corde tendue à la verticale du milieu du terrain. Le cosinus de l'angle θ vaut clairement 50/50.5 = 100/101, dans ce cas. Pour trouver h, on a besoin de la tangente de θ (car h = 50 tgθ). Or celle-ci est reliée au cosinus par la formule classique, 1 + tg2θ = 1/cos2θ. L'inverse du cosinus valant exactement 1.01, son carré vaut 1.02 avec une excellente approximation donc tg2θ est (très) proche de 2/100 et tgθ est également proche de ✓2/10 = 0.141. Au bilan 2h est proche de 14.1 donc h de 7.05. Dans ce cas précis, il n'y a sans doute pas moyen de faire plus court dans l'estimation de h.
In memoriam John Horton Conway (1937-2020)

Le Covid19 a eu raison de John Horton Conway, l'un des mathématiciens les plus remarquables de notre temps. Il a fait des recherches dans divers domaines des mathématiques, Théorie des Groupes, Géométrie topologique, Automates cellulaires, Algorithmique, etc, mais le point remarquable qui l'a distingué de la plupart de ses collègues, c'est qu'il a tenté de mettre ses résultats à la portée du plus grand nombre toutes les fois que cela s'est avéré possible. Il s'est montré particulièrement habile pour déconstruire des théories complexes, parfois abstraites, et leur trouver des illustrations ludiques dans le domaine prisé des mathématiques récréationnelles (Cf : E. R. Berlekamp, J. H. Conway and R. K. Guy, Winning Ways for Your Mathematical Plays, A K Peters/CRC Press; 2nd edition, 2004) :
- Il a fait fortune intellectuelle auprès des amateurs distingués en concevant le plus célèbre des automates cellulaires, désormais connu sous le nom de Jeu de la Vie (Vous trouverez les règles simples du jeu à cette adresse). Cet automate a ultérieurement été démontré équivalent à une machine de Turing universelle, c'est-à-dire capable de calculer tout ce qui est calculable sous réserve d'un codage adéquat. Avec le temps, une communauté active s'est développée à laquelle n'importe quel amateur (doué !) peut contribuer (Voici un exemple qui propose simultanément plusieurs sous-structures aux comportements caractéristiques : invariantes, périodiques, mobiles, etc). Pour vous donner une idée des prouesses réalisées en matière de codage, visitez le musée des oscillateurs connus, c'est à dire des structures qui se répètent périodiquement en suivant les règles prescrites par Conway.
- Il a récidivé avec son langage minimaliste Fractran évoqué ailleurs sur ce site.
- Vous trouverez encore sur ce site son algorithme de résolution du problème des 12, 39, 120, ..., boules, celui du calcul de la date de Pâques ou encore, ci-après, cette méthode simplifiée du calcul du jour correspondant à une date donnée.
Le problème posé est lié à celui de la construction d'un calendrier perpétuel (grégorien, celui que nous utilisons actuellement). Pour rappel, le calendrier grégorien (Du nom du pape de l'époque, Grégoire XIII) a remplacé son homologue julien en octobre 1582. Le calendrier julien reposait sur une année fictive comportant 365,25 jours : il comptabilisait le quart de jour excédentaire en imposant une année bissextile de 366 jours tous les 4 ans. Lorsqu'on s'est rendu compte, par un ensemble de mesures astronomiques de la position du soleil, que la vraie valeur tournait plutôt autour de 365,2422 jours, on a été amené à modifier le critère de reconnaissance des années bissextiles selon la règle : les années "multiples de 4 non multiples de 100" ou (inclusif !) les années "multiples de 400". Ce nouveau mode de calcul est meilleur car il table sur une année de 365,2425 jours mais il n'est clairement pas encore parfait (Il faudrait sans doute retirer une année bissextile tous les 4000 ans environ mais à cette échelle temporelle il plane des incertitudes 1) sur la trajectoire terrestre et 2) sur la capacité de l'espèce humaine à se maintenir en vie). Les subtilités relatives au calcul des années bissextiles compliquent l'établissement d'une formule attribuant un jour de la semaine à n'importe quelle date donnée d'avance, sous la forme, d(ay)-m(onth)-y(ear). Ne m'en veuillez pas d'utiliser trois mots anglais mais c'est par respect pour Mike Keith qui a publié la formule réputée la plus simple (Journal of Recreational math. Vol 22 (1980), p 280). Elle s'écrit, j'adapte les notations (accrochez-vous quand même !) :
jour(d,m,y) = Mod[ div(23m,9) + d + 4 + y + div(z,4) - div(z,100) + div(z,400) - If[m≥3,2,0] , 7]
où on a posé : z = If[m≥3,y,y-1].
(Notation : div(a,b) est le quotient entier de a par b, Mod[a,b] est le reste entier laissé par ce quotient et If[condition, a, b] vaut a si la condition est remplie et b sinon. Le résultat est un entier compris entre 0 et 6 qui désigne le jour cherché en commençant par 0 pour dimanche).
Sauf à la programmer, personne n'utilisera jamais cette formule bien trop compliquée. Si vous tenez néanmoins à connaître le jour de votre prochain anniversaire ou de tout autre événement qui vous tient à coeur, Conway a pensé à vous en simplifiant considérablement la procédure. Vous devez simplement connaître le "jour pivot" de l'année qui vous intéresse. Toute année possède son jour pivot; par exemple, en 2020, c'est un samedi. La méthode de Conway vous assure que les jours suivants tombe toujours le jour pivot de l'année en cours :
- Les 4/4, 6/6, 8/8, 10/10 et 12/12 (En effet, à partir de mars, les couples de mois consécutifs comportent 61 jours et 61+2=63 est multiple de 7).
- Le dernier jour de février peu importe qu'il comporte 28 ou 29 jours, ainsi que les jours de mars multiples de 7 (donc les 7/3, 14/3, 21/3 et 28/3 car le dernier jour de février pourrait aussi bien s'appeler le 0 mars).
- Le 3 janvier si l'année est ordinaire (365 jours) et le 4 janvier si elle est bissextile (Retenez 3 et 4, c'est facile).
- Enfin pour les mois restants, débrouillez-vous pour retenir : les 5/9 et 9/5, d'une part, et les 7/11 et 11/7, d'autre part (Observez, par exemple, que 11-7 = 9-5 = 4).
Connaissant le jour pivot vous êtes assez grand pour trouver le jour qui vous intéresse. Par exemple, si l'anniversaire de votre conjoint tombe un 8 octobre, sachant qu'en 2020, le 10/10 est un samedi (le pivot), la réponse est un jeudi.
Encore faut-il connaître le jour pivot pour l'année considérée : il progresse en général d'un jour par année (en 2021, ce sera un dimanche et en 2022 un lundi car 365 est multiple de 7 plus 1) mais attention aux années bissextiles car on saute un jour supplémentaire vu que 366 est multiple de 7 plus 2 ! En cas de doute, voici la formule exacte :
jour_pivot(y) = Mod[2+y+div(y,4)-div(y,100)+div(y,400), 7]
Exemple : jour_pivot(2020) = Mod[2+2020+505-20+5, 7]=Mod[2512,7]=6 → samedi
Vous le constatez, aussi brillant qu'il ait été dans des domaines qui échappent au commun des mortels, Conway a pensé à vous dans de menus problèmes de la vie de tous les jours. Ne manquez pas, en retour, de penser à lui, là où il repose à présent.
Le principe de la descente finie
Le principe de la descente finie résout avec élégance certains problèmes d'abord délicat. On l'applique au décroisement d'un graphe géométrique conçu comme suit :
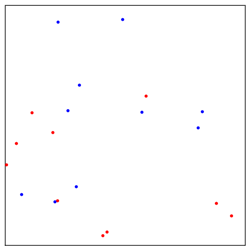
2n points sont disposés au hasard dans une portion de plan (Un carré de côté unité pour fixer les idées sans que cela restreigne en quoi que ce soit). n points sont rouges et n points sont bleus. Etant disposés au hasard, la probabilité que deux points coïncident ou que trois soient collinéaires est nulle donc nous admettons que cette éventualité ne se produit jamais. La figure ci-contre représente un choix possible pour n=10 points de chaque couleur. On relie ensuite au hasard chaque point rouge à un point bleu différent au moyen d'un segment rectiligne (Cf figure suivante). On note la présence possible d'intersections (éventuellement multiples) entre divers segments. Les points ayant été choisis au hasard, trois segments ne sont jamais concourants.
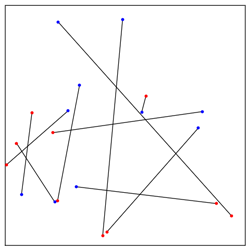
Le graphe ci-dessus illustre une possibilité parmi les n! = 10! = 3 628 800 existantes. Les deux questions posées sont alors les suivantes :
- Démontrer que, quel que soit n, il existe au moins un appariement libre de toute intersection.
- Trouver une procédure algorithmique capable d'en produire un au départ d'un graphe quelconque présentant au moins une intersection (sans considérer tous les cas possibles individuellement).
Les calculs détaillés relatifs à ce problème sont traités en annexe (Notebook Mathematica).
Existence d'au moins un appariement libre d'intersection
On part d'un appariement quelconque et on regarde s'il présente une intersection au moins. Si ce n'est pas le cas, le proposition est vérifiée. S'il c'est le cas, on s'intéresse à la somme des longueurs des segments représentés (L = 5.31546 dans l'exemple traité). Imaginons que nous faisions la même chose en pensée avec les n! appariements possibles. Même sans faire réellement cette opération fastidieuse, nous pouvons être certain qu'elle mène à une liste de n ! valeurs distinctes de L et que dans cette liste se trouve fatalement une valeur de L plus petite que toutes les autres. On énonce que le graphe correspondant à ce Lmin est exempt d'intersection.
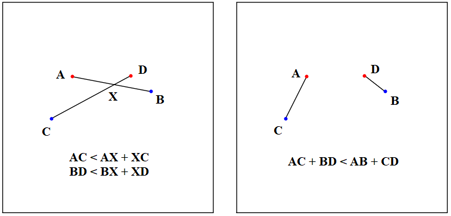
Le principe de la démonstration est simple mais astucieux : les cas intéressants sont ceux où une intersection est présente. On la fait disparaître en permutant les points bleus concernés. Il est certain que lorsque deux segments sont ainsi décroisés, la longueur totale du couple diminue, c'est une conséquence des inégalités triangulaires (dans un triangle un côté est toujours plus court que la somme des deux autres côtés). Autrement dit, en partant d'une figure où les croisements sont éventuellement nombreux et en décroisant systématiquement les couples qui se coupent, on fait diminuer L. Il arrivera inévitablement que soit il n'y aura plus d'intersection à décroiser (auquel cas on aura répondu à la question) soit L (qui ne cesse de diminuer) atteindra sa valeur minimum, Lmin, et plus aucun croisement ne sera présent (sinon il suffirait de le décroiser pour diminuer L en-dessous de sa valeur minimum, ce qui est impossible).
Cette démonstration par descente finie (de L) prouve que le graphe correspondant à Lmin est nécessairement libre d'intersection mais elle n'exclut pas que d'autres appariements, qu'un inventaire systématique révélerait, répondent à la question avec des valeurs de L supérieures à Lmin. Les 8 figures suivantes montrent une suite de décroisements successifs au départ de la figure primitive (n=10) :
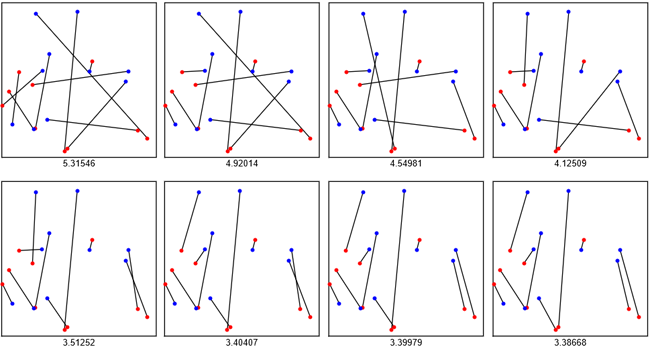
D'autres suites de décroisements menant éventuellement à une solution différente s'obtiennent en partant d'un appariement initial différent, obtenu en permutant les points bleus choisis au départ. Il est évidemment exclu de considérer les 10! cas existants mais on peut tenter d'en chercher l'un ou l'autre en procédant empiriquement au départ de la grille initiale.
En voici une qui part du graphe reliant (rouge)1 à (bleu)3 (au lieu de 1 à 1), 2 à 10 (au lieu de 2 à 2 etc pour la suite), 3 à 5, 4 à 6, 5 à 9, 6 à 7, 7 à 2, 8 à 4, 9 à 1 et 10 à 8 (C'est la permutation de la suite {1, 2, 3, ..., 10} soit {3, 10, 5, 6, 9, 7, 2, 4, 1, 8}, n° 1066281 dans l'ordre adopté par Mathematica). Elle aboutit à une nouvelle solution au terme de trois décroisements (L = 3.08754, valeur sans doute proche de Lmin) :
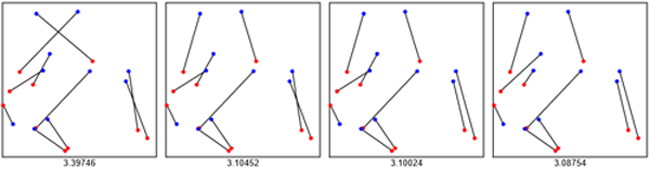
Ce problème n'est pas nouveau et il est réapparu récemment dans les chroniques Quora animées avec compétence et talent par Alon Amit. Le titre adopté fait écho au principe de la descente infinie de Fermat éventuellement invoquée pour démontrer qu'une proposition, P(n), dépendant de l'entier naturel n, est fausse pour tout n. Note. La formulation traditionnelle de la méthode de Fermat repose sur une récurrence infinie montrant que si P(n) était vraie, il existerait un m (<n) tel que P(m) le serait également, ce qui est impossible puisque m doit rester positif. Cet argument, faisant intervenir des nombres sortant du cadre prédéfini des entiers positifs, peut paraître suspect d'où on lui préfère actuellement une variante proche de la descente finie décrite ci-avant (Cf l'article Wikipedia consacré à la descente de Fermat).
Annexe : Critère d'intersection et Procédure effective
Les figures précédentes ont été construites avec l'aide d'un programme (Mathematica) qui fonctionne simplement comme suit :
- Les coordonnées des points de départ sont reprises dans deux listes notées, rouge = {{xr1, yr1}, {xr2, yr2}, ...} et bleu = {{xb1, yb1}, {xb2, yb2}, ...}. La liste "rouge" est immuable, par contre la liste "bleu" peut exister dans l'une quelconque des n! permutations possibles.
- Quelle que soit la permutation retenue, les segments sont tirés entre les points rouges et bleus de même indice. Dans le programme on n'a considéré que deux cas correspondant aux permutations n°1 et 1066281.
S'il est facile d'écrire les équations des droites passant par deux points et de calculer leur intersection, il est moins évident de déterminer le critère qui situe cette intersection à l'intérieur des segments concernés. Trois cas seulement sont possibles dont on ne retient que le troisième pour des raisons qui apparaissent clairement sur les figures suivantes :
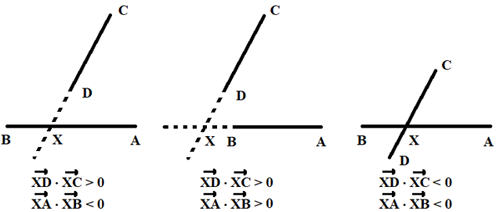
Les calculs ne sont pas immédiats mais les résultats s'expriment aisément en termes de produits de deux déterminants :
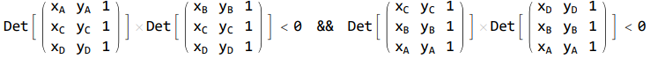
Triangles à côtés entiers dont deux angles sont en rapport entier
Le problème suivant est réapparu sur le réseau Quora où il a reçu l'attention d'Alon Amit, un mathématicien dont les interventions sont toujours pertinentes. Il a abordé quelques cas particuliers dans sa réponse, qu'il a traités par une approche purement géométrique. L'approche trigonométrique qui suit semble plus commode si on envisage le cas général.
Trouver un triangle dont les trois côtés, a, b et c, sont de longueur entière est banal. De fait, tous les triplets {a, b, c} sont possibles du moment que les inégalités triangulaires sont respectées, à savoir : tout côté doit être inférieur à la somme des deux autres. Ces trois conditions peuvent être condensées en une seule à condition de partir du côté le plus grand. On rend le problème plus intéressant en imposant une condition supplémentaire portant sur les angles.
Voici l'énoncé complet : Trouver les triangles ABC dont tous les côtés, a, b et c, sont entiers avec la condition supplémentaire que l'angle en B soit k fois plus grand que celui en A, k étant un entier positif.
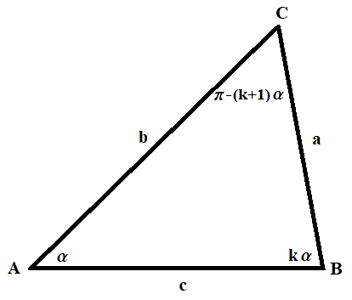
D'après les conditions du problème, les angles en A, B et C valent, dans l'ordre, α, k α et (fatalement) π - (k+1)α. Aucun angle ne pouvant être négatif ni supérieur à π (radians), on a la double condition évidente : 0 < α < π/(k+1).
La relation des sinus dans ABC, s'écrit comme suit :
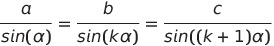
Pour que les côtés du triangle soient de longueurs entières, il faut à tout le moins que les quotients, sin(k α)/sin(α) et sin((k+1) α)/sin(α) soient rationnels. A ce stade, la famille des polynômes de Tchebychev de deuxième espèce, U(k,z), volent à notre secours du fait de l'identité remarquable qui les caractérise : sin(α) U(k, cos(α)) = sin((k+1)α). Les U(k,z) sont des polynômes de degré k et ils forment une famille dont les premiers membres sont : U(0, cos(α)) = 1, U(1, cos(α)) = 2 cos(α), U(2, cos(α)) = 4 cos2(α) -1, U(3, cos(α)) = 8 cos3(α) - 4 cos(α), etc (Les calculs détaillés relatifs à ce problème sont détaillés en annexe (Notebook Mathematica)).
La relation entre les côtés se note à présent :
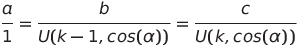
Les côtés des triangles cherchés obéissent donc à la relation de proportionnalité, {a, b, c} ∝ {1, U(k-1, cos(α)), U(k, cos(α)). Pour qu'ils soient de longueurs entières, il faut que les polynômes, U, de degrés, k-1 et k, calculés en cos(α), soient rationnels. Pour qu'il en soit ainsi, il faut que cos(α) soit lui-même rationnel, soit cos (α) = m/(2n) où m et n sont entiers positifs (Le facteur 2 n'est pas indispensable mais l'omettre autoriserait des solutions redondantes).
La relation précédente se note à présent : {a, b, c} ∝ {1, U(k-1, m/(2n)), U(k, m/(2n)), soit pour les 5 premières valeurs de k = 1, 2, 3, 4, 5 : {a, b, c} ∝

On rend les solutions, a, b et c, définitivement entières en multipliant les valeurs trouvées par nk, ce qui livre la solution finale : {a, b, c} =
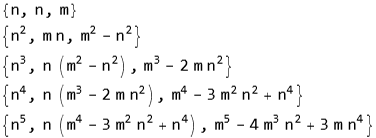
Reste à trouver les valeurs autorisées pour les entiers m et n. Elles dérivent comme suit des conditions déjà mentionnées, 0 < α < π/(k+1) et 0 < cos(α) < 1. α est manifestement inférieur à π/2; or cos(α) décroît monotonément entre 0 et π/2 donc la condition 0 < α < π/(k+1) devient : cos(π/(k+1)) < cos(α) < 1 ou encore, en inversant, 1/cos(π/(k+1)) > 1/cos(α) > 1. Remplaçant cos (α) par m/(2n), on trouve finalement la condition limitant les valeurs des entiers m et n :
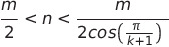
On a dès lors la procédure suivante qui énumère les solutions au problème posé : pour tout k entier positif, on considère successivement les valeurs de m entières et positives et on regarde pour quelles valeurs de n la condition précédente est satisfaite.
Par exemple, pour k=2, la condition s'écrit m/2 < n < m, jamais satisfaite si m = 1 ou 2 mais satisfaite si m = 3 (et n = 2, livrant le triangle {4, 6, 5}), satisfaite également si m = 4 (et n = 3, livrant le triangle {9, 12, 17}), satisfaite également si m = 5 (et n = 3 ou 4, livrant les triangles {9, 15, 16} et {16, 20, 9}), etc.
Autre exemple, pour k=3, la condition devient m/2 < n < m/√2, jamais satisfaite si m = 1, 2 ou 4 mais satisfaite si m = 3 (et n = 2, livrant le triangle {8, 10, 3}), satisfaite également si m = 5 (et n = 3, livrant le triangle {27, 48, 35}), satisfaite également si m = 6 (et n = 4, livrant le triangle {64, 80, 24}), etc.
Voci les douze premiers triangles trouvés dans les cas k = 2, 3 et 4 (Le cas k = 1 est peu intéressant car il ne construit que des triangles isocèles; les cas suivants sont détaillés dans le Notebook Mathematica déjà mentionné. Le programme permet également de vérifier que l'angle en B vaut k fois l'angle en A).
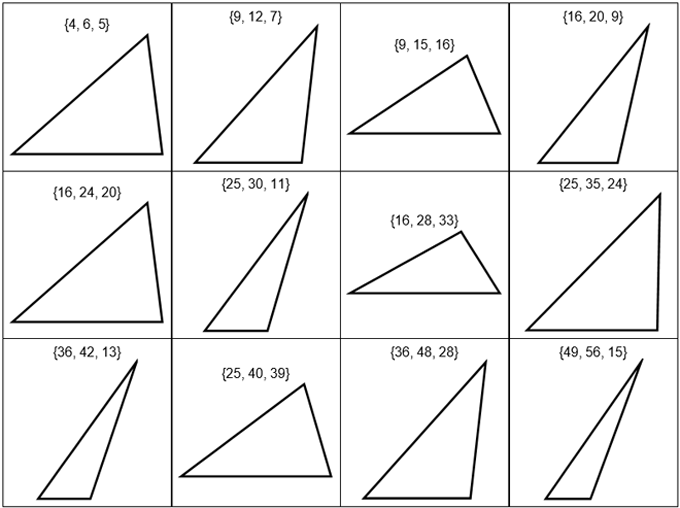
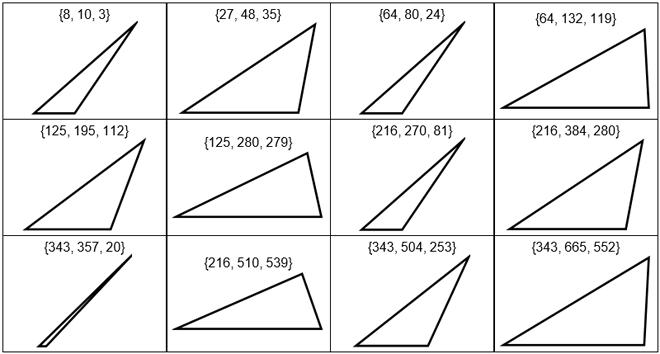
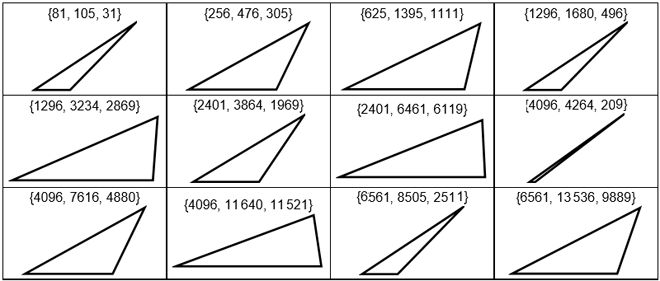
Les valeurs suivantes de k se traitent de la même façon : elles présentent toutes une infinité de solutions impliquant des côtés entiers de plus en plus longs et espacés. Dans tous les cas, le côté, a, opposé au sommet A vaut toujours la puissance k d'un entier, précisément a = nk.
Un puzzle pythagoricien
Le théorème de Pythagore est un grand classique de la géométrie euclidienne. Il en existe des dizaines de démonstrations plus ou moins simples et/ou astucieuses, telles celles (au nombre de 118 !) répertoriées sur ce site. Certaines sont ludiques en ce qu'elles reposent sur l'examen de puzzles accessibles à tous âges (quelques pièces à peine !) mais qui peuvent dérouter si l'on ne s'y prend pas bien. Les paragraphes qui suivent s'inspirent de la démonstration n°14, attribuée à Henry Perigal (1872) et redécouverte ultérieurement par Henry Dudeney.
Rappelons que le théorème de Pythagore s'énonce simplement : dans tout triangle rectangle ABC, de côtés a, b et c et d'angles opposés, α, β (= π/2 - α) et π/2, l'aire du carré construit sur l'hypoténuse, c, vaut la somme des aires des carrés construits sur les deux côtés de l'angle droit, a et b, soit : a2 + b2 = c2.
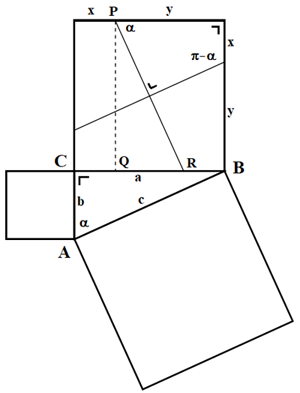
La figure ci-contre reproduit les données du problème et la construction de Perigal. La triangle rectangle de départ est noté ABC tel que a ≥ b. Par le centre du carré construit sur la base du côté noté a, on mène les parallèles aux côtés du carré construit sur l'hypoténuse. On partitionne ainsi le carré construit sur a en quatre quadrilatères égaux régulièrement réorientés. Ils forment les quatre pièces d'un puzzle élémentaire.
Si, à partir de P, on abaisse la perpendiculaire sur CB, on délimite un triangle, PQR, égal au triangle de départ : PQR = ABC (Les angles à côtés perpendiculaires sont égaux et le côté a est commun). On en déduit que QR = b et PR = c, ce qui suffit pour calculer les longueurs des côtés de chaque pièce du puzzle.
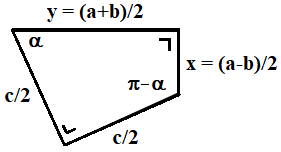
Vu la symétrie de la figure initiale, on a simultanément : x + y = a et 2x + b = a, d'où ont tire les longueurs des côtés de l'angle droit : x = (a-b)/2 et y = (a+b)/2. De plus, les deux côtés restants sont égaux à c/2. Tout cela est résumé dans la figure ci-contre.
On procède ensuite à la manoeuvre de Perigal, qui consiste, 1) à faire tourner chaque quadrilatère d'un angle 3π/2 - α = π + arctg(b/a), dans le sens des aiguilles d'une montre, autour du sommet du carré qui lui appartient et, 2) à opérer les translations nécessaires pour assembler les 4 pièces (Pour l'automatisation des calculs, cf annexe ou le Notebook Mathematica). La figure dynamique suivante illustre ces opérations (Actionnez le curseur situé en bas de l'écran) :
On voit que les pièces du puzzle sont réarrangées de telle manière qu'un grand carré (rouge) est constitué présentant un carré vacant en son milieu. Il se fait que le carré rouge est égal au carré construit sur l'hypoténuse tandis que le petit carré vacant coïncide avec le carré construit sur le côté b, ce que l'on aurait pu montrer en poursuivant l'animation et en déplaçant les pièces. Ce n'est toutefois pas nécessaire ni souhaitable car montrer n'est pas démontrer et il convient à ce stade de s'assurer que la relation de Pythagore est bien démontrée :
- Le grand carré résultant (rouge) est bien constitué car ses côtés sont rectilignes (Les angles constitutifs sont supplémentaires). De plus, ils sont tous égaux à c/2 + c/2 = c.
- Le carré central est également bien constitué car ses angles sont droits et ses côtés égaux à : (a+b)/2 - (a-b)/2 = b.
- L'aire du grand carré rouge, de côté c, vaut manifestement la somme des aires des quadrilatères constituant le carré initial (de côté a) et de l'aire du carré central (de côté b), soit : a2 + b2 = c2 (CQFD).
Vous pouvez amuser vos enfants pendant une longue soirée d'hiver en leur faisant découper dans un carton de couleur (afin de ne pas mélanger le recto et le verso !) deux carrés de côtés a et b de bonnes dimensions (Pour des raisons esthétiques, un rapport a/b de l'ordre de 2.2 fait parfaitement l'affaire) puis en découpant à nouveau le grand carré en 4 quadrilatères égaux selon la manoeuvre décrite (Le plus simple est de reporter le segment x = (a-b)/2 à partir de chaque sommet et de joindre les points opposés tels P et R dans la figure initiale). Deux puzzles sont alors possibles, demandant de constituer deux carrés parfaits : le premier, facile, n'utilisant que les 4 quadrilatères et le second, plus difficile, exigeant d'inclure le petit carré comme cinquième pièce. Si tout se passe comme prévu vous devriez avoir la paix pendant une heure au moins.
Un problème de trigonométrie "diophantienne"
Le problème suivant est élémentaire : dans le carré ABCD, de côté unitaire, c = 1, les points X et Y sont situés respectivement sur les segments CD et BC (extrémités exclues) de telle façon que les angles BAY et YAX valent respectivement u = 20° et v = 45°. On demande de calculer l'angle w = YXA.
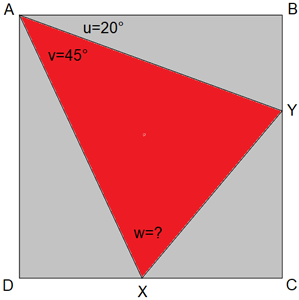
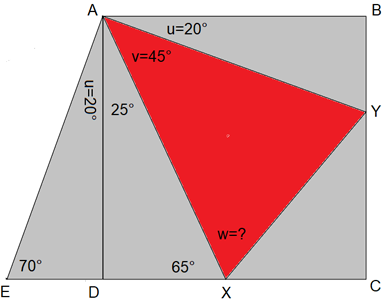
Ce problème reçoit une solution immédiate si on a la bonne idée de compléter la figure de départ par adjonction d'une copie (ADE) du triangle ABY, tournée de 90° dans le sens horlogique.
Il devrait être évident pour le lecteur que les triangles AYX et AXE sont égaux (AE = AY, AX est commun et les angles XAY et EAX sont égaux à 45°. On en déduit que les angles EXA et AXY sont également égaux, soit w = EXA = 65°.
Il peut paraître surprenant, à ce stade, que u et v, possédant des valeurs entières en degrés, il en aille de même de w. Pourtant, cela n'a a priori rien d'invraisemblable car, après tout, lorsqu'on se donne deux angles "entiers en degrés" d'un triangle, on a la certitude que le troisième l'est également puisque leur somme doit valoir 180°. Cependant le cas est différent ici car il n'existe a priori aucune relation simple entre u, v et w.
On s'en rend compte en résolvant complètement la figure dans le cas général où u et v sont quelconques. On y parvient en appliquant la relation des sinus au triangle AYX. On a successivement :
c/AX = cos[90°-(u+v)], c/AY = cos(u), d'où on tire : AY/AX = sin(u+v)/cos(u).
Mais on a aussi (relation des sinus dans AYX) : sin(w)/AY = sin[180°-(v+w)]/AX.
Comparant les valeurs trouvées pour AY/AX, on obtient, après réduction, la relation qui relie les angles u, v et w , dans le cas général : sin(u+v) sin(v+w) = sin(w) cos(u). Vu qu'on cherche w, cette relation peut se réécrire sous la forme définitive :
tg(w) = sin(v) sin(u+v) / [cos(u) - cos(v) sin(u+v)]
Si u = 20° et v = 45°, comme imposé dans le problème initial, on trouve bien, après inversion de la tangente : w = 65°.
Note. Ce calcul numérique est normalement confié à un logiciel, dans notre cas Mathematica, et il y a un piège qu'il convient d'éviter lorsque la valeur de tg(w) est négative, ce qui se produit effectivement pour certaines valeurs de u et v. La fonction inverse, arctg, est, en fait, multivaluée à un multiple entier de π et les logiciels numériques n'affichent que sa valeur principale, conventionnellement confinée dans l'intervalle, ]-π/2, +π/2[. Avec cette convention, toute valeur négative de tg(w) livre une valeur négative pour w ce qui n'a aucun sens dans le cas qui nous occupe. Lorsque ce cas se produit, il y a donc lieu d'ajouter π = 180° au résultat trouvé pour la tangente inverse. Cela est rappelé en tête du fichier Mathematica joint.
Voyons à présent ce qui se passe si l'on part de valeurs entières quelconques pour les angles u et v, tout en restant dans les limites imposées par la géométrie de la figure initiale soit, 0 < u< 45° et 45°-u <v <91°-u. 1980 choix d'angles existent dans ce cas, qu'il est facile de lister (Cf le fichier Mathematica). On observe, comme attendu, que w cesse souvent d'être à valeur entière en degré, la fonction arctg(w) menant la plupart du temps à des valeurs irrationnelles. La surprise vient de ce que dans 88 cas sur 1980, w redevient entier en respectant une régularité parfaite : pour tout u allant de 1° à 44°, il existe deux possibilités, v = 45° et v = 90° - 2u et dans les deux cas, w = 45°+u.

La figure dynamique suivante illustre ces 88 possibilités (Balayez lentement à l'aide du curseur situé en bas du cadre) : l'angle u est marqué en rouge, les deux angles v possibles sont marqués en bleu et l'angle w est marqué en vert.
La régularité observée traduit évidemment une propriété d'annulation de la fonction, tg(45°+u) [cos(u) - cos(v) sin(u+v)] - sin(v) sin(u+v). On a en effet que lorsqu'on pose w = 45°+u, celle-ci se factorise en cos(2u+v) (cos(v)-sin(v))/(cos(u)-sin(u)), qui s'annule dans deux cas : 1) si cos(v) = sin (v) soit v = 45° ou 2) si cos(2u+v) = 0 soit v = 90° - 2u. Dans tous les autres cas, l'inventaire numérique, fini donc complet, permet d'affirmer que cette fonction ne s'annule jamais pour des valeurs simultanément entières de u et de v. Les solutions au problème "diophantien" posé sont donc celles reprises au tableau précédent (ou dans l'application dynamique).
Pour l'automatisation des calculs, cf annexe ou le Notebook Mathematica.
Le Problème 6 des Olympiades 1988
Le problème suivant a été posé lors des Olympiades de mathématiques qui se sont déroulées en Australie en 1988 (IMO 1988). Soumis par un mathématicien d'Allemagne de l'Est, il a failli être refusé au motif qu'un jury d'experts n'est pas parvenu à le résoudre au terme du délai raisonnable imposé. Après délibération, il a cependant été incorporé à la liste des 6 problèmes de l'année 1988, avec la mention "difficile".
Une solution devait pourtant exister car on imagine mal que celui qui a proposé le problème se serait contenté d'une simple conjecture susceptible de s'avérer fausse. Dans les faits, 11 candidats sur les 300 participants ont résolu le problème dont, pour la petite histoire, l'actuel président de la république roumaine, Nicușor Dan (19 ans à l'époque).
Enoncé : a et b étant deux entiers positifs, si a b +1 divise a2 + b2, alors le quotient, q = (a2 + b2) / (a b + 1) est un carré parfait (q = k2, k entier).
Il est d'usage d'ignorer les cas triviaux où, 1) a (ou b) serait nul et 2) a serait égal à b (qui aurait pour seule solution : a = b = 1). De plus, vu que a et b sont interchangeables, on ne s'intéresse qu'aux cas où a < b (ou a>b, le choix est indifférent).
Les jeunes candidats qui ont résolu ce problème ont fait preuve d'inventivité en combinant trois méthodes, la bascule de Viète, la descente de Fermat et le raisonnement par l'absurde.
Les solutions proposées ont depuis fait l'objet de réexamens et on dispose aujourd'hui de solutions simples dont une particulièrement courte, claire et nette sous la plume de Kevin S. Brown (Mathpages). Elle est tellement concise qu'elle risque de passer pour hermétique auprès de nombre de lecteurs. L'aide numérique proposée ci-après aide à la compréhension du point délicat, la bascule de Viète, et la démonstration complète suit. On trouvera les calculs menant à l'inventaire complet des solutions dans l'annexe ou le Notebook Mathematica et, en prime, la solution générale condensée en une formule unique (ce que le problème initial ne demandait pas).
La variante où le dénominateur (a b + 1) est remplacée par (a b - 1) est également étudiée en deuxième partie.
Le principe de la démonstration
L'équation de départ est : (a2 + b2) / (a b + 1) = q, où q est un entier, sans autre précision à ce stade. Si on chasse le dénominateur, on voit que, b et q étant fixés, a est solution de l'équation quadratique : a2 - (q b) a + (b2 - q) = 0. Celle-ci possède deux racines, a1 et a2, entre lesquelles existent deux relations remarquables (formules de Viète), a1 + a2 = q b et a1 a2 = b2 - q. On en déduit que "si le couple (a1, b1) est un cas de divisibilité, il en va de même du couple (a2 = q b1 - a1, b1) et le quotient est le même (q)". On peut vérifier que a2 < a1 et b2 < b1, conséquences des relations de Viète. Pour poursuivre le raisonnement, la manoeuvre suivante s'avère cruciale : il convient d'inverser l'ordre dans le couple (a, b) généré, ce qui est licite puisque a et b sont en position de symétrie à toutes les étapes du raisonnement. La proposition précédente devient alors : "si le couple (a1, b1) représente un cas de divisibilité, il en va de même du couple (a2 = b1, b2 = q b1 - a1) et le quotient reste le même (q)".
Voyons cela sur l'exemple du couple, (a1 = 112, b1= 30). C'est un cas de divisibilité et le quotient vaut, q = 4. Le couple (a2 = q b1 - a1, b1) = (8, 30) est une nouvelle solution que l'on réécrit sous la forme inversée (a2 = b1, b2 = q b1 - a1) soit (30, 8).
On peut alors recommencer la manoeuvre et ainsi trouver les couples-solutions successifs (ai, bi) formant une suite strictement décroissantes et partageant le même quotient (ici, 4 = 22) :
a1 = 112 et b1 = 30, on vérifie que (1122 + 302)/(112 x 30 + 1) = 4
a2 = 30 et b2 = 8, on vérifie que (302 + 82)/(30 x 8 +1) = 4
a3 = 8 et b3 = 2, on vérifie que (82 + 22)/(8 x 2 +1) = 4
a4 = 2 et b3 = 0, on vérifie que (22 + 02)/(2 x 0 +1) = 4
a5 = 0 et on s'arrête là.
Un exemple n'a évidemment pas valeur de démonstration mais il permet de formaliser le cas général où l'on part d'une solution quelconque, (a1, b1), telle que le quotient, q, soit un entier positif. Paraphrasant l'exemple, on construit la suite strictement décroissante de couples (ai, bi), qui constituent autant de solutions partageant la même valeur de q. Ces couples obéissent au système récurrent couplé, ai+1 = bi et bi+1 = q bi - ai, où i = 1, 2, 3, ... ..
On arrête l'itération lorsque b atteint la valeur 0, ce qui ne peut manquer de se produire car si ce n'était pas le cas, cela signifierait qu'on aurait trouvé pour le couple bi et bi+1 (donc ai+1 et bi+1), deux valeurs de signes contraires. (ai+12 + bi+12) / (ai+1 bi+1 + 1) serait alors négatif (ou infini si le produit ai+1 bi+1 = -1), ce qui est impossible puisque q, ne change jamais de valeur (finie et positive) lors de la descente récurrente.
Lorsque b vaut 0, il ne subsiste de l'équation de départ que a2 = q, ce qui prouve que q est effectivement un carré parfait dans ce cas (q = k2).
Cette méthode descendante génère un nombre fini de solutions au départ d'une solution que l'on aurait trouvée préalablement par un procédé numérique quelconque mais ce que l'on veut c'est trouver toutes les solutions sans en invoquer une seule a priori.
On y parvient, 1) en découplant le système récurrent sous la forme, ai+1 = q ai - ai-1 (idem bi+1 = q bi - bi-1 puisque les bi prennent les mêmes valeurs que les ai avec un temps d'avance (ai+1 = bi)) et, 2) en lançant cette récurrence, en sens ascendant, au départ des conditions initiales, a0 = 0 et a1 = k (où k = 2, 3, ..., au choix).
Par exemple, aux petites valeurs de k (donc de q = k2), on trouve pour les couples-solutions (ai, bi) les familles suivantes :
- si k = 2 donc q = 22 = 4 : (0, 2), (2, 8), (8, 30), (30, 112), etc ...
- si k = 3 donc q = 32 = 9 : (0, 3), (3, 27), (27, 240), (240, 2133), etc ...
- si k = 4 donc q = 42 = 16 : (0, 4), (4, 64), (64, 1020), (1020, 16256), etc ...
etc ...
Il est possible de condenser ces solutions car la récurrence, ai+1 = q ai - ai-1 (avec a0 = 0 et a1 = k) est soluble exactement en termes de polynômes de Tchebychev de deuxième espèce, Ui(z). On trouve précisément :
(ai , bi) = (q Ui(k2/2), q Ui+1(k2/2))
Au bilan, l'identité remarquable suivante résume l'ensemble des solutions au problème posé (i = 0, 1, 2, ..., k = 2, 3, 4, ... et q = k2 ) :
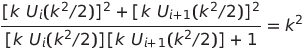
Cette identité demeure vraie lorsque k cesse d'être entier et devient réel ou même complexe.
Une variante
Il suffit de modifier légèrement l'énoncé de départ pour que l'ensemble des solutions change radicalement.
Enoncé : a et b étant deux entiers positifs, si a b - 1 divise a2 + b2, alors le quotient, q = (a2 + b2) / (a b - 1), ne peut prendre que la seule valeur, q = 5, donnant naissance à deux familles de solutions pour le couple (a, b).
Cet énoncé est étroitement relié au précédent, où la condition que les variables a et b soient de même signe a simplement été remplacée par celle où elles sont de signe contraire. K. S. Brown évoque cette variante dans l'article déjà mentionné mais il ne fournit ni démonstration ni surtout de formule condensant l'ensemble des solutions.
La démonstration commence comme précédemment en partant d'un cas quelconque de divisibilité de (a2 + b2) par (a b - 1) où le quotient, q, est un entier sans autre précision à ce stade.
On peut reproduire fidèlement le raisonnement précédent, jusqu'à la conclusion "si le couple (a1, b1) représente un cas de divisibilité, il en va de même du couple (a2 = b1, b2 = q b1 - a1) et le quotient reste le même (q)".
Voyons cela sur l'exemple du couple, a1 = 206 et b1= 43. C'est un cas de divisibilité et il se trouve que le quotient vaut q = 5. On a successivement :
a1 = 206 et b1 = 43, on vérifie que (2062 + 432)/(206 x 43 - 1) =5
a2 = 43 et b2 = 9, on vérifie que (432 + 92)/(43 x 9 - 1) = 5
a3 = 9 et b3 = 2, on vérifie que (92 + 22)/(9 x 2 - 1) = 5
a4 = 2 et b3 = 1, on vérifie que (22 + 12)/(2 x 1 - 1) = 5
a5 = 1 et on s'arrête là.
On a trouvé, pour les bi, la suite récurrente strictement décroissante, 43, 9, 2, 1 et on s'est arrêté là car lorsque b vaut 1, il ne reste de l'équation de départ que (a2 + 1) = (a - 1) q, qui, on va le démontrer, impose que le quotient soit égal à : q = 5.
Avant de poursuivre, il faut la preuve que la suite descendante des bi passe obligatoirement par la valeur, 1, dans tous les cas de divisibilité. Or cela est certain car si ce n'était pas le cas, on finirait par trouver un couple bi et bi+1 (donc ai+1 et bi+1) dont les valeurs entières seraient situées de part et d'autre de la valeur 1 et telles que (a2 + b2) / (a b - 1) serait négatif (ou infini si le produit a b = -1), ce qui est impossible puisque q ne change jamais de valeur (positive) lors de la descente récurrente.
Pour démontrer que l'équation quadratique en a, (a2 + 1) = (a - 1) q entraîne q = 5, on considère ses deux solutions, a = (q ± (q2 - 4q - 4)1/2)/2. a étant entier, le discriminant doit être un carré parfait, soit : q2 - 4q - 4 = n2, d'où q = 2 ± (n2 + 8)1/2. q doit aussi être entier, ce qui ne se produit que si n = 1 (si n>1, n'ajouter que 8 à n2 ne peut donner un autre carré parfait). Si n vaut 1, q vaut 5 et l'équation en a se simplifie en a2 - 5 a + 6 = 0, dont les seules racines sont a = 2 et a = 3. Lors de la descente récurrente, a (donc aussi b) doit donc finir passer par 2 (ou 3) puis par 1.
Développant la récurrence, ai+1 = 5 ai - ai-1, en sens inverse (donc ascendant), au départ des conditions initiales, a0 = 1 et a1 = 2 (ou 3), on génère deux familles de couples (ai, bi) solutions de l'équation modifiée et on peut même proposer une formule générale qui les résume toutes, impliquant à nouveau des polynômes de Tchebychev :
- (1, 2), (2, 9), (9, 43), (43, 206), etc ... , soit : (ai , bi) = (Ui(5/2) - 3 Ui-1(5/2), Ui+1(5/2) - 3 Ui(5/2))
- (1, 3), (3,14), (14, 67), (67, 321), etc ..., soit : (ai , bi) = (Ui(5/2) - 2 Ui-1(5/2), Ui+1(5/2) - 2 Ui(5/2))
(avec la convention U-1(z) = 0). Dans les deux cas, q = 5.