Info
Quelques problèmes informatiques curieux ou amusants
Sommaire
[ afficher ]- Le problème des 12, 39, 120, ..., boules
- Quelques exemples de programmes en langage Fractran
- Une variante aisée du tour de Cheney
- Devinez l'entier !
- Fonctions de Walsh et compression avec perte
- Statistique de la production des machines de Turing binaires simples (MTS)
- Compression sémantique des suites binaires courtes par MTS
Cette section, en construction permanente, présente des questions exotiques ou amusantes d'informatique théorique.
Le problème des 12, 39, 120, ..., boules
Ce problème récréatif illustre la notion de bilan informationnel : on donne N boules, d'apparences identiques sauf que l'une d'entre elles est peut-être plus lourde ou plus légère que les autres. Combien de pesées sont nécessaires pour identifier l'intruse éventuelle ? On ne dispose que d'une balance à fléau, non graduée. Classiquement, on ne considère que le cas, N=12 qui se règle en k=3 pesées.
La théorie de l'information apporte une solution élégante au problème général. L'information manquante se calcule sur base du logarithme (en base 2) du nombre des solutions possibles, supposées équiprobables, soit, ℓg(2N+1) bits (Dans le cas, N=12, cela représente ℓg25 = 4.64386 bits).
L'apport informationnel d'une pesée dépend du nombre de boules que l'on dépose dans chaque plateau. Si on dépose x boules de chaque côté, les probabilités que le fléau penche à gauche, reste en équilibre ou penche à droite valent respectivement:
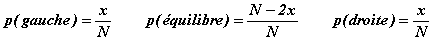
L'apport d'information se calcule sur base de la formule de Claude Shannon :
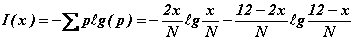
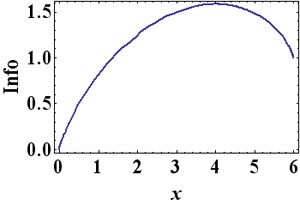
Cette fonction est maximum lorsque x=N/3 (soit x=4 dans l'exemple de 12 boules).
Cette pesée favorable apporte ℓg3 = 1.585 bits par pesée indépendante.
Vu que 3 x 1.585 = 4.75489 > 4.64386 (bits), rien ne semble s'opposer à ce qu'il existe une solution en k=3 pesées dans le cas N=12 (dont l'existence ne peut être établie qu'en la détaillant !).
La solution proposée par John Conway, l'un des mathématiciens les plus inventifs de sa génération, est particulièrement élégante. On détaille l'exemple classique k=3, N=12 mais la généralisation est immédiate, disponible en annexe (Notebook Mathematica).
Quel que soit k, Conway travaille sur un alphabet de 3 lettres, G, D et E, observant qu'il permet de former 3k = 27 mots distincts de k=3 lettres. De cette liste, il enlève les mots constants, GGG, DDD et EEE, ne retenant que ceux où le premier changement de lettre respecte l'un des schémas GD DE ou EG. Au bilan il reste 12 mots distincts qu'il associe à chacune des 12 boules :
GGD GDG GDD GDE DDE DEG DED DEE EGG EGD EGE EEG
Les trois pesées mettent en balance les boules suivantes :
| 1: | GGD GDG GDD GDE | DDE DEG DED DEE |
|---|---|---|
| 2: | GGD EGG EGD EGE | GDG GDD GDE DDE |
| 3: | GDG DEG EGG EEG | GGD GDD DED EGD |
où la iième pesée place les boules codées par G en iième position à gauche et celles codées par D en iième position à droite. Chaque pesée fournit un résultat que l'on note, G, si le fléau penche à gauche, D, s'il penche à droite et, E, s'il reste en équilibre. Les trois lettres, prises dans cet ordre, forment un mot. S'il fait partie de la liste des 12 mots retenus, il désigne la boule anormale et elle est plus lourde. S'il n'en fait pas partie, il suffit de transposer les lettres D et G pour désigner la boule anormale et elle est plus légère. Si le mot trouvé est EEE, toutes les boules sont identiques. GGG et DDD n'apparaissent jamais.
La méthode de Conway se généralise immédiatement à un nombre plus grand de pesées (et de boules !). La pesée la plus porteuse d'information place x = N/3 boules dans chaque plateau (à condition que N soit divisible par 3 !), amenant ℓg3 = 1.585 bits. On serait alors tenté de raisonner ainsi : k pesées indépendantes apportent k ℓg3 (bits) or il faut combler ℓg(2N+1) bits d'information manquante d'où k pesées devraient venir à bout du problème à N=(3k-1)/2 boules. C'est un peu vite dit car ce N-là n'est pas multiple de 3 d'où l'information apportée par chaque mesure est inférieure au maximum escompté, 1.585 bits. En fait, (3k-2)/2 n'est pas davantage multiple de 3, par contre N = (3k-3)/2 l'est. C'est la solution optimale cherchée et la construction de Conway continue de s'appliquer.
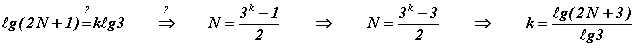
En résumé, k pesées résolvent le problème des (3k-3)/2 boules et inversement. En particulier, 2,3,4,5, …, pesées suffisent tout juste pour régler le problème comportant 3, 12, 39, 120, …, boules.
Quelques exemples de programmes en langage Fractran
John Conway est encore à l'honneur grâce à l'un de ces joyaux dont il a le secret : Fractran. Il a publié l'essentiel de son travail, en 1987, dans l'ouvrage collectif "Open Problems in Communication and Computation (Springer Verlag)". Ce résumé s'inspire de cette publication et de quelques essais isolés, parus dans des forums spécialisés.
Fractran est un langage un brin ésotérique mais universel au sens de Turing donc équivalent au modèle de la machine du même nom, qui incarne classiquement la notion de calcul. On sait que le kit minimal d'instructions nécessaires à la programmtion de n'importe quelle fonction calculable est ridiculement mince. On connait plusieurs modèles calculatoires formellement équivalents dont le plus simple est sans doute la machine à registres présentée par ailleurs sur ce site, à la rubrique Séminaires. Fractran est équivalent à la machine à registres grâce au fait que tout entier naturel possède une décomposition unique en facteurs premiers, les atomes de l'arithmétique. Ainsi l'entier, 600 = 233152 peut être vu comme l'encodage des entiers 3, 1 et 2 dans trois registres distincts. A partir de ces prémices, Conway a imaginé le langage suivant :
- Tout algorithme applique un programme à un ensemble de données. Un programme Fractran est représenté par une suite, F, ordonnée et finie, de fractions rationnelles. Les données sont représentées par un entier, n. L'algorithme fonctionne itérativement comme suit :
- L'entier n est multiplié successivement par les fractions de la suite F jusqu'à tomber sur un entier. Lorsque celui-ci est trouvé, il prend la place de n et le processus des multiplications successives recommence. Le calcul s'interrompt lorsqu'aucun produit n'est trouvé entier : l'entier en cours est alors imprimé. Le lecteur vérifiera, à la main, que les programmes suivants effectuent les tâches algorithmiques annoncées. Il peut aussi se référer aux programmes joints en annexe (Notebook Mathematica). Il notera qu'il est possible de proposer des progammes Fractran concis qui effectuent des tâches non triviales, une performance généralement interdite aux machines de Turing. Les plus curieux chercheront d'autres exemples mais la recherche des programmes, F, requiert une certaine expertise.
Six programmes simples
- Addition de deux entiers
Ce programme, sans doute le plus simple de tous, ne comporte qu'une seule instruction, F = {3/2}. Les entiers à additionner, x et y, sont encodés sous la forme, n = 2x3y. Les multiplications successives déroulent le programme comme suit, jusqu'à l'arrêt où le résultat s'affiche en exposant de 3 :
2x3y → 2x-13y+1 → 2x-23y+2 → ... → 3x+y
On remarque que le même programme permet de transférer le contenu d'un registre vers un autre registre : 2x → ... -> 3x. Quant au programme, F = {3a/2}, il calcule la fonction, y+ax selon le schéma : 2x3y → 3y+ax. - Multiplication de deux entiers
Ce programme légèrement plus long, requiert 6 instructions, F = {455/33, 11/13, 1/11, 3/7, 11/2, 1/3}. Les entiers à multiplier, x et y, sont encodés sous la forme, n = 2x3y et le résultat s'affiche, au moment de l'arrêt, sous la forme d'une puissance de 5 :
2x3y → ... → 5xy - Division entière
Ce programme utilise 8 instructions, F = {91/66, 11/13, 1/33, 85/11, 57/119, 17/19, 11/17, 1/3}. Les entiers à diviser, x et y, sont encodés sous la forme, n = 2x3y11. Au terme du calcul, le quotient (entier) s'affiche en exposant de 5 et le reste (entier) s'affiche en exposant de 7 :
2x3y11 → ... → 5Integer[x/y] 7Mod[x,y] - PGCD
Ce programme utilise 11 instructions, F = {22/19, 21/23, 51/55, 11/17, 26/35, 7/13, 1/11, 1/7, 5/6, 23/3, 19/2}. Les entiers donnés, x et y, sont encodés sous la forme, n = 2x3y. Au terme du calcul, le PGCD s'affiche en exposant de 5 :
2x3y → ... → 5PGCD[x,y] - Déterminer le plus petit parmi deux entiers est possible sur base de 3 instructions, F = {5/6, 1/2, 1/3} :
2x3y → ... → 5Min[x,y]
Un programme similaire, F = {5/6, 5/2, 5/3} calcule le plus grand parmi deux entiers :
2x3y → ... → 5Max[x,y] - L'échange du contenu de deux registres est possible sur base de 7 instructions, F = {55/14, 7/11, 13/7, 34/39, 13/17, 1/13, 3/5} :
2x3y7 → ... → 2y3x
Calculs de fonctions
- Le programme, F = {13/11, 133/85, 17/19, 23/17, 1015/69, 23/29, 31/23, 111/217, 31/37, 13/31, 17/26, 33/2, 1/13, 1/5}, calcule n'importe quel élément de la suite de Fibonacci, {0, 1, 1, 2, 3, 5, 8, ...}, selon le schéma :
2x → ... → 3fib[x] - Le programme, F = {115/38, 19/23, 17/19, 4147/51, 17/29, 31/17, 259/155, 41/31, 129/481, 37/43, 17/37, 47/533, 41/47, 53/41, 177/583, 53/59, 61/53, 67/427, 1/61, 355/469, 67/71, 17/67, 57/2}, calcule la factorielle, x!, d'un entier donné :
2x → ... → 3x!
Programme universel
Les programmes qui précèdent sont équivalents à autant de machines de Turing dédicacées au calcul d'une fonction particulière. Il est possible de concevoir un programme unique, capable de calculer toute fonction calculable (jouant, en Fractran, le rôle d'une machine de Turing universelle). Ce programme s'écrit :
F = {583/559, 629/551, 437/527, 82/517, 615/329, 371/129, 1/115, 53/86, 43/53, 23/47, 341/46, 41/43, 47/41, 29/37, 37/31, 37/31, 299/29, 47/23, 161/15, 527/19, 159/7, 1/17, 1/13, 1/3}
L'ensemble des fonctions calculables par programmes étant dénombrable, il peut être indicé par un paramètre entier, k. On a que si fk(n) = m, alors le programme fournit : k 22^n → ... → 22^m.
L'article fondateur de Conway présente le début du catalogue des fonctions, fk(n). Sans grande surprise, les premières fonctions sont largement triviales : f1(n) = n est l'identité, f256(n) n'est définie que pour n=3 (f256(3)=4) et f2268945(n) = n+1.
Algorithmes compte-gouttes
L'universalité calculatoire de Fractran garantit qu'il est capable d'énumérer des listes, finies ou infinies, de nombres reliés par une propriété commune :
- Suite de Collatz
Pour rappel, cette suite est construite itérativement au départ de n'importe quel entier, n, faisant suivre tout entier, m, de m/2 si m est pair et de (3m+1)/2 sinon. On a conjecturé qu'elle retombe invariablement à la valeur, m=1. Le programme suivant, dû à Kenneth Monks, F = {1/11, 136/15, 5/17, 4/5, 26/21, 7/13, 1/7, 33/4, 5/2, 7/1}, appliqué à 2n calcule une suite dont on ne retient que les puissances de 2 : les exposants sont les termes de la suite démarrant à n. - Suite des nombres premiers
Le programme, F = {17/91, 78/85, 19/51, 23/38, 29/33, 77/29, 95/23, 77/19, 1/17, 11/13, 13/11, 15/2, 1/7, 55/1}, appliqué à, n = 2, passe successivement, sans jamais s'arrêter, par toutes les puissances de 2, 2p où p est premier. Conway a publié une description abrégée du fonctionnement de l'algorithme sur ce forum.
Décimales de pi
Le programme, F = {365/46, 29/161, 79/575, 679/451, 3159/413, 83/407, 473/371, 638/355, 434/335, 89/235, 17/209, 79/122, 31/183, 41/115, 517/189, 111/83, 305/79, 23/73, 73/71, 61/67, 37/61, 19/59, 89/57, 41/53, 833/47, 53/43, 86/41, 13/38, 23/37, 67/31, 71/29, 83/19, 475/17, 59/13, 41/291, 1/7, 1/11, 1/1024, 1/97, 89/1}, basé sur la formule de Wallis, est censé agir sur la donnée 2n pour produire 2pi[n] comme première puissance de 2, où pi[n] est la nème décimale de pi. Ce programme ne fonctionne malheureusement pas, à cause d'une erreur, jamais corrigée (avis aux amateurs !), probablement au niveau de l'encodage de la donnée, n. Même s'il fonctionnait, il serait d'une lenteur désespérante.
Une variante aisée du tour de Cheney
Attribué à William Fitch Cheney (1831-1879), ce tour de cartes refait régulièrement surface dans les magazines spécialisés. Jean-Paul Delahaye a fait une synthèse des variantes existantes dans une de ses chroniques mensuelles de la revue, Pour la Science (02/2006). Exempt de tout subterfuge, ce tour n'a rien de magique : il maximise le transfert d'information lors de l'échange d'un nombre donné de cartes discernables entre deux partenaires, dénommés Maurice, le magicien, et Alice, son assistante (Le tour fonctionne pareillement si Marie est la magicienne et Albert l'assistant). Quelle que soit la variante, le jeu traditionnel de 52 cartes est remplacé par un jeu de, N, cartes numérotées de 0 à N-1. Celle que nous proposons ici utilise N = n! + n cartes et elle présente l'intérêt de réduire l'intervention mathématique à sa plus simple expression.
La numération factoradique
En arithmétique, l'encodage des entiers se fait habituellement dans une base fixe, b, selon les puissances de b et les chiffres autorisés vont de 0 à b-1. La base 10 est habituelle (chiffres de 0 à 9) mais la base 2 (chiffres binaires 0 et 1) est également d'un usage fréquent. D'autres systèmes de numération existent cependant qui se révèlent intéressants dans certains cas précis. Tel est le cas du système factoradique. Tout entier naturel, x, peut être décomposé d'une seule façon sous la forme, x = cmm! + cm-1(m-1)! + ... + c11!, où les chiffres, cj, vont de 0 à j. Par exemple, 20 = 3 3! + 1 2! + 0 1!. Nous noterons la succession des chiffres entre crochets comme dans l'exemple, 20 = [3,1,0]. Ce système exotique autorise une numérotation simple des permutations de n symboles initialement rangés dans l'ordre naturel, par exemple (si n=4), a < b < c < d.
Il existe 4! = 24 permutations distinctes des symboles, a, b, c, et d. Les voici rangées dans l'ordre lexicographique et numérotées de 0 à 23 :
| ( a b c d ) 0 | ( a b d c ) 1 | ( a c b d ) 2 | ( a c d b ) 3 | ( a d b c ) 4 | ( a d c b ) 5 |
| ( b a c d ) 6 | ( b a d c ) 7 | ( b c a d ) 8 | ( b c d a ) 9 | ( b d a c ) 10 | ( b d c a ) 11 |
| ( c a b d ) 12 | ( c a d b ) 13 | ( c b a d ) 14 | ( c b d a ) 15 | ( c d a b ) 16 | ( c d b a ) 17 |
| ( d a b c ) 18 | ( d a c b ) 19 | ( d b a c ) 20 | ( d b c a ) 21 | ( d c a b ) 22 | ( d c b a ) 23 |
La numération factoradique permet de retrouver rapidement quelle permutation occupe le kième rang, dans ce tableau, et inversement quel rang y occupe une permutation donnée :
- Pour trouver la permutation de rang, k, il suffit de décomposer l'entier, k, en numération factoradique, comme dans l'exemple, k = 20 = [3,1,0]. La 20ième permutation de la liste ( a b c d ) s'obtient en sélectionnnant, dans l'ordre, le symbole de rang 3 (d) - attention le rang le plus à gauche se note 0 -, puis de rang 1 parmi ceux qui restent (b), puis celui de rang 0 parmi ceux qui restent (a), enfin celui qui reste seul (c). Au bilan, la 20ième permutation de ( a b c d ) se note, ( d b a c ).
- Pour trouver l'indice d'une permutation donnée, par exemple ( d b a c ), il suffit de compter (dans l'ordre !) combien d'éléments suivent le 1er symbole (d) et lui sont inférieurs, idem pour le 2ième symbole (b) et idem pour le 3ième, a. On trouve [3,1,0] qui sont les chiffres factoradiques de l'indice cherché, soit, k = 3 3! + 1 2! + 0 1! = 20. On note que, dans ce système, ( a b c d ) porte le numéro 0 et que (d c b a ) porte le numéro 4!-1 = 23. Le lecteur vérifiera la pertinence du tableau ci-dessus.
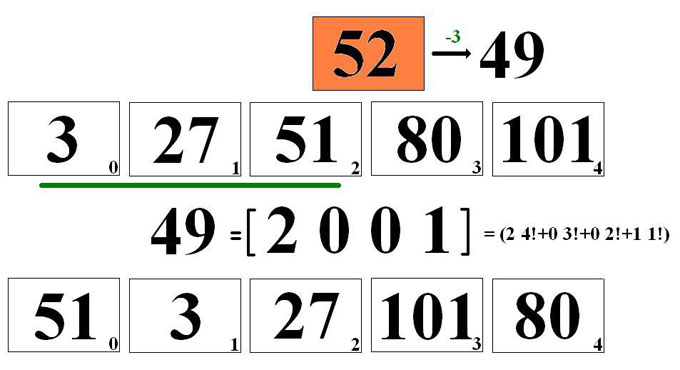
Le tour des 9, 28, 125, 726, ..., cartes
Nous l'illustrons dans le cas n=5. n! + n = 125 cartes, portant chacune un numéro différent, de 0 à 124, sont soigneusement mélangées. Alice tire n+1 = 6 cartes au hasard, soit (3 27 51 52 80 101) et elle en détache une quelconque, appelons-la x = 52, qu'elle dissimule. Elle tend à Maurice les 5 cartes restantes judicieusement empilées dans un ordre à définir. C'est le coeur de la transmission d'information : Maurice sait que les cartes étaient initalement en nombre 125 et que la carte mystère ne peut pas être une de celles qu'Alice lui tend. Au bilan il reste 120 possibilités. Il faut donc qu'Alice dispose de 120 éléments distincts d'information. Or 120 = 5! est précisément égal au nombre des permutations des 5 cartes qui constituent la pile transmise par Alice à Maurice. Il suffit donc que l'empilement corresponde au numéro d'ordre de la permutation utilisée.
L'encodage
La carte mystère porte le numéro, x = 52. Toutefois 52 n'est pas nécessairement l'entier qu'il convient de faire passer à Maurice, c'est en fait, x - y, où y = 3 désigne le nombre de cartes montrées à Maurice et de rang inférieur à x. C'est donc le nombre, 52-3 = 49, qu'Alice doit encoder en numération factoradique. En appliquant l'algorithme ci-dessus, elle trouve 49 = [2, 0, 0, 1], ce qui correspond à la permutation (51 3 27 101 80). C'est dans cet ordre qu'Alice tend les cartes à Maurice.
Le décodage
La tâche de Maurice est plus facile (C'est d'ailleurs pour cela que le magicien est l'homme !). Maurice reçoit un paquet de n = 5 cartes qui se présentent dans l'ordre (51 3 27 101 80). Il lui est facile de voir que cette permutation porte le numéro d'ordre, z = 49. Cet entier, z, est presque le numéro, x, cherché : il faut encore passer les cartes en revue (dans l'ordre !) en ajoutant 1 à z tant qu'il reste dans la pile des nombres plus petits que z réactualisé. Le résultat final désigne le rang, x, de la carte mystère. On trouve successivement : z = 49, 50 (à cause de la présence de 3), 51 (à cause de la présence de 27) et finalement 52 (à cause de la présence de 51). La carte mystère porte le numéro 52.
Devinez l'entier !
Ce jeu un brin académique, entre deux partenaires nommés A et B, offre l'occasion de réfléchir à quelques concepts liés aux théories des probabilités et de l'information. Il se pose informellement de la manière suivante :
A sélectionne "au hasard" un entier positif, n, à charge pour B de le deviner le plus rapidement possible. Pour progresser dans sa recherche, B ne peut poser à A que des questions binaires de son choix, auxquelles A répond honnêtement, par oui ou par non.
Présenté en ces termes, le problème est mal posé car son énoncé est imprécis sur un point essentiel : il ne dit pas ce que signifie, pour A, la sélection d'un entier au hasard. On pourrait penser à la méthode suivante : A enferme des boules numérotées dans une urne, agite celle-ci consciencieusement et puise une boule donc un entier au hasard. Cette manière de faire n'est recevable que si le nombre des boules est fini, autrement dit si l'intervalle des entiers disponibles pour le tirage aléatoire est lui aussi fini, disons [1, N]. Encore faut-il préciser si l'urne contient exactement N boules numérotées chacune de 1 à N sans répétion ou si, au contraire, certains numéros sont présents plusieurs fois voire d'autres éventuellement absents (Dans la suite, on a remplacé l'urne et les boules par une cible circulaire et un jeu de fléchettes). On formalise ces exigences de la manière suivante : il faut que A renseigne B sur
- l'intervalle dans lequel il travaille, [1, N] s'il est fini, et [1, Infini], dans le cas contraire et de
- la densité distributionnelle, g(n), des probabilités qu'il utilise, favorisant éventuellement certains entiers par rapport à d'autres.
-
Le cas particulier suivant, classique et inoffensif, considère la densité homogène sur l'intervalle fini, [1, N] :
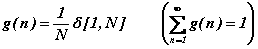
L'information manquante vaut ℓg(N) bits (formule de Shannon), ce qui autorise à penser qu'une stratégie existe, pour B, lui permettant de deviner l'entier inconnu en Ceil[ℓg(N)] questions binaires. Cette stratégie porte le nom de dichotomie binaire; on la rappelle dans le cas, N=32=25, où 5 questions devraient suffire. A chaque étape, on réduit l'intervalle possible [a, b] de moitié, en posant la question, n > (a+b-1)/2 ? Voyons cela sur l'exemple, n = 25 :
- 1ère question : n>16 ? Réponse : OUI = 1 (Il reste les entiers allant de 17 à 32)
- 2ème question : n>24 ? Réponse : OUI = 1 (Il reste les entiers allant de 25 à 32)
- 3ème question : n>28 ? Réponse : NON = 0 (Il reste les entiers allant de 25 à 28)
- 4ème question : n>26 ? Réponse : NON = 0 (Il reste les entiers 25 et 26)
- 5ème question : n=25 ? Réponse : OUI = 1 (n = 25, notez que 25 se note 11001 en binaire)
L'exemple N=32 fonctionne particulièrement bien parce que 32 est une puissance de 2 donc l'information manquante est entière dans ce cas (elle vaut 5 bits). Lorsque N n'est pas une puissance de 2, la dichotomie binaire demeure la stratégie optimale avec la nuance suivante. Supposons N=17, l'information manquante vaut, à présent, ℓg(N)=4.08746 bits. La stratégie binaire précédente devine certainement l'entier, n, en 5 questions (Après tout, qui peut le plus peut le moins) mais elle fait mieux, en moyenne, soit en 71/17 = 4.17647 questions binaires, ce qui nous rapproche de la limite de Shannon. Il suffit, pour le voir, d'examiner tous les cas de figures et de se rendre compte que 4 questions suffisent dans 14 cas sur 17 tandis qu'il en faut 5 dans 3 cas sur 17 seulement. -
Le cas infini est nettement plus délicat. Commençons par remarquer qu'il n'est plus possible, dans ce cas, de considérer que tous les entiers sont équiprobables : la fonction de distribution, g(n), ne serait pas normalisable à l'unité. Une procédure effective permettant à A de sélectionner au hasard un entier arbitrairement grand n'est envisageable que selon un hasard non uniforme qui pénalise les grands entiers. Plus formellement, la fonction de distribution doit être suffisamment décroissante, lorsque n s'éloigne à l'infini, afin de garantir la normalisation de g(n). Une décroissance selon la loi, g(n)=1/n, ne suffit pas car la série harmonique diverge, par contre, une décroissance selon la loi, g(n)=1/n2, convient certainement. Etudions ce cas :
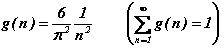
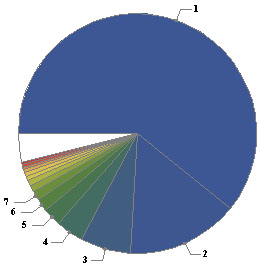
L'information manquante vaut dans ce cas précis (formule de Shannon) :
Il ne faudrait pas en conclure que 3 questions binaires devraient suffire à B pour découvrir l'entier inconnu, à tous coups, d'ailleurs cela n'aurait aucun sens : tous les entiers étant possibles sans restriction de taille, il ne faut pas espérer deviner tous les cas en un nombre fini de questions. Ce que la formule de Shannon laisse espérer, dans le cas infini, est différent, à savoir qu'il existe une stratégie qui, en moyenne, devine l'entier caché en approximativement 2.4 questions binaires. Autrement dit, il se fera certainement que 10 ou 20 questions s'avèrent nécessaires mais ces cas coûteux seront rares. Cette stratégie optimale moyenne existe effectivement et elle est à nouveau basée sur la dichotomie équitable que voici dans le détail.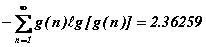
Dans la série infinie suivante, la partition la plus équitable se note :
d'où la 1ère question posée par B :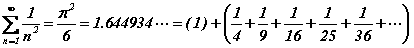
n>1 ? Une réponse négative ne laisse la place qu'à une seule valeur pour n, soit n=1. Dans ce cas favorable, une seule question a suffi.
Si la réponse à la première question est positive, il convient de poursuivre en partitionnant équitablement le reste de la série infinie. On trouve :
d'où la 2ème question posée par B :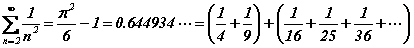
n>3 ? Une réponse négative ne laisse la place qu'aux deux valeurs, n=2 et n=3, d'où une question supplémentaire suffit pour trancher. Au bilan, dans ce cas favorable, 3 questions ont suffi sinon il convient de poursuivre la recherche avec la partition suivante :
d'où la 3ème question posée par B :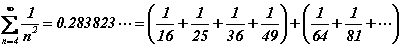
n>7 ? Une réponse négative laisse la place aux quatre valeurs, n=4, n=5, n=6 et n=7, d'où deux questions supplémentaires suffisent pour trancher. Au bilan, dans ce cas favorable, 5 questions suffisent sinon il convient de poursuivre la recherche avec la partition suivante.
Poursuivant la manoeuvre avec les restes successifs,
on trouve que la kième question revêt la forme simple :
n>2k-1 ? Une réponse négative ne laisse la place qu'à 2k-1 valeurs pour n, allant de n=2k-1 à n=2k-1, inclus, d'où k-1 questions supplémentaires suffisent pour trancher; au bilan, cela fait 2k-1 questions dans ce cas favorable.
Note : cette affirmation repose sur la double inégalité remarquable, donnée sans démonstration :
Au bilan, le nombre moyen de questions binaires que B doit poser se calcule comme suit :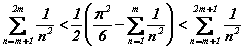
Il n'y a pas lieu de s'étonner que ce nombre soit légèrement supérieur à la valeur théorique de Shannon (2.36529) : les partitions opérées successivement ne sont qu'approximativement égales et cela a un prix bien connu en théorie de l'information.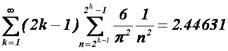
On le voit, la meilleure stratégie, sans être particulièrement imaginative, est plutôt efficace puisqu'elle règle le problème en 2.45 questions, en moyenne. Cette belle performance résulte du fait qu'on a utilisé une stratégie tenant compte de la décroissance de, g(n), qui oblige A à choisir plus fréquemment des entiers de petite taille. Notez que la stratégie naïve consistant à poser comme kième question, "L'entier cherché vaut-il k ?" est loin d'être optimale, le temps moyen devenant infini : c'est la conséquence de la divergence de la série harmonique. -
Posons à présent que A veuille compliquer la tâche de B au maximum : il y parvient en utilisant une distribution, g(n), dont la normalisation repose sur une série convergeant vers 1 le plus lentement possible. Il est remarquable qu'une telle distribution - dite universelle - existe, qui se situe à la limite de la convergence et de la divergence. Elle est basée sur une suite de résultats analytiques concernant les séries infinies, que l'on rappelle :
-
Les séries infinies suivantes divergent toutes mais de plus en plus lentement :
Par contre, les séries infinies suivantes convergent toutes mais de plus en plus lentement :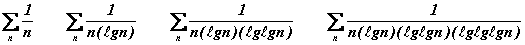
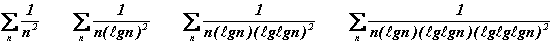
-
On en déduit que la série infinie suivante se situe à la frontière qui sépare la convergence de la divergence :
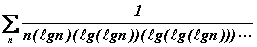
Voyons le rapport que cette série entretient avec le tirage aléatoire d'un entier non borné. Commençons par noter que ce tirage ne peut reposer sur le principe naïf suivant : tout entier positif possédant une traduction binaire en termes de 0 et de 1, on lancerait une pièce de monnaie et la suite des tirages successifs pile (=1) ou face (=0) construirait (de droite à gauche) l'entier désiré. Cette procédure ne fonctionne pas pour la raison évidente qu'elle ne comporte aucune instruction d'arrêt : après avoir tiré, disons 10011, comment savoir s'il faut s'arrêter et accepter l'entier correspondant (19) ou continuer à lancer la pièce? Préfixer l'écriture binaire de 10011 par une étiquette binaire, 100, qui annoncerait la longueur (4) de sa partie significative (le 1 initial ne l'est pas) ne convient pas davantage car rien dans la succession des chiffres tirés, 100 00011, ne distinguerait la fin de l'étiquette du début du nombre proprement dit. La solution à ce case-tête est l'étiquetage répétitif : on préfixe bien la représentation binaire (amputée de son 1 initial non significatif) de n=10011 par une étiquette, 100, qui annonce la longueur (4) puis on fait de même avec une deuxième étiquette, 10, qui annonce la longueur (2) de la partie significative de la première et ainsi de suite jusqu'à tomber sur une étiquette de longueur 2 (=10) ou 3 (=11), ce qui ne peut manquer de se produire (Cette dernière étiquette ne peut être amputée de son 1 initial pour des raisons évidentes de décodabilité). On termine la procédure en préfixant le tout par autant de 0 que le nombre total d'étiquettes consommées, ce qui donnerait dans notre exemple, 00 10 00 0011, où les espaces servent seulement à faciliter votre lecture. Au bilan, le code préfixe de l'entier n=19 se note 00 10 00 0011 (Le décodage inverse est facile : ne pas oublier de rajouter les 1 initiaux à chaque étape). La procédure peut paraître coûteuse aux petites valeurs de n mais, asymptotiquement, on verra qu'il n'y a pas moyen de faire mieux. On trouvera, en annexe, le détail des procédures décrites (Notebook Mathematica).
Le lecteur vérifiera, sur quelques valeurs de n, que la procédure fonctionne sur tous les entiers supérieurs à 3. Les entiers 1, 2 et 3 sont encodés séparément en commençant par un 1, ce qui empêche toute confusion. Au bilan, on trouve la liste suivante des codes préfixes universels des entiers positifs :
Spref = {
s1 ≡ 10, s2 ≡ 110, s3 ≡ 111, s4 ≡ 01000, s5 ≡ 01001, s6 ≡ 01010, s7 ≡ 01011,
s8 ≡ 011000, s9 ≡ 011001, s10 ≡ 011010, s11 ≡ 011011, s12 ≡ 011100, s13 ≡ 011101, s14 ≡ 011110, s15 ≡ 011111,
s16 ≡ 0010000000, s17 ≡ 0010000001,..., s31 ≡ 0010001111,
s32 ≡ 00100100000, ..., s63 ≡ 00100111111,
... }
La suite, S, est affichée de telle façon que sa structure numérique devienne apparente : elle contient 1 code de longueur 2, 2 codes de longueur 3, 4 codes de longueur 5 et plus généralement 2k codes de longueur ℓ(k), où la suite ℓ(k), croît comme (k = 0, 1, 2, 3, ...) :
ℓ(k) = { 2, 3, 5, 6, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 44, …}.
La suite, S, possède trois propriétés remarquables et essentielles pour le but poursuivi :
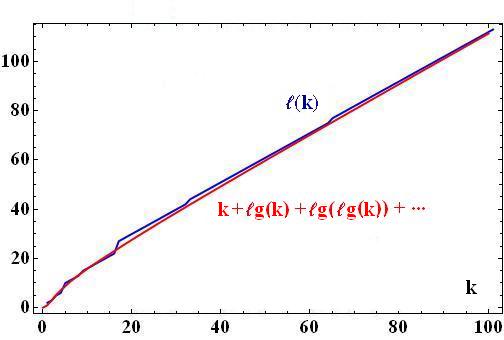
- Les longueurs de codes, ℓ(k), croissent asymptotiquement comme : ℓ(k) = k + ℓg(k) + ℓg(ℓg(k)) + ℓg(ℓg(ℓg(k))) + ... . C'est la conséquence naturelle du fait que chaque étiquette allonge le code de n d'une valeur égale au logarithme de l'étiquette précédente, la première étiquette l'allongeant du logarithme de n.
- La suite S est préfixe, ce qui signifie qu'aucun code d'entier n'est préfixe d'un autre code. C'est cette propriété qui justifie l'arrêt des tirages aléatoires dès qu'un terme de la suite est rencontré; il ne servirait, en effet, à rien de poursuivre.
- La suite S est complète, ce qui signifie que tout tirage aléatoire est assuré de se terminer sur un code faisant partie de la suite.
-
Les séries infinies suivantes divergent toutes mais de plus en plus lentement :
On montre, en théorie de l'information qu'un code préfixe et complet satisfait l'égalité de Kraft :
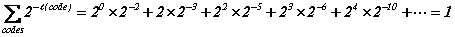
On peut vérifier directement ce résultat en regroupant astucieusement les termes de cette série, de n=2k à n=22^k -1 : les probabilités cumulées valent exactement 2-k, livrant une progression géométrique de raison, 1/2, convergent vers 1.
La stratégie optimale que B doit suivre se dégage à présent sur base d'une dichotomie binaire :
- 1ère question : n>3 ? Une réponse négative laisse la place aux trois valeurs, n=1, n=2 et n=3, d'où deux questions supplémentaires suffisent certainement pour trancher. Au bilan, dans ce cas favorable, 1+2=3 questions suffisent sinon (n>3) il convient de poursuivre la recherche avec la partition suivante.
- 2ème question : n>15 ? Une réponse négative laisse la place aux douze valeurs, de n=4 à n=15, d'où quatre questions supplémentaires suffisent certainement pour trancher. Au bilan, dans ce cas favorable, 2+4=6 questions suffisent sinon (n>15) il convient de poursuivre la recherche avec la partition suivante.
- 3ème question : n>65535 ? Une réponse négative laisse la place aux 65520 valeurs, de n=16 à n=65535, d'où seize questions supplémentaires suffisent certainement pour trancher. Au bilan, dans ce cas favorable, 3+16=19 questions suffisent sinon il convient de poursuivre la recherche avec la partition suivante.
Poursuivant la manoeuvre avec les restes successifs, on trouve que la kième question revêt la forme simple :
- kème question : n>2^2^...k symboles ^^2 - 1 ? Une réponse négative "ne laisse la place qu'aux" valeurs de n, allant de n = 2^2^...(k-1) symboles ^^2 à n = 2^2^...k symboles ^^2-1, inclus, d'où 2^2^...(k-1) symboles ^^2 questions suffisent (!) pour trancher. Au bilan dans ce cas "favorable", k + 2^2^...(k-1) symboles ^^2 questions "suffisent" à ce stade.
Vu que 2-ℓ(code[n]) vaut précisément la probabilité de tirer au sort le code de n, on voit que l'égalité de Kraft remplit la condition de normalisation pour la densité de probabilité, g(n)=2-ℓ(code[n]).
En adoptant cette distribution, A est assuré de compliquer au maximum la tâche de B précisément parce que c'est la distribution la plus lentement décroissante parmi toutes celles qui sont envisageables. Le fait que la conditon de normalisation se situe à l'extrême limite de la convergence a une conséquence dramatique pour B : le nombre moyen de questions binaires tend vers l'infini. Autrement dit, B ne peut accepter aucun pari proposé par A sans être assuré de se ruiner, à terme.
Une dernière remarque : lorsque B n'est pas informé de la loi, g(n), adoptée par A, il est contraint de faire comme si c'était la distribution universelle. Procéder autrement équivaudrait à introduire un élément d'information parasite de nature à privilégier abusivement les petits entiers. La seule attitude prudente, qui ne présuppose rien d'inconnu, consiste à adopter la loi g(n) la moins porteuse d'information, celle qui décroît asymptotiquement le plus lentement possible sans compromettre la normalisation. Cette loi c'est la distribution universelle ou toute autre distribution asymptotiquement équivalente.
Fonctions de Walsh et compression avec perte
Autant l'analyse de Fourier (discrète) des signaux (digitaux) est connue autant celle de Walsh l'est peu. Le principe de base est similaire : il s'agit de trouver un ensemble orthogonal complet de fonctions permettant de développer n'importe quelle suite (digitale), de longueur 2s (s entier positif), en séries des fonctions de base. Alors que l'analyse de Fourier recourt à des fonctions de base trigonométriques, héritées de l'analyse infinitésimale, l'analyse de Walsh respecte le créneau binaire : ses fonctions de base ne prennent que deux valeurs, usuellement -1 et +1, pour des raisons de symétrie.
Il y a mille façons d'introduire les fonctions de Walsh mais l'approche récursive de Hadamard semble la plus simple. On commence par définir la suite des matrices de Hadamard 2sx2s, pour s = 0, 1, 2, …, comme suit :
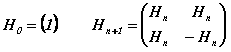
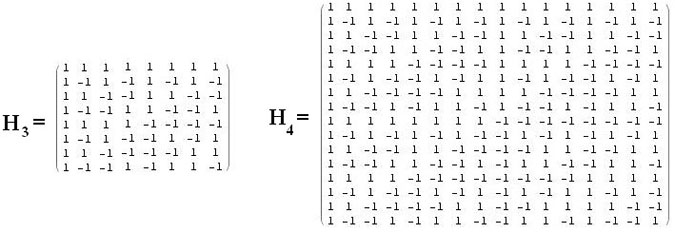
Voici deux matrices de Hadamard, de tailles raisonnables (respectivement s=3 et s=4) :
Pour une valeur donnée de s, les fonctions de Walsh sont définies par les vecteurs lignes (ou colonnes car les matrices de Hadamard sont symétriques) de Hs. Voici les graphes de ces fonctions de Walsh dans les deux cas pris en exemple :
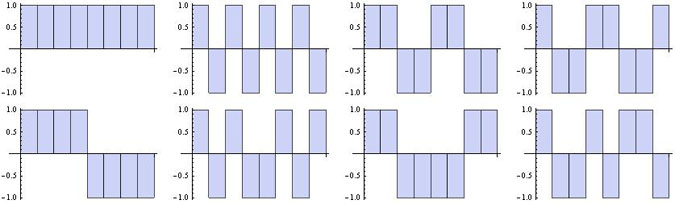
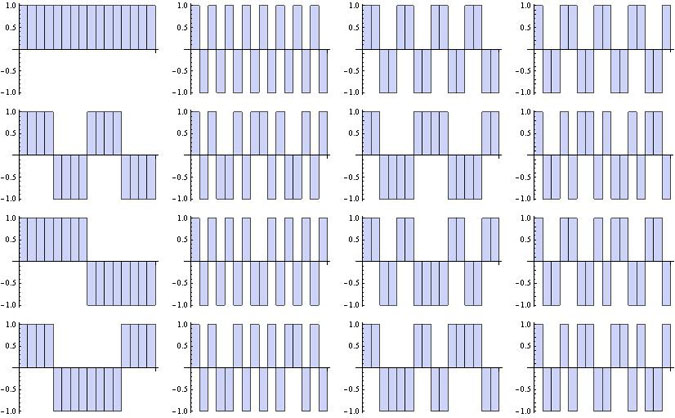
La méthode de Hadamard énumère les 2s fonctions de Walsh, Ws,i (i = 1, 2, ..., 2s), dans un ordre qui n'est pas nécessairement celui qui prévaut dans d'autres approches mais, au bilan, elles sont toutes bien présentes. Toutes sont orthogonales, au sens du produit scalaire habituel, et le carré de leur norme vaut 2s. Autrement dit, les fonctions, 2-s/2Ws,i forment un ensemble orthogonormé qui est de plus complet : toute fonction, V, étagée sur l'ensemble {-1, +1}, par exemple la fonction {1,1,1,1,1,1,-1,-1} (s=3), est décomposable en termes de fonctions de Walsh, W3,i, et les coefficients du développement sont donnés par les produits scalaires, V.W3,i. Cela résulte de l'identité :
(2-s/2Hs.V)T.(2-s/2Hs) = V
Les fonctions de Walsh ainsi définies sont unidimensionnelles. Toute fonction de deux variables, étagée sur l'ensemble {-1, +1}, peut être développée en produits de fonctions de Walsh, 2-sWs,iWs,j (i,j = 1, 2, ..., 2s). Un exemple particulièrement intéressant est celui d'une image pixélisée sur une trame 2sx2s.
Décomposition exacte d'une image en fonctions de Walsh
La manière la plus commode de représenter les fonctions de Walsh à deux dimensions consiste à afficher l'image Noir & Blanc de leur trame. Par exemple, dans le cas, s = 3, les 22s (= 64) fonctions, Ws,iWs,j, présentent les trames suivantes :

L'orthogonormalité peut être visualisée en superposant deux trames quelconques et en multipliant les valeurs pixélisées de mêmes positions (+1 si pixel blanc, -1 sinon) et en sommant sur les 64 pixels : on trouve systématiquement 0 si les trames sont distinctes et 2s (= 8) si elles sont identiques. Toute image binaire (Noire & Blanche) peut être décomposée en termes de ces fonctions de base.
Les images binaires qui nous servent de modèles sont celles de caractères alphabétiques, pixélisées sur une trame 64x64 (s = 6), facilement obtenables sur n'importe quel PC en suivant le protocole suivant : démarrer/exécuter/eudcedit/Sélectionner le code/OK/Edition/Copier un caractère/copier coller le caractère choisi, R par exemple, dans n'importe quel programme de dessin (Paint, par exemple). Cela donne :
Une représentation binaire de ce caractère qui convient pour un développement en fonctions de Walsh code les blancs par 1 et les noirs par -1. D'autres conventions sont envisageables mais celle-ci est adoptée par le logiciel Mathematica qui précise, en outre : 0 (ou tout réel inférieur) code un pixel blanc, 1 (ou tout réel supérieur) code un pixel noir et tout réel compris entre 0 et 1 code un niveau de gris.
Le programme Mathematica, joint en en annexe (Notebook Mathematica), décompose l'image du caractère, R, en fonctions de Walsh. En soi cette décomposition semble présenter peu d'intérêt. Toutefois un point retient l'attention : les ordres de grandeur des coefficients du développement décroissent rapidement. Voici, pour fixer les idées, le début de la liste des valeurs absolues des coefficients de Walsh correspondant à l'image de la lettre R, rangés dans l'ordre des valeurs décroissantes :
{3004, 1088, 504, 500, 500, 496, 440, 436, 424, 424, 420, 420, 412, 408, 248, 248, 244, 244, 244, 240, 232, 228, 212, 208, 208, 204, 204, 200, 196, 192, 188, 188, 184, 184, 184, 180, 180, 180, 176, 176, 176, 176, 176, 172, 172, 172, 168, 164, 164, 164, 160, 160, 156, 156, 156, 152, 152, 152, 152, 152, 148, 148, 148, 144, 144, 144, 144, 140, 140, 140, 140, 140, 136, 136, 132, 128, 128, 128, 124, 124, 124, 120, 120, 116, 116, 116, 112, 112, 112, 108, 108, 108, 104, 104, 104, 104, 104, 104, 100, 100, 100, 100, 96, 92, 92, 92, 92, 92, 92, 88, 88, 88, 88, 88, 88, 88, 88, 88, 88, 84, 84, 84, 84, 84, 84, 84, 84, 84, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, ...}
L'idée germe aussitôt de regarder ce qui se passe si on tronque le développement en série de Walsh en ne retenant que les contributions les plus importantes au-delà d'un seuil variable à définir.
Décomposition tronquée d'une image en fonctions de Walsh : compression avec perte
Sans troncature donc sans perte, l'image reconstituée est fidèle à l'original, pixélisé de façon binaire sur {-1, +1}. Si on tronque le développement, des valeurs intermédiaires apparaissent que Mathematica restitue en niveaux de gris, polluant plus ou moins l'image compressée. Si on conserve les 872 (sur 4096) coefficients supérieurs à 20 (en valeur absolue), voici l'image qu'on reconstitue :
Si on conserve les 98 (sur 4096) coefficients supérieurs à 100 (en valeur absolue), voici l'image qu'on reconstitue :
Si on conserve les 27 (sur 4096) coefficients supérieurs à 200 (en valeur absolue), voici l'image qu'on reconstitue :

Si on supprime les niveaux de gris dans les images précédentes, on n'en garde qu'un squelette de moins en moins reconnaissable :

En pratique, conserver 1/16 des coefficients les plus importants (soit 256 sur 4096) suffit largement à maintenir une image nettement reconnaissable. Le taux de compression de 94% est appréciable.
Reste un point à élucider : il est évidemment exclu de trouver une procédure effective qui décide des indices des fonctions de Walsh à conserver dans le développement tronqué de n'importe quelle image choisie au hasard. Par contre, si on se limite à une famille de figures, par exemple l'ensemble des caractères alphabétiques occidentaux, une stratégie envisageable consiste à les recenser préalablement en répertoriant dans une base de données les indices les plus fréquents pour cette famille.
Statistique de la production des machines de Turing binaires simples (MTS)
Il existe beaucoup de présentations équivalentes des machines de Turing (MT) et nous optons pour le formalisme le plus compact, sans instruction explicite d'arrêt, dû à Stephen Wolfram et exposé dans son ouvrage, A New Kind of Science, en abrégé, NKS. Tous les calculs présentés en annexe (Notebook Mathematica) ont été programmés en langage Mathematica en respectant, à peu de choses près, l'ensemble des conventions fixées par Wolfram (sauf que celui-ci numérote bizarrement les états des MT de 1 à s alors que le faire de 0 à s-1 s'avère nettement plus simple; de même il code le déplacement de la tête des MT par -1 ou +1 selon qu'il s'effectue vers la gauche ou vers la droite mais il apparaît clairement à l'usage que les choix 0 et 1 sont préférables).
Une MTS se décrit en fonction de son nombre d'états, s, et de son nombre de caractères, k. On ne limite pas le pouvoir calculatoire des MTS en les restreignant à k=2 caractères, 0 et 1. Dans cette présentation, les MTS sont binaires et elles se décrivent comme suit :
- Une bande, semi-infinie, disons vers la gauche, partitionnée en cellules hébergeant un caractère binaire, 0 (cellule blanche) ou 1 (cellule noire).
- Une tête de lecture-écriture qui se déplace le long de cette bande, une cellule à la fois. Elle se trouve, à tout instant, dans un état, σ, parmi les s états autorisés (σ = 0, 1, ..., s-1), s pouvant prendre n'importe quelle valeur positive, s = 2, 3, 4, ... . La tête est initialement positionnée à l'extrémité droite de la bande, en face de la cellule n=0, et elle se trouve dans l'état σ = 0. Dans les figures qui suivent, l'état, σ, est représenté par l'aiguille d'une horloge qui pointe vers 12σ/s heures.
- Une table d'instructions qui dicte le comportement de la tête à chaque pas discret d'évolution. Ces instructions sont du type, {état actuel, caractère lu} → {nouvel état, caractère écrit, déplacement de la tête}. La machine évolue en respectant cette table : à chaque pas d'évolution, la tête lit le caractère situé en face d'elle et en fonction de l'état interne, elle le remplace par l'un des caractères possibles (éventuellement celui qui a été lu), elle change éventuellement d'état interne et elle se déplace (obligatoirement) d'une cellule vers la gauche (δ=0) ou vers la droite (δ=1). La machine ne s'arrête que lorsque la tête est invitée à dépasser l'extrémité fixe de la bande. Lorsque l'arrêt se produit, la réponse est lue de gauche à droite (la convention inverse serait tout aussi valable), entre la position la plus extrême-gauche atteinte par la tête et l'extrémité fixe.
L'absence d'instruction explicite d'arrêt garantit la concision maximale du formalisme. Certains auteurs incorporent une voire plusieurs instructions d'arrêt à la table d'instructions mais cela est inutile et même carrément redondant (On ne voit, en particulier, pas l'intérêt d'introduire une deuxième instruction d'arrêt lorsque la première a déjà été activée).
Une table comprend 2s instructions. Wolfram les range dans l'ordre immuable suivant (l'instruction en couleur est celle qui est activée en premier lieu) :
| (0,1) → (σ1,κ1,δ1) | (0,0) → (σ2,κ2,δ2) |
|---|---|
| (1,1) → (σ3,κ3,δ3) | (1,0) → (σ4,κ4,δ4) |
| (2,1) → (σ5,κ5,δ5) | (2,0) → (σ6,κ6,δ6) |
| ... | ... |
| (s-1,1) → (σ2s-1,κ2s-1,δ2s-1) | (s-1,0) → (σ2s,κ2s,d2s) |
La numérotation des MT s'effectue comme suit. Chaque triplet, (σj,κj,δj) définit un chiffre en base 4s, conformément au schéma :
| (0, 0, 0) → 0 | (0, 0, 1) → 1 | (0, 1, 0) → 2 | (0, 1, 1) → 3 |
|---|---|---|---|
| (1, 0, 0) → 4 | (1, 0, 1) → 5 | (1, 1, 0) → 6 | (1, 1, 1) → 7 |
| ... | ... | ... | ... |
| (s-1, 0, 0) → 4s-4 | (s-1, 0, 1) → 4s-3 | (s-1, 1, 0) → 4s-2 | (s-1, 1, 1) → 4s-1 |
La suite des triplets de la table, (σ1,κ1,δ1)(σ2,κ2,δ2) ... (σ2s,κ2s,δ2s), définit donc un entier en base 4s qui numérote la machine de Turing sans ambiguïté. Par exemple, la machine binaire à 3 états, d'instructions, (0,1) → (1,0,1), (0,0) → (2,0,0), (1,1) → (0,1,0), (1,0) → (2,0,1), (2,1) → (0,0,0), (2,0) → (1,1,1), porte, en base 4s=12, le numéro 582907, qui résulte du calcul suivant : 5 125+8 124+2 123+9 122+0 12+7 = 1414807, en base 10.
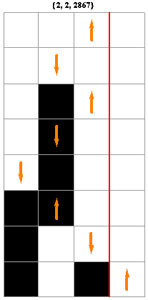
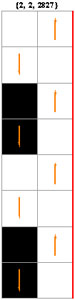
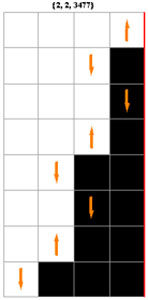
Il existe (4s)2s machines binaires distinctes à s états, soit respectivement, 4096 (s = 2), 2985984 (s = 3), 4294967296 (s = 4), 10240000000000 (s = 5), etc. Avec les conventions adoptées, elles sont numérotées de 0 à 4095, de 0 à 2985983, etc. Ci-contre évoluent trois machines à deux états, choisies parmi les 4096 existantes.
Bien que l'évolution d'une MT se situe entièrement sur la bande unidimensionnelle, une représentation bidimensionnelle qui archive tous les pas de l'évolution s'avère particulièrement parlante.
On remarque que la MT 2867 s'arrête après 7 pas (elle imprime la suite 101), tandis que les MT 2827 et 3477 ne s'arrêtent "visiblement" pas, l'une bouclant et l'autre divergeant. Les esprits chagrins pourraient exiger une démonstration de cette absence d'arrêt, ce qui ne peut se faire que dans un cadre axiomatique adéquat, par exemple celui de l'arithmétique de Peano. Une démonstration par récurrence est effectivement possible tant que s<5.
Les choses se compliquent éventuellement à partir de s = 5 car l'inspection visuelle devient problématique (10240 milliards de machines à prendre en considération) ! Concrètement, la tête de quelques dizaines de machines adopte un comportement erratique impossible à cerner aussi loin que pousse le temp de calcul. Il est, de fait, bien connu que l'arrêt des MT est frappé d'indécidabilité générique sans qu'on puisse connaître le seuil à partir duquel elle se manifeste.
Il est illusoire de croire que l'on pourrait démontrer l'arrêt de chaque machine individuellement en travaillant dans Peano car cette arithmétique est indécidable, au sens de Gödel cette fois, ce qui signifie qu'il existe une infinité de propositions bien formulées (dont l'arrêt des MT) qui ne sont ni démontrables ni réfutables dans ce cadre arithmétique (et pas davantage dans des cadres plus étendus, de la théorie des ensembles par exemple). Personne ne sait aujourd'hui avec certitude si les machines qui posent déjà problèmes dans le cas s=5 s'arrêtent ou ne s'arrêtent pas.
L'ensemble infini mais dénombrable des MT possédant un nombre quelconque, s, d'états et travaillant sur une bande semi infinie, initialement peuplée de 0 (ou de 1) est calculatoirement universel en ce sens qu'il est susceptible d'imprimer n'importe quelle suite finie au terme de son calcul. Toutes les suites ne sont cependant pas imprimées avec des fréquences égales : les suites moins complexes (dans un sens qui reste à préciser, cfr rubrique 7) sont exponentiellement plus souvent imprimées que les autres, conformément au principe d'Ockham. Le calcul des fréquences d'apparition des suites est accessible à un PC banal dans les cas s = 2 et s = 3 et avec un peu de patience, dans le cas s = 4. Ce travail a été envisagé pour la première fois par Hector Zenil dans le cadre de sa thèse de doctorat, effectué sous la direction de Jean-Paul Delahaye, à l'Université de Lille. Notre approche est légèrement différente, qui privilégie la compacité maximale de l'énumération des machines de Turing. En particulier, elle ignore les instructions d'arrêt, surnuméraires dans la présentation de Zenil, avec la crainte qu'une même machine soit comptabilisée plus d'une fois, d'où une statistique faussée. Nos résultats diffèrent d'ailleurs légèrement à cause de cela.
Production des machines binaires simples à deux états
Rien ne s'oppose à ce qu'on épluche consciencieusement le comportement des 4096 machines à s=2 états. On peut diminuer ce nombre en ignorant les MT dont on est sûr qu'elles ne s'arrêtent pas, par exemple, celles dont les instructions activées prévoient systématiquement un déplacement de la tête vers la gauche. De même on identifie facilement une moitié des machines (soit 2048) qui s'arrêtent après un seul pas d'exécution, en imprimant un seul caractère, 0 ou 1. Tout cela est détaillé en annexe.
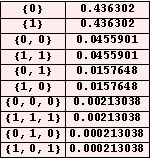
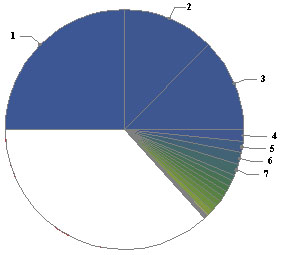
Le résultat des calculs présente une dissymétrie gauche-droite que l'on répare en lisant la réponse deux fois, de gauche à droite puis de droite à gauche. Il présente une autre dissymétrie vis-à-vis de la substitution 0↔1, que l'on répare en faisant tourner les 4096 machines sur une bande initialement noire. En fait, il n'est pas nécessaire de faire les calculs détaillés, il suffit de symétriser les résultats obtenus dans un premier temps. Au bilan, lorsque s=2, on trouve la répartition ci-contre des fréquences.
Pour la petite histoire, les 11 machines les plus actives (encore appelées "Castors affairés") s'arrêtent après 7 pas d'exécution. Ces machines sont également les plus productives, imprimant 3 caractères. Lorsqu'une machine ne s'est pas arrêtée après 7 pas, on a donc l'assurance qu'elle ne s'arrêtera jamais.

Production des machines binaires simples à trois états

On peut recommencer les calculs dans le cas s=3 en respectant le même protocole. Même en écartant les machines qui ne s'arrêtent certainement pas parce que la tête ne cesse de s'éloigner vers la gauche et celles qui s'arrêtent après un seul pas d'exécution, il en reste encore 580608 qui réclament une heure de calcul sur un PC basique. Des raffinements sont cependant possibles qui diminuent sérieusement le temps d'exécution.
Tous calculs faits, on obtient la table ci-contre qui précise la précédente, établie dans le cas s=2. On montre, en annexe, que les 8 machines les plus affairées s'arrêtent après 25 pas d'exécution. Deux machines (1910955 et 2837826) parmi les plus productives (6 caractères) sont dans ce cas.
On note également que les suites ne se classent plus rigoureusement dans l'ordre des longueurs croissantes : par exemple, les suites {0,0,0,0,0} et {1,1,1,1,1} viennent s'intercaler au beau milieu des suites de longueur 4, c'est la conséquence d'une complexité algorithmique moindre. Le lecteur intéressé peut se reporter à l'article de Zenil et Delahaye ou poursuivre par l'étude du point 7 qui remplace avantageusement l'étude statistique par l'exploration méthodique de l'impression des suites binaires.
Compression sémantique des suites binaires courtes par MTS (Attention la numérotation des MTS diffère légèrement de celle au point 6 !)
Aucun algorithme ne peut prétendre compresser sans pertes toutes les suites (binaires ou autres) : compresser une suite binaire, c'est la remplacer sans ambiguïté par une suite plus courte qu'elle. Si on code une suite longue par une suite courte, que va-t-on faire de celle-ci sinon la remplacer par une suite plus longue qu'elle ? Autrement dit, un algorithme ne peut prétendre compresser sans pertes certaines suites qu'à la condition d'en dilater d'autres. Dès lors pourquoi s'intéresser à la compression ? La réponse tient en une ligne : toutes les suites ne se valent pas. Quel que soit le domaine d'activité, scientifique mais aussi littéraire ou musical, les suites aléatoires (de chiffres, de lettres ou de notes) n'intéressent pas grand monde et ce sont elles qui sont sacrifiées sur l'autel de la compression. Vu que les suites aléatoires sont incomparablement plus nombreuses, on parvient à ce compromis acceptable qu'une bonne méthode de compression est efficace sur les suites structurées au détriment des suites aléatoires qui sont légèrement dilatées.
La science peut être vue comme l'art de compresser les données numériques accumulées à la faveur d'observations. Mais de quelle compression veut-on parler : syntaxique (Shannon) ou sémantique (Kolmogorov) ? La suite des positions de la planète Mars dans le ciel, repérées à intervalles temporels réguliers, est certainement compressible au sens de Shannon car ces positions varient peu d'un jour à l'autre, d'où une répétition probable des premiers chiffres significatifs, signe d'une redondance syntaxique. Cependant cette compression, entièrement automatisable jusqu'à la limite de Shannon par des procédures connues, est encore très éloignée de la limite sémantique de Kolmogorov. Les physiciens présument que l'encodage de la résolution des lois de Newton sur un jeu de conditions initiales bien choisies approche sinon rejoint la limite sémantique de la description par programme des systèmes planétaires. Autrement dit, les lois de la nature compressent (sémantiquement) au mieux les données issues de l'observation. Le lecteur totalement néophyte en théorie de l'information peut souhaiter se reporter aux exposés préliminaires, disponibles sur ce site.
L'ensemble des suites binaires finies est récursivement énumérable dans l'ordre naturel :
L'entier qui caractérise une suite ne contient ni plus ni moins d'information que cette suite, d'ailleurs son écriture binaire est identique sauf l'absence du chiffre 1 initial, non significatif chez les entiers binaires positifs. Toute procédure visant à compresser les suites revient à réécrire les suites binaires dans un autre ordre, ce qui a effectivement pour résultat d'en compresser certaines et d'en dilater d'autres. Il y a, a priori, une infinité de façons de réordonner les suites mais celle qui nous intéresse doit privilégier les suites structurées par un programme court au détriment des suites aléatoires. Qui dit programme, dit machine de Turing, d'où l'idée de baser la compression scientifique sur l'aptitude des machines de Turing à produire les suites sur base du plus petit nombre d'instructions.
La complexité, K, d'une suite, S, est traditionnellement définie comme la longueur du plus court programme préfixe binaire alimentant une machine de Turing universelle (MTU) donnée, qui en provoque l'arrêt et imprime S. Ce programme minimum représente la meilleure compression (sémantique) de la suite imprimée. Formellement cela pourrait s'écrire :
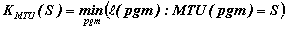
Pour exploiter cette définition, il faudrait au moins se mettre d'accord sur une MTU, par exemple celle que Minsky a conçue dans les années 1960. Cependant les choses ne sont pas si simples car la MTU doit être (libre de tout) préfixe, autrement dit, les programmes qui l'alimentent doivent être auto-délimités (= uniquement décodables). Cela implique que toutes les suites binaires ne constituent pas un programme valable pour une MTU préfixe. Or s'il n'est pas difficile de proposer un codage préfixe complet des suites binaires, il est beaucoup plus délicat de démontrer que la MTU (par exemple celle de Minsky) demeure universelle pour ce choix restreint de suites-programmes.
Il est beaucoup plus simple de revenir vers les machines de Turing simples (MTS par opposition à MTU), alimentées initialement par une bande "vierge" : elles sont également collectivement universelles, à condition de n'en oublier aucune. Le modèle de ces MTS a été rappelé à la rubrique 6 ci-dessus, toutefois nous souhaitons y apporter quelques retouches. Les conventions adoptées par Wolfram sont malheureuses au niveau de l'ordre utilisé pour les énumérer, qui voit les états monter quand les caractères descendent. Il est plus judicieux que les états descendent comme les caractères : on a alors la certitude que les premières MTS à (s+1) états, reproduisent les comportements des machines à s états. Autrement dit, si on décide de se pencher sur l'étude des MTS à moins de 5 états, il n'est pas nécessaire de se préocupper des machines à 2 ou 3 états, celles-ci sont automatiquement reprises au début de l'étude des machines à 4 états. Voici l'ordre modifié dans la table d'instructions des MTS :
| (s-1,1) → (σ1,κ1,δ1) | (s-1,0) → (σ2,κ2,δ2) |
|---|---|
| (s-2,1) → (σ3,κ3,δ3) | (s-2,0) → (σ4,κ4,δ4) |
| ... | ... |
| (1,1) → (σ2s-3,κ2s-3,δ2s-3) | (1,0) → (σ2s-2,κ2s-2,δ2s-2) |
| (0,1) → (σ2s-1,κ2s-1,δ2s-1) | (0,0) → (σ2s,κ2s,δ2s) |
La compression des suites binaires par MTS à, disons 4 états, repose sur le principe suivant : on fait tourner toutes les MTS binaires à 4 états en ne retenant que celles qui s'arrêtent en imprimant une suite encore jamais imprimée. Lorsqu'une nouvelle suite apparaît, on symétrise le résultat en lui associant les suites inverse (lue à l'envers), conjuguée (0 et 1 permutés) et inverse de la conjuguée. On range ainsi les suites binaires dans un ordre différent de l'ordre naturel, qu'on pourrait appeler le schéma de compression MTS4 : la complexité algorithmique d'une suite vaut alors le nombre de chiffres significatifs de la représentation binaire de la place qu'elle occupe dans cette nouvelle numérotation et sa profondeur logique vaut (P+1)/2 où P est le nombre (toujours impair) de pas d'évolution de cette MTS minimale.
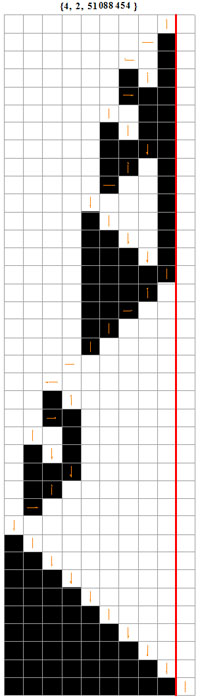
La figure ci-contre détaille l'évolution de la MTS binaire à 4 états portant le numéro 51088454. Elle est la première à imprimer la suite 111111111. La place qu'elle occupe dans l'inventaire des MTS compressantes porte le numéro 83, qui se note 10100112 en binaire. La suite 010011 (le 1 initial n'est jamais significatif chez les entiers binaires positifs) compresse donc la suite 111111111 avec un gain de 3 bits. La complexité algorithmique de la suite 111111111 vaut donc 6 bits et sa profondeur logique vaut la demi hauteur de la table d'évolution de ce programme minimum, soit 19. Mentionnons en passant que la profondeur logique d'une suite, S, de longeur n bits, est toujours supérieure ou égale à n : lorsqu'elle vaut précisément n, le programme minimum n'effectue aucun calcul intelligent : il se contente de construire la suite et de l'imprimer telle quelle en suivant un mouvement de simple aller-retour de la tête. Un tel programme s'appelle une imprimante et on a, en particulier, que le meilleur programme compresseur de toute suite réputée aléatoire ne peut être qu'une imprimante.
Nous sommes à présent en mesure de construire la table des compressions sémantiques des suites par MTS à 4 états. Tous les calculs sont présentés en annexe (Notebook Mathematica). On considère l'évolution des 4294967296 MTS à 4 états (numérotées de 0 à 4294967295) et on note la suite imprimée par la première machine qui s'arrête. C'est la MTS 1 (la MTS 0 diverge vers moins l'infini) : elle imprime la suite 0, à laquelle on attribue le numéro 2 (On convient d'attribuer le n°1 à la suite vide, c'est un détail sans importance). Sa conjuguée, 1, porte donc le n° 3. La MTS suivante qui s'arrête en imprimant autre chose que 0 et 1, déjà comptabilisés, est la MT 278; elle imprime 00 à laquelle on attribue le n° 4. Sa conjuguée, 11, porte donc le n° 5. Poursuivant l'investigation, on trouve que la MT 310 s'arrête en imprimant la suite, 01; on lui attribue le n° 6 donc le n°7 à son inverse (ou sa conjuguée) 10. Plus loin, on trouve, en 38ème position, la MTS 1483700 qui imprime 110101 : celle-ci porte donc le n° 38 d'où 101011 porte le n° 39, 001010 le n° 40 et 010100 le n° 41 (l'ordre n'a pas vraiment d'importance dans cette classe d'équivalence et d'ailleurs le programme Mathematica, fourni en annexe, les classe plutôt dans l'ordre lexicographique).
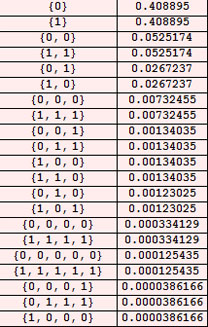
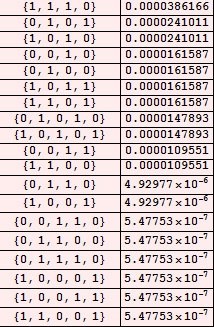
Les calculs menés dans le cas, s=4, répertorient 588 MTS intéressantes, numérotées de 2 à 589. Voici, pour commencer, le tableau du nombre des suites de longueur 1 à 18, imprimées par les MTS à 4 états :
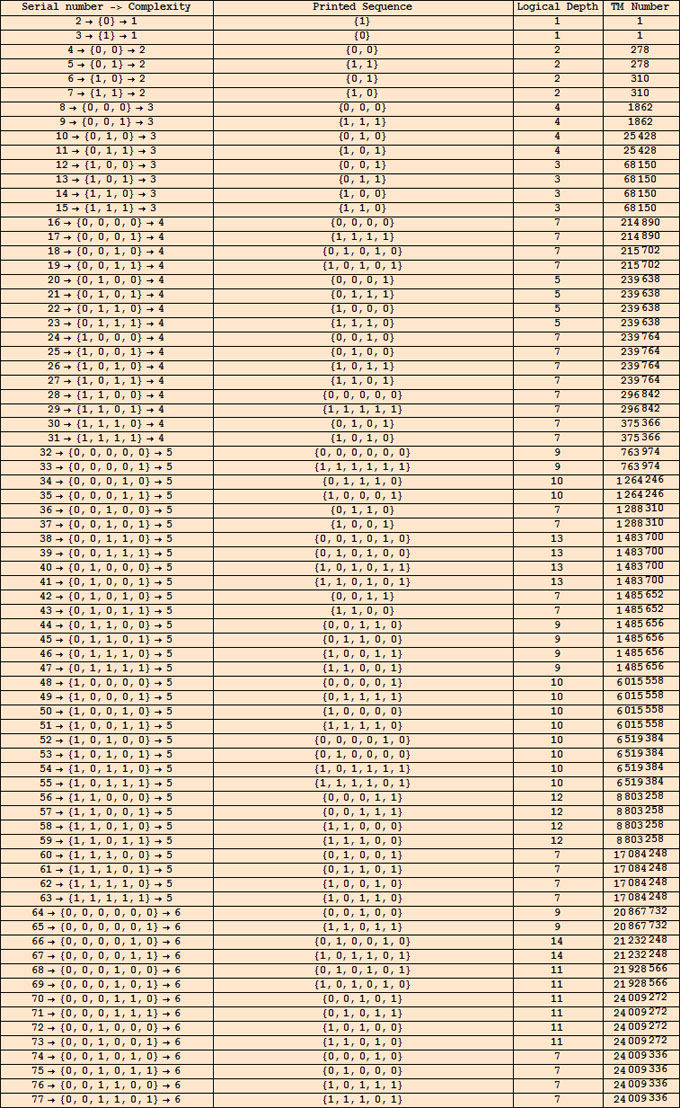
On constate que toutes les suites de longueur inférieure ou égale à 7 sont imprimées dans un ordre à peine bouleversé : seules quelques suites particulièrement régulières viennent s'intercaler entre des suites plus courtes et plus irrégulières.
Si l'on se concentre sur les premières suites imprimées, on constate que les suites de longueurs 1, 2 et 3 bits ne sont ni compressées ni dilatées : elles exigent toujours 1, 2 et 3 bits respectivement. Au sens de Kolmogorov elles peuvent être considérées comme aléatoires ce qui n'a rien de choquant puisqu'on s'attend effectivement à ce qu'un tirage à pile ou face les fasse apparaître fréquemment.
Les choses changent à partir des (16) suites de longueur 4 : 12 d'entre elles exigent encore 4 bits mais 0110, 1001, 0011 et 1100 en exigent 5. Cette dilatation de 1 bit est compensée par la compression de 1 bit de quatre suites de longueurs 5 (01010, 10101, 00000 et 11111). Sans surprise, ce sont des suites particulièrement régulières qui ont été compressées.
Ce phénomène s'amplifie lorsqu'on considère les suites plus longues.
Voici la fin de ce tableau où des suites régulières longues s'intercalent parmi des suites irrégulières plus courtes :
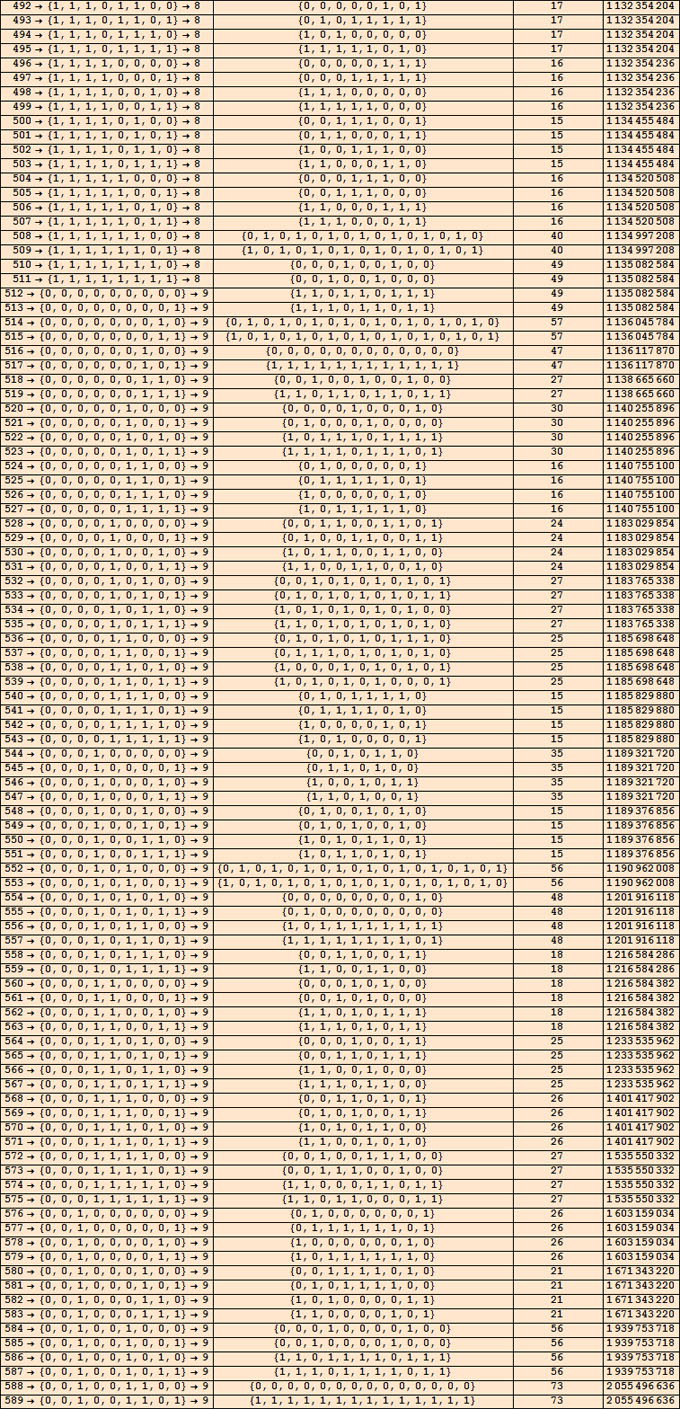
Cette compression par MTS à 4 états n'est qu'une étape d'un processus plus général qui, en théorie, doit être étendu à un nombre croissant d'états. On verrait alors progressivement apparaître les suites actuellement absente de l'inventaire. Une double difficulté surgit à ce stade :
- le temps de calcul explose rapidement, non seulement parce que le nombre des MTS croît rapidement (Il existe (4s)2s MTS binaires à s états, soit respectivement, 4096 (s = 2), 2985984 (s = 3), 4294967296 (s = 4), 10240000000000 (s = 5), ... )
- et surtout, dès que s=5, certaines machines tournent sans faire mine de s'arrêter ni de boucler. On sait que tôt ou tard, on se heurtera au problème générique de l'indécidabilité de l'arrêt des MTS et à sa conséquence naturelle, la non calculabilité de la complexité algorithmique des suites. Nul ne sait à ce jour si les MTS à 5 états sont effectivement concernées par ce problème. Les seuls résultats acquis sont les suivants : les MTS à 2 états (resp. 3 et 4 états) qui s'arrêtent évoluent au maximum pendant 7 pas (resp. 25 et 145 pas) et elles ne produisent aucune suite plus longue que 3 bits (resp. 6 et 18 bits). Lorsqu'on passe à 5 états ces valeurs dépassent certainement 4000 et 47000000 respectivement mais elles ne sont pas connues avec exactitude.