Un problème de trigonométrie “Diophantienne”
![]()
![]()
![]()
![]()
![]()
Liste (volontairement tronquée) des 1980 triplets {u, v, w } lorsque u et v entiers sont en degrés dans les limites autorisées par le problème :
![]()

![]()
![]()
Liste précédente réduite aux 88 triplets {u, v, w } tels que u , v et w sont entiers en degrés :
![]()

![]()
![]()
Dans liste2, u parcourt les valeurs entières, de 1° à 44°; à chaque fois, v vaut 45° ou 90°-2u et w vaut 45°+u. Le triplet, {20, 45, 65}, correspondant au problème d’entrée, est bien présent dans cette liste , en position 39 :
![]()
![]()
Autre façon de formaliser liste2 :
![]()

![]()
| {1,45,46} | {1,88,46} | {2,45,47} | {2,86,47} | {3,45,48} | {3,84,48} | {4,45,49} | {4,82,49} |
| {5,45,50} | {5,80,50} | {6,45,51} | {6,78,51} | {7,45,52} | {7,76,52} | {8,45,53} | {8,74,53} |
| {9,45,54} | {9,72,54} | {10,45,55} | {10,70,55} | {11,45,56} | {11,68,56} | {12,45,57} | {12,66,57} |
| {13,45,58} | {13,64,58} | {14,45,59} | {14,62,59} | {15,45,60} | {15,60,60} | {16,45,61} | {16,58,61} |
| {17,45,62} | {17,56,62} | {18,45,63} | {18,54,63} | {19,45,64} | {19,52,64} | {20,45,65} | {20,50,65} |
| {21,45,66} | {21,48,66} | {22,45,67} | {22,46,67} | {23,45,68} | {23,44,68} | {24,45,69} | {24,42,69} |
| {25,45,70} | {25,40,70} | {26,45,71} | {26,38,71} | {27,45,72} | {27,36,72} | {28,45,73} | {28,34,73} |
| {29,45,74} | {29,32,74} | {30,45,75} | {30,30,75} | {31,45,76} | {31,28,76} | {32,45,77} | {32,26,77} |
| {33,45,78} | {33,24,78} | {34,45,79} | {34,22,79} | {35,45,80} | {35,20,80} | {36,45,81} | {36,18,81} |
| {37,45,82} | {37,16,82} | {38,45,83} | {38,14,83} | {39,45,84} | {39,12,84} | {40,45,85} | {40,10,85} |
| {41,45,86} | {41,8,86} | {42,45,87} | {42,6,87} | {43,45,88} | {43,4,88} | {44,45,89} | {44,2,89} |
Si on se donne les valeurs (entières) de u et w, au lieu de celles de u et v, on observe que deux possibilités existent systématiquement pour v, par exemple si u = 20° et w = 65°, v peut valoir 45° ou 50 °. Les 88 (= 2x44) cas sont réunis dans le montage animé suivant où u est marqué en rouge, v en bleu (deux fois) et w en vert :

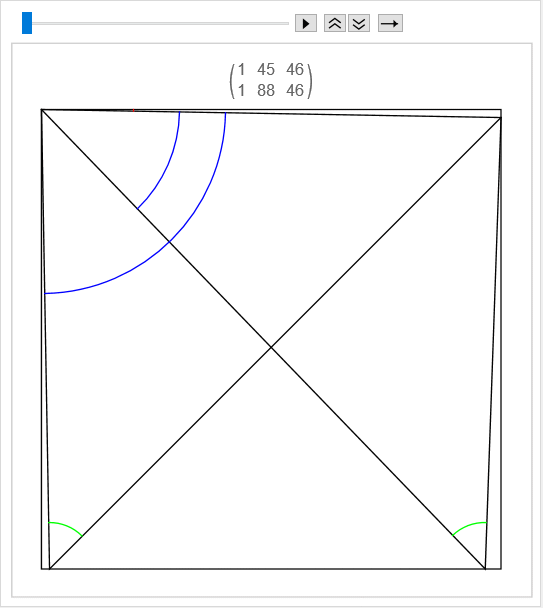
![]()
![]()
L’inventaire, liste3, des solutions entières répond au critère suivant : w = 45°+u. Si on le reporte dans la condition trigonométrique établie dans le texte source, celle-ci se se réduit à l’annulation de l’expression simplifiée suivante :
![]()
![]()
On voit qu’elle donne naissance à deux familles de solutions : cos(2u+v) = 0 → v = 90°-2u et cos(v) = sin(v) → v = 45°. L’inventaire numérique complet des solutions indique que ce sont les seules combinaisons d’angles entiers en degrés.