Faits divers
La Musique parmi les arts (I) :
Peinture et Musique, deux arts disjoints
Sommaire
[ afficher ]- Son et lumière
- Intensité du signal sonore ou visuel
- Fréquence du signal sonore ou visuel
- Peinture continue, composition discrète
- L'espace pictural
- L'espace sonore
- Discrétisation des fréquences
- Discrétisation des durées
- Discrétisation des intensités
- Le phénomène de battement
- Perceptions spatio-temporelles
- La peinture, un art immédiat et fragile
- La musique, un art différé et robuste
- Question de style
- Le rôle du temps
- Synthèse des couleurs et des sons
Peinture et Musique sont, à bien des égards, des arts éloignés l'un de l'autre et cela commence dès l'écolage des artistes impliqués : alors qu'il est parfaitement possible de devenir un peintre de talent sans avoir suivi une formation théorique accaparante au-delà de l'assimilation des règles de base (Lois de la perspective, association des couleurs, maîtrise des clairs-obscurs, ..., en fonction de l'école fréquentée), c'est radicalement impossible en musique où des études longues et sérieuses s'imposent, amorcées si possible dès le plus jeune âge. Certes le talent et l'inspiration sont nécessaires dans les deux cas mais la musique y ajoute un élément savant à tel point qu'en forçant à peine, on pourrait parler d'un art pictural et d'une science musicale. Cette chronique s'intéresse aux éléments qui différencient ces deux arts majeurs.
Son et lumière
Les organes responsables de la vision et de l'audition mettent en jeu des mécanismes physi(ologi)ques complexes qu'il n'est pas question de détailler ici. Nous nous contentons de rappeler les bases essentielles à la compréhension du sujet.
La vue et l'ouïe reposent l'une et l'autre sur l'effet physiologique produit par une onde physique. Toutefois les ondes impliquées sont de natures très différentes :
- Les ondes sonores sont dites matérielles car elles ont besoin d'un support élastique (généralement l'air) pour se propager. Leur détection s'effectue au niveau du tympan de l'oreille externe qui entre en vibration sous l'effet des variations de pression induites, Δp=p-patm, calculées par rapport à la pression atmosphérique régnante (Pour quelques détails, cf, par exemple, Acoustiques musicales).
- Les ondes lumineuses, porteuses de photons, sont de nature électromagnétique et elles se propagent indifféremment dans le vide ou dans la matière transparente (donc aussi dans l'air). La détection des photons s'effectue au niveau de la rétine, composée de ±6 millions de cônes (pour les visions diurne et colorée) et de ±120 millions de bâtonnets (pour les visions nocturne et en noir et blanc).
Dans les deux cas, l'organe qui détecte l'onde transcode les stimuli reçus en signaux électrochimiques envoyés vers des zones spécifiques du cerveau afin qu'ils y soient décodés et interprétés. Deux paramètres importants interviennent à ce stade : l'intensité du signal perçu et sa fréquence (qui précise la couleur de la lumière ou la hauteur du son).
Note. Un troisième paramètre, accessoire en ce qui nous concerne ici, est la vitesse de propagation de ces deux ondes. Dans les conditions usuelles, la lumière se déplace à la vitesse colossale de 300 000 km/s, autant dire instantanément à notre échelle. Il n'existe donc aucun décalage temporel appréciable entre les lumières qui nous parviennent des divers points d'un objet. Il n'en va pas de même en acoustique car l'onde sonore se propage près d'un million de fois plus lentement (340 m/s). Cette fois, un décalage temporel est éventuellement perceptible qui peut poser problème aux ingénieurs responsables de l'acoustique des (grandes) salles.
Intensité du signal sonore ou visuel
L'être humain est capable de détecter des signaux sonores et/ou visuels de très faibles intensités. A l'opposé, il doit se protéger contre les intensités excessives sous peine de dommages irréversibles, au pire en se bouchant les oreilles ou en fermant les yeux. Dans le monde qui nous entoure, ces intensités peuvent varier considérablement :
- En astronomie, le seuil de détection visuel est à peu de chose près atteint lorsqu'on observe la planète Uranus dans un ciel limpide - une denrée devenue rare ! -, ce qui correspond au seuil d'activation de quelques molécules de rhodopsine. En comparaison, l'éclat du soleil est au moins 1032 plus intense ! Bien sûr, il n'est pas question de regarder le soleil en face, la limite tolérée par l'oeil se situant environ 10 ordres décimaux au-dessus du seuil (Rapport 1010).
- La situation de l'oreille est légèrement plus favorable. Entre 1000 et 1500 Hz, la puissance surfacique minimale détectée par un tympan normal vaut de l'ordre de, Imin = 10-12 W/m2, tandis que la valeur maximale tolérée avant la rupture est voisine de, Imax = 1 W/m2. La plage audible en sécurité couvre donc 12 ordres décimaux (Rapport 1012). A basse ou haute fréquences, le seuil est plus élevé et ce rapport diminue légèrement.
Dans tous les cas, il est inenvisageable que le tympan ou les cônes rétiniens relayent linéairement des intensités aussi différentes vers le cerveau. La Nature a de fait prévu que la transduction électrochimique des signaux perçus s'opère selon une loi empirique approximativement logarithmique, (dite) de type "Weber-Feschner" : lorsque l'intensité du stimulus croît selon une progression géométrique, le signal électrochimique ne croît (en gros) que selon une progression arithmétique.
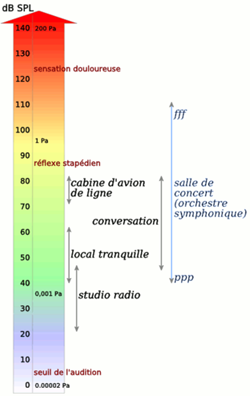
En acoustique, la loi, dB = 10 Log10(I/Imin), définit une échelle logarithmique possible, dite des décibels. Entre 1000 et 1500 Hz, la plage audible en sécurité (par un humain normal) varie entre, dB = 0 et 120 décibels, lorsque I passe de Imin à Imax. Notez l'usage purement conventionnel de la base 10 pour le logarithme et ne vous laissez pas distraire par le facteur 10 multiplicatif qui n'existerait pas si on mesurait les intensités relatives en bels (mais tel n'est pas l'usage).
Si l'on préfère parler en terme de (variations de) pressions exercées sur le tympan, la formule précédente devient, dB = 10 Log10(Δp/Δpmin)2 = 20 Log10(Δp/Δpmin), où le seuil détectable de variation de pression est de l'ordre de, Δpmin = 2 10-5 Pa(scal), soit deux dix milliardièmes de pression atmosphérique. Cette formule, inversée sous la forme, Δp = 2 10(dB/20-5), nous apprend qu'un orchestre symphonique jouant pianissimo (dB ≈ 40 décibels) ou fortissimo (dB ≈ 110 décibels) crée des variations de pressions respectivement de l'ordre de, Δp = 0.002 Pa ou Δp = 6.3 Pa, dans les deux cas des valeurs petites comparées à la pression atmosphérique normale, patm = 101300 Pa (Toutefois, vers 120 décibels, Δp approche 20 Pa, valeur qui signe le seuil de la douleur).
Une loi logarithmique analogue peut être définie à propos des intensités lumineuses mais seuls les astronomes s'en servent pour comparer les magnitudes apparentes des objets célestes. Ils la notent habituellement, m = -2.5 Log10(E/EVega), où l'éclairement de l'étoile Véga sert de référence à la magnitude zéro (Dans cette échelle bizarrement orientée à l'envers, à cause du signe moins dans la formule, Uranus est à la magnitude 5.3, le seuil de détection humaine est proche de 6 et, à l'opposé, le soleil est à -26.7). Cette notion de magnitude n'est d'aucune utilité dans la vie courante (par exemple dans un musée) car les éclairements y demeurent relativement constants.
Le peintre agrée le paramètre "intensité" comme il vient lorsqu'il choisit ses couleurs : il sait que ce que le spectateur verra ne sera jamais que le résultat de la réflexion spontanée de la lumière ambiante sur la toile présumée éclairée idéalement; c'est à prendre ou à laisser. Par contre, le musicien doit gérer l'intensité des sons qu'il veut (faire) entendre en les notant sur une partition.
Fréquence du signal sonore ou visuel
Les plages fréquentielles audibles et visibles (par l'être humain) présentent des différences considérables qui s'avèrent essentielles pour la suite :
- En optique, les fréquences visibles se situent approximativement, du rouge au violet, dans l'intervalle [400, 750] THz (1 THz = 1012 Hz), soit un ambitus, 750/400 = 1.875, inférieur à 2 donc ne couvrant même pas une octave. Si l'on superposait plusieurs ondes lumineuses sinusoïdales de fréquences, k f (k≥1, entier, et f ∈ [400, 750] THz), le résultat serait une onde périodique non sinusoïdale de fréquence, f, dont l'oeil ne percevrait que la composante fondamentale, les autres se situant dans l'ultra-violet. Nous ne saurons donc jamais comment notre appareil visuel percevrait, s'il en était capable, une lumière de fréquence 800 THz, située à l'octave du rouge extrême. L'oeil (humain) n'étant pas sensible au phénomène d'octave, les nuances de couleurs perçues correspondent donc uniquement aux (mélanges des) fréquences fondamentales des ondes réfléchies par la surface regardée.
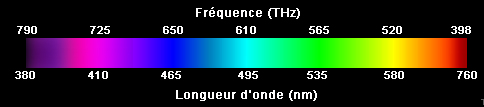
Le spectre visible (D'après Luxorion)
Note. Les physiciens préfèrent mentionner les longueurs d'onde associées, λ, reliées aux fréquences, f, par la relation, f = c/λ, où c = 299792458 m/s désigne la vitesse de la lumière dans le vide. - En acoustique, la plage des fréquences audibles s'étend sur un intervalle beaucoup plus large, [16, 16000] Hz, couvrant approximativement 10 octaves (1000 ≈ 210). Lorsqu'on active, dans l'ordre des fréquences croissantes (de do0 à si9), les touches d'un clavier étendu (d'orgue, par exemple) accordé au tempérament égal, on passe progressivement de la fréquence 16.35 Hz à 15804.3 Hz, selon une progression géométrique de raison 21/12 ≈ 1.05946 et pourtant la sensation ressentie semble parfaitement linéaire . Tout se passe comme si l'échelle des fréquences sonores était perçue selon une loi logarithmique (cette fois mathématiquement) exacte. Dans cette échelle devenue linéaire par construction, la position de n'importe quel son de fréquence f est déterminée par l'intervalle qui le sépare du do0 de départ, Int = 1200 ℓg(f/f0) (mesuré en cents, où ℓg est le logarithme en base 2 et où le facteur 1200 n'est présent que pour la commodité des unités). L'intervalle d'octave vaut alors précisément 1200 cents et, à condition de le diviser en 12 parties égales (ce qui est le cas en tempérament égal), l'intervalle séparant deux notes successives du clavier vaut 100 cents soit un demi-ton tempéré (Cf, par exemple, Gammes et Tempéraments).
Le peintre ne choisit pas directement ses couleurs, il sélectionne des pigments et il s'accommode des couleurs que la toile renverra naturellement vers l'observateur lorsqu'elle sera éclairée. La position du musicien est nettement moins confortable pour deux raisons au moins : primo, le spectre fréquentiel sonore est 500 fois plus étendu que son homologue optique et secundo, le rapport entre les fréquences médianes des deux spectres est colossal, de l'ordre de 1012 (mille milliards !). Les sections suivantes examinent ces différences et en tirent les conclusions qui s'imposent aux (infortunés) musiciens priés d'étudier une théorie musicale astreignante.
L'oreille absolue ?
Tout observateur expérimenté est capable d'ordonner de tête un ensemble de signaux monofréquentiels, visuels ou sonores, dans l'ordre croissant ou décroissant des fréquences. Par contre, il ne peut les quantifier avec précision. Ce n'est guère surprenant : la fréquence d'une onde peut prendre une infinité continue de valeurs dans l'intervalle détectable, qu'il est impossible d'évaluer sous la forme d'un nombre réel comportant une infinité de chiffres décimaux; même une fraction approchée est hors de portée.
L'expérience optique suivante illustre cette impossibilité : si plusieurs observateurs observent la lumière émise par une lampe à vapeur de sodium, tous seront d'accord pour la qualifier de jaune-orange donc d'en situer la fréquence aux environs de 500 THz (Cf l'échelle ci-avant). Aucun ne sera cependant en mesure de préciser qu'elle vaut précisément 508.300 THz et encore moins que deux fréquences extrêmement voisines, 508.127 et 508.474 THz, sont en fait simultanément présentes, bien trop proches pour être distinguées à l'oeil nu. Note. Les longueurs d'onde associées à ce doublet, λ = 589.995 et 589.5924 nm, ne peuvent être séparées que par un spectromètre de laboratoire. Celui-ci révèle d'ailleurs l'existence d'autres longueurs d'onde, par exemple, 568.8 et 615.4 nm, respectivement vertes et marrons, mais leurs intensités sont tellement faibles qu'on ne voit, à l'oeil nu, que la couleur orange dominante.
La même expérience peut être faite en acoustique : un musicien qui entend un son périodique émis par un instrument désaccordé peut, dans le meilleur des cas, situer sa fréquence dans l'échelle des fréquences audibles mais en aucun cas il n'est en mesure de le faire avec précision.
A ce stade préliminaire, une conclusion semble s'imposer : ni l'oeil absolu ni l'oreille absolue n'existent. Certes l'observateur peut estimer que tel objet est "bleu" ou que tel son s'apparente à un "la440" mais le fait qu'il existe à proximité une infinité non dénombrable de nuances empêche de préciser davantage.
Pourtant les musiciens affirment que l'oreille absolue existe et qu'éventuellement ils la possèdent. Il faut comprendre que l'oreille de ces privilégiés n'identifie pas un son périodique quelconque mais une note à condition que la fréquence de celle-ci fasse partie de l'échelle sonore discrète qu'ils ont l'habitude de pratiquer, par exemple l'échelle tempérée. Si on leur soumet un son qui ne correspond à aucune "note-barreau" de cette échelle, ils ne peuvent qu'hésiter entre celles qui l'encadrent.
Peinture continue, composition discrète
La pixellisation de l'espace sonore est au coeur du problème étudié :
- Le peintre travaille en temps réel une toile qui se révèle au fur et à mesure qu'elle se remplit. Il utilise les couleurs avec tous les dégradés imaginables au sein de l'octave visible, veillant seulement a éviter les associations malheureuses. Dans tous les cas, il travaille dans un espace pictural continu.
- Le musicien compose en temps différé : l'oeuvre ne se révélera (au public) que lorsqu'elle sera jouée par un ou plusieurs interprètes. Pour que cela soit possible, il faut qu'une partition soit notée dans un langage susceptible d'être compris par les deux parties et cet intermédiaire exige de travailler dans le cadre d'un espace sonore discret.
L'espace pictural

L'invention de la photographie a un temps semé le trouble parmi les peintres de la fin du 19ème siècle. Cette innovation leur a fait craindre un (court) instant que leur art devienne caduque, supplanté par un mode de représentation absolument fidèle à l'original. Les réactions n'ont heureusement pas tardé : l'impressionnisme de Claude Monnet a trouvé une première parade en privilégiant une restitution hors de portée d'une photographie (trop) occupée à saisir la réalité objective des choses. Tous les courants picturaux qui ont suivi (cubisme, surréalisme, abstraction, etc), ont de fait consacré la victoire de l'imagination sur la reproduction à l'identique. C'est tellement vrai que passé le premier émerveillement causé par la représentation fidèle, le photographe s'est ménagé la possibilité d'imiter le peintre en floutant artistiquement ses clichés.
L'impressionnisme a grandement contribué à révéler un critère fondamental d'appréciation de l'oeuvre d'art : il est essentiel que celle-ci évite d'imposer un point de vue d'appréciation, fût-il suggéré par l'auteur. Elle doit, au contraire, laisser libre cours à l'imagination du spectateur afin qu'il effectue sa part du travail et tant pis si elle se fait dans une direction que l'artiste n'a pas prévue car, dans tous les cas, une fois produite, l'oeuvre ne lui appartient plus. L'expérience montre qu'une oeuvre qui tarde à révéler ses secrets est plus sûrement promise à la postérité, à l'abri du redoutable phénomène de mode.

En temps ordinaires, le tableau représentant la Laitière de Vermeer de Delft est exposé au Rijksmuseum d'Amsterdam. L'image proposée ci-dessus (à gauche !) n'en est qu'une représentation photographique. Apparemment fidèle à l'original, elle repose pourtant sur une discrétisation dont le principe apparaît clairement lorsqu'on dilate le maillage de sa trame. Même lorsque l'image semble nette, elle ne l'est qu'apparemment, abusant simplement le pouvoir limité de résolution de notre oeil. Ce mode de représentation partitionne uniformément l'image en un nombre fixé de pixels quels qu'en soient les détails : sans y prendre garde, à la limite, une image toute blanche (non compressée) serait encore consciencieusement découpée en autant de pixels identiques, occupant en mémoire le même espace qu'une image complexe (Cf Information, Complexité et Musique).
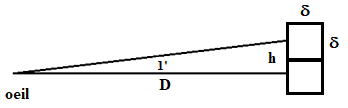
Le pouvoir de résolution de l'œil est proche d'une minute d'arc (1' = 1/60° ≈ 0.00029089 radians), l'autorisant à distinguer un détail mesurant, hcm = 0.0002909 Dcm, sur un objet situé à la distance Dcm (Soit, par exemple, 1 mm à 3 m ou 100 km sur la lune).
La figure ci-avant (pas à l'échelle !) décrit la situation au seuil : deux pixels carrés contigus, mesurant δxδ (cm), sont distants (de centre à centre) de h = δ. On a donc, au seuil, δcm = 0.0002909 Dcm, d'où un nombre de "pixels par cm" valant ppcm = 1/δcm = 3437.73/Dcm. Les anglo-saxons étant passés par là, il est d'usage d'exprimer cette norme en "pixels par pouce" (dpi = dots per inch, 1 inch = 2.54 cm) soit, dpi = 8732/Dcm. Pour un objet situé à 30 cm de l'observateur, la norme optimale au seuil, vaut donc 290 dpi (300 dpi est de fait une valeur courante). Note. Les moniteurs domestiques ne s'approchent guère de cette valeur, ce serait un luxe inutile. Ceux, courants, de 24 pouces (48.8 x 36.6 cm) et proposant 1950 x 1463 pixels épousent la norme 102 dpi.
On peut estimer sur ces bases la quantité de mémoire nécessaire au stockage d'une image non compressée, encore faut-il prévoir le codage de la couleur pour chaque pixel. Celui-ci repose sur l'adoption d'un code RVB, qui répartit linéairement les composantes de rouge, de vert et de bleu, sur une échelle comprise entre 0 et 255, soit 3x8=24 bits/pixel. Note. Ce codage RVB (dit 8 bits) permet d'exprimer 2563 = 16 777 216 nuances distinctes, une valeur inutilement grande puisqu'en pratique, la majorité des humains ne perçoivent pas plus de 300 000 couleurs différentes. Au bilan, le stockage d'une image de dimensions L (cm) x ℓ (cm), destinée à être vue en respectant une norme dpi donnée, occupe en mémoire un espace valant : M = 3 (Lcm dpi/2.54)(ℓcm dpi/2.54) octets. Avec la norme confortable, dpi = 300, une image non compressée mesurant 30 x 45 cm requiert donc un espace mémoire égal à 56497500 octets (56.5 Mo). Evidemment, cette espace-mémoire peut être réduit drastiquement si l'image est compressée, en particulier avec pertes.
En résumé, la pixellisation 2D intéresse le photographe qui souhaite reproduire l'image d'une toile et la stocker dans un espace mémoire sous la forme d'un fichier binaire exploitable. Le degré de précision doit évidemment tenir compte de la distance, Dcm, à laquelle l'observateur est censé se tenir. Cette pixellisation ne concerne pas le peintre qui manie la brosse ou le pinceau de façon continue en s'autorisant tous les dégradés de traits et de couleurs. Le même problème se pose très différemment en musique.
L'espace sonore
En musique, la pixellisation (sonore) s'impose également à l'ingénieur du son responsable de la captation et de la "mise en boîte" d'un concert ou d'un enregistrement de studio : il est bien connu qu'une norme standard d'échantillonnage (wma) requiert 780 Mo pour stocker 80 minutes de musique en qualité CD.
Mais, contrairement à ce qui se passe en peinture, cette pixellisation s'impose également au compositeur car l'oeuvre pensée doit être notée sur partition afin d'être jouée. Or cela passe par l'adoption d'un langage, en particulier d'un alphabet raisonnablement court capable de coder les paramètres d'intensité, de fréquence et de durée des notes et, pour des raisons de décodabilité, cela impose que ces paramètres soient discrétisés. La question à régler en priorité consiste donc à déterminer des valeurs acceptables pour les pixels de chaque espèce.
Alors que l'espace pictural est pixellisé linéairement selon une progression arithmétique, autrement dit proportionnellement aux dimensions physiques de la toile, l'espace sonore doit être pixellisé logarithmiquement, selon un ensemble de (trois) progressions géométriques. C'est la conséquence de l'énorme étendue des plages de fréquences, d'intensités et de durées.
Discrétisation des fréquences
Pixelliser l'espace des fréquences sonores revient à construire une échelle discrète définissant les notes pouvant figurer sur la partition. On serait tenté de penser que la dimension du pixel fréquentiel idéal devrait coïncider avec le pouvoir de résolution (fréquentiel) de l'oreille mais ce n'est pas le cas. Ceci vaut quelques explications.
Bien que le spectre audible, f ∈ [16, 16000] Hz, s'étende sur 10 octaves, celui qui est généralement utile au musicien est plus étroit, réduit, par exemple, à l'intervalle, f ∈ [27.5, 4186] Hz (7.25 octaves), effectivement couvert par le piano de concert moderne. Se souvenant que l'intervalle d'octave séparant deux sons de fréquences, f1 et f2 = 2f1, vaut 1200 cents, la question qui se pose est de savoir en combien d'intervalles élémentaires (pixels) il convient de le partitionner. Il se fait que l'oreille humaine, même exercée, est incapable de distinguer deux sons distants de moins de 5 cents (Cette valeur pouvant varier légèrement avec la fréquence considérée). On en conclut que 5 cents (1/40 ton) représentent la dimension du pixel fréquentiel en-dessous de laquelle il est inutile de descendre. En fait, cette valeur est trop petite pour plusieurs raisons : 1) notre oreille est mal à l'aise avec les micro-intervalles; 2) pixelliser les fréquences de 5 en 5 cents entraînerait de construire une gamme ingérable comportant 240 (= 1200/5) notes par octave; 3) enfin ce serait ouvrir la porte au redoutable phénomène de battement détaillé à la section suivante. En pratique, un pixel fréquentiel valant 100 cents (1/2 ton) convient à nos oreilles contemporaines, partitionnant l'octave en seulement 12 parties égales (12 demi-tons tempérés). Note. A la Renaissance, l'octave était éventuellement partitionnée en 27 intervalles inégaux (permettant de couvrir 21 tonalités majeures de fab à si#). Une telle échelle n'est jouable qu'avec l'adoption d'un tempérament convenable : reportez-vous aux détails exposés dans la chronique Gammes & Tempéraments et assurez-vous que vous avez compris que la discrétisation grossière proposée par le tempérament égal est une injure à la justesse à laquelle nos oreilles contemporaines, de moins en moins exigeantes il est vrai, se sont accommodées comme elles l'ont fait pour toutes sortes d'autres nuisances acoustiques sur lesquelles nous aurons à revenir dans une prochaine chronique.
Discrétiser l'espace des fréquences, c'est se restreindre à un ensemble fini de notes et s'y tenir. On peut y parvenir d'une infinité de manières mais tout le monde s'accorde à considérer qu'il est naturel de respecter en priorité les intervalles les plus consonants, l'octave (1200 cents, f2/f1=2) et la quinte (701.955 cents, f2/f1=3/2). Il est facile de construire une gamme reposant sur ce seul critère. Certes, ce n'est pas exactement celle que les musiciens pratiquent mais elle ne s'en écarte guère et elle est suffisamment simple à mettre en oeuvre pour que l'on comprenne le principe général de la construction d'une gamme. On l'applique ci-après à l'intervalle, f ∈ [27.5, 4186] Hz, couvert par le piano moderne. Partant d'une note initiale médiane, ni trop grave ni trop aigue, par exemple le "la-440 Hz", on étend la gamme en ajoutant à ce "la" les notes situées à un nombre entier d'octaves et/ou de quintes (ascendantes ou descendantes). Cela revient à considérer toutes les notes de fréquences 2k 440 et (3/2)k 440 Hz, où k est un entier, positif, négatif ou nul, tel que les fréquences calculées ne sortent pas de l'intervalle imposé. Les calculs sont élémentaires et on trouve une gamme ne comportant que 19 notes de fréquences, 27.5, 38.6283, 55, 57.9424, 86.9136, 110, 130.37, 195.556, 220, 293.333, 440, 660, 880, 990, 1485, 1760, 2227.5, 3341.25 et 3520 Hz, que l'on a reportées sur l'échelle logarithmique ci-dessous. Ne comptant que 2 ou 3 notes par octave, elle est trop rudimentaire et il faut l'étendre.

Les "la" successifs (en rouge) sont espacés de 1200 cents (Une octave)
Une façon naturelle d'y parvenir repose sur la remarque que si, par construction, toutes les octaves et les quintes (ascendantes et descendantes) du "la" initial ont bien été prises en compte, il n'en va pas de même des octaves et/ou des quintes des 19 notes déjà définies. Par exemple, la note située à la quinte montante de 27.5 Hz, de fréquence 3/2 x 27.5 = 41.25 Hz, est clairement absente de la liste. On remédie à cette situation en étendant la construction précédente aux octaves et aux quintes de la deuxième génération : le nombre total des notes passe alors de 19 à 116; c'est plus qu'un clavier usuel moderne (88 notes) mais cela reste raisonnable. La figure ci-dessous indique la position de ces 116 notes sur la même échelle logarithmique. On constate que tout fictif qu'il soit, ce clavier ne s'écarte guère du clavier usuel réglé sur le tempérament égal. C'est particulièrement net si l'on fusionne les notes apparaissant en doublets. On pourrait continuer l'itération et prendre en compte les générations suivantes d'octaves et de quintes mais cela démultiplierait le nombre des notes, qui passerait à 192, 277, 360, etc, pour un bénéfice acoustique négligeable.

Les "la" successifs (en rouge) sont espacés de 1200 cents (Une octave) et les traits inférieurs, espacés de 100 cents, désignent les notes de la gamme tempérée. On observe l'apparition de doublets caractéristiques de la construction pythagoricienne, espacés de P = 23.46 cents, soit un comma pythagoricien.
Le clavier fictif présenté ci-avant serait parfait s'il autorisait la transposition; malheureusement, ce n'est pas rigoureusement le cas. La gamme réellement utilisée à partir du 19ème siècle est plus simple : elle se contente de discrétiser l'espace des fréquences à pas constant de 100 cents, définissant 12 intervalles égaux par octave (Tempérament égal); certes elle est moins juste mais elle est parfaitement transposable et c'est ce point qui a décidé les musiciens à l'adopter.
La pixellisation par demi tons (100 cents) suffit à nos oreilles occidentales qui peinent déjà à s'habituer aux quarts de tons (50 cents). Les traditions orientales sont moins frileuses, qui n'hésitent pas à explorer les intervalles courts mais c'est au prix de renoncer à la polyphonie qui se heurterait au phénomène de battement (Cf infra).
Note. Il est possible de se faire une idée de ce que représenterait un clavier de piano qui partagerait l'octave en 100 parties égales (notes distantes de 12 cents) : Hidekazu Wakabayashi a réaccordé les 88 touches de son piano domestique en suivant cet accordage bizarre. Evidemment le clavier complet ne couvre même pas une octave (puisqu'il faudrait 100 notes) mais il permet quand même de jouer des mélodies simples .
Discrétisation des durées
Le temps ne compte pas en peinture mais il joue un rôle essentiel en musique, en particulier au niveau de la gestion des durées donc du rythme.
L'oreille ne distingue pas deux sons produits à des intervalles de temps inférieurs à un seuil que le test de Leipp situe entre 25 et 50 ms, la valeur exacte pouvant varier selon les individus (Emile Leipp (1913-1986), actif au CNRS, fut un des pères de l'acoustique musicale, en particulier physiologique). C'est la raison pour laquelle on ne considère généralement pas des notes plus brèves que la quadruple croche qui, dans un tempo, rapide mais standard (allegretto) de 120 noires à la minute (= 2 noires à la seconde), durerait 1/32 ≈ 31 ms.
La théorie en usage devant assurer la synchronisation des interprètes, elle restreint sévèrement l'éventail des durées des notes en définissant, dans l'ordre (des durées) décroissant(es) : la ronde (𝅝), la blanche (𝅗𝅥), la noire (𝅘𝅥), la croche (𝅘𝅥𝅮), la double croche (𝅘𝅥𝅯), la triple croche (𝅘𝅥𝅰) et la quadruple croche (𝅘𝅥𝅱), chaque type étant de durée moitié moindre que celui qui le précède dans la liste. Note. Au Moyen-Age, le plain-chant s'éternisait volontiers sur les syllabes d'où il était courant de considérer des notes de durées plus longues que la ronde, telle la carrée (𝅜) valant deux rondes. Curieusement, on l'appelait aussi "brève" parce qu'il existait une "longue" de durée double (voire triple) ! A l'opposé, il arrive que la musique contemporaine ait recours à des quintuples, voire des sextuples croches, cependant cette pratique est exceptionnelle et ce ne sont pas les interprètes qui protesteront.
On voit que cette échelle des durées suit à nouveau une progression géométrique (et non arithmétique) suivant la formule décroissante, durée(𝅝)/2m (m = 0,1,2,...,6). Cette règle semble suggérer qu'il existe à nouveau une loi de type logarithmique pour la perception des durées. Elle n'a cependant rien d'absolu, la théorie autorisant, si nécessaire, de diviser la ronde par 3 (triolets), par 5 (quintolets), par 7 (septolets), etc. La raison essentielle du découpage géométrique doit être cherchée ailleurs : il facilite le calcul mental de la durée d'une mesure complète, un point qui est examiné ci-dessous.

Toute partition homogène quant à la gestion du temps (physique) est le plus souvent divisée en mesures de durées égales. Celles-ci sont séparées par des barres verticales et numérotées de 1 à N afin que les interprètes puissent se repérer, à tout instant. Chaque mesure est décomposée en un certain nombre (n = 2, 3, 4, ...) de temps forts et faibles afin d'assurer l'accentuation du discours musical. La répartition des temps au sein de la mesure est indiquée par une fraction du type n/2α, où n est le nombre de temps et 1/2α la durée de chacun en terme de (la durée d'une) ronde. Dans l'exemple ci-contre (Aria initial des Variations Goldberg de Bach), les mesures sont notées à 3/4; elles comportent donc trois temps, chacun d'une durée équivalente à un quart de ronde (soit une noire). Révisez vos fractions en contrôlant que le compte des durées vaut, pour chaque mesure, 3/4 de ronde (ou 3/2 de blanche ou 3 noires, etc). Sachez également qu'une note pointée voit sa durée multipliée par un facteur 3/2 et ne tenez aucun compte des petites notes additionnelles qui ne sont que des ornements. Pour que l'information soit complète, il faut encore préciser la durée de la ronde ou ce qui revient au même de la noire (à condition de diviser par 4), ce qu'on nomme le tempo. Les musiciens ne cultivant pas la simplicité, ils ont choisi de définir ce tempo de façon indirecte, en fixant le nombre de noires à la minute, noté : ♩=η. Par exemple, ♩=120, signifie 2 noires à la seconde soit 0.5 s par noire. A partir de ces données, on calcule sans (trop de) peine la durée d'une mesure soit, (240/η) (n/2α) donc celle d'un morceau homogène complet, comportant N mesures : durée = N(240/η) (n/2α). Par exemple, le Boléro de Ravel comporte 340 mesures à 3/4; si l'on adopte le tempo, ♩=η=72, on trouve que l'oeuvre complète dure, 340 (240/72)(3/4) = 850 s soit 14:10. Note. En fait, Ravel a modifié plusieurs fois le tempo souhaité, entre ♩=64 et ♩=76, sans en imposer aucun, d'où il ne faut pas s'étonner de trouver des enregistrements de durées variables en fonction du choix des chefs, allant de 12:00 (Stokowski, ♩=84) à 18:30 (Freitas Branco, ♩=54). Le Boléro n'a pas été choisi au hasard : de fait, l'oeuvre est d'un seul tenant au plan de la mesure. La plupart des oeuvres ne le sont pas, ce qui exige, pour calculer leur durée totale, d'additionner les durées des sections individuelles.
La théorie évoquée présuppose que les mesures sont de durées égales. On comprend mieux, à présent, pourquoi les durées des notes suivent une progression géométrique : pour comptabiliser les durées au sein d'une mesure, il faut additionner des fractions, ce qui est simple si les dénominateurs sont tous des puissances de 2. Rien n'empêche en théorie de considérer un mètre variable (il était courant à l'époque baroque) mais cela complique la tâche des interprètes (On trouve des tentatives du genre dans l'oeuvre de Boris Blacher).
La mention d'un tempo sur la partition est une invention relativement récente (200 ans tout de même, lorsque l'usage du métronome s'est généralisé). Pendant longtemps, on s'est contenté d'indications qualitatives selon une échelle allant du plus lent au plus rapide : Largo (η < 60), Lento (52 - 68), Adagio (60 - 80), Andante (76 - 100), Moderato (88 - 112), Allegretto (100 - 128), Allegro (112 - 160), Vivace (~ 140), Presto (140 - 200) et Prestissimo (>200). A l'époque de Bach, l'indication pouvait être encore plus vague, voire inexistante comme dans l'Aria ci-avant. Bien qu'il s'agisse d'une Sarabande, lente en principe, il apparaît que les interprètes traitent souvent cette indication avec légèreté voire extravagance, revendiquant leur part de liberté dans l'exécution. Par exemple, au clavecin, l'excellent Jean Rondeau met 270 s pour jouer les 32 mesures à 3/4 de l'aria complète, ce qui correspond à un tempo assez lent, de l'ordre de ♩=η=21. Blandine Verlet se situe dans la norme dans cette première version (170 s pour l'aria complète, soit ♩=η=34) et beaucoup moins dans cette autre nettement plus rapide (145 s pour l'aria complète, soit ♩=η=40). Veuillez noter que les éditeurs ont aussi leur conception de la norme : il tiennent souvent à ce que l'oeuvre complète tienne sur un seul CD, ce que la version Rondeau ne permet pas ! Cela dit, la palme de la lenteur revient incontestablement au pianiste Lang Lang qui étire exagérément l'aria pendant 335 s (♩=η=17) !
Discrétisation des intensités
Un compositeur ne code pas seulement la fréquence et la durée des notes mais aussi leur intensité. Pour ce faire, il pourrait recourir à l'échelle des décibels mais il ne le fait pas, se contentant d'indications qualitatives selon une échelle déclinant les nuances, ppp (pianississimo), pp (pianissimo), p (piano), mp (mezzo piano), sotto voce, mf (mezzo forte), f (forte), ff (fortissimo), fff (fortississimo). Cette séquence revient à discrétiser à la (grosse) louche l'échelle des intensités par pas de 6 à 7 décibels. L'imprécision peut surprendre mais elle présente au moins l'avantage de laisser une certaine latitude aux interprètes qui, de fait, ne s'en privent pas.
Quelques compositeurs ont tenté de marquer les esprits par quelques notations fantaisistes abusant d'une accumulation de p ou de f : ainsi György Ligeti a clos son Etude n°9, pour piano, sur un présumé inaudible pppppppp ou encore, il a introduit une transition tonitruante de ffffff à ffffffff (!) dans son Etude n°13. L'écoute confirme s'il en était besoin que ces indications ne correspondent à aucune intensité objective; elles suggèrent simplement aux interprètes de pousser leur jeu dans ses derniers retranchements, ce qu'ils font le plus souvent en prenant les plus grandes libertés.
Le phénomène de battement
Les battements sonores sont indirectement utiles aux musiciens lorsqu'ils accordent leur instrument en opérant les réglages qui les font disparaître. Dans tous les autres cas, ils sont nuisibles car ils sont un obstacle à la justesse musicale. Rappelons les bases physiques du phénomène.
Si l'on superpose deux ondes sonores de mêmes fréquences, on entend sans surprise une onde résultante de même fréquence. Si les fréquences diffèrent nettement, on les entend distinctement. Rien n'est étrange à ce stade. Par contre, si les fréquences sont proches, différant de 5 à 35 Hertz environ, le résultat peut s'avérer gênant : on entend une onde de fréquence intermédiaire (en moyenne arithmétique) dont l'amplitude varie périodiquement à une fréquence, dite de battement, égale à la différence des fréquences superposées. Il en résulte un effet de bourdonnement désagréable.
On sait, depuis les travaux d'Helmholtz (1821-1894), que ces battements sont en partie responsables des dissonances entre les notes mais on sait également, depuis les travaux de Carl Stumpf (1848-1936), que des éléments psychoacoustiques interviennent également. Les musiciens, qui se fient plus volontiers à ce qu'ils entendent qu'à ce que d'autres calculent, ont classé les 13 intervalles simples dans l'ordre suivant, du plus consonant au plus dissonant : unisson (do-do = 0 cent) et octave (do-do suivant = 1200 cents), quinte (do-sol = 700 cents), quarte (do-fa = 500 cents), tierce majeure (do-mi = 400 cents), sixte majeure (do-la = 900 cents), tierce mineure (do-ré# = 300 cents), sixte mineure (do-sol# = 800 cents), septième mineure (do-la# = 1000 cents), seconde majeure (do-ré = 200 cents), triton (do-fa# = 600 cents), septième majeure (do-si = 1100 cents) et seconde mineure (do-do# = 100 cents). Ils ont également noté, primo, qu'à intervalle égal, la consonance se dégrade lorsqu'on descend dans le grave (et inversement s'améliore lorsqu'on monte vers l'aigu) et, secundo, que la dissonance est atténuée si l'intervalle est augmenté d'une octave, telle une quatorzième majeure (do-si suivant = 2300 cents), moins dissonante que la septième correspondante.
On situe mieux la part des battements dans les observations précédentes si l'on affiche le tableau des fréquences des notes appartenant à l'échelle accordée au tempérament égal :
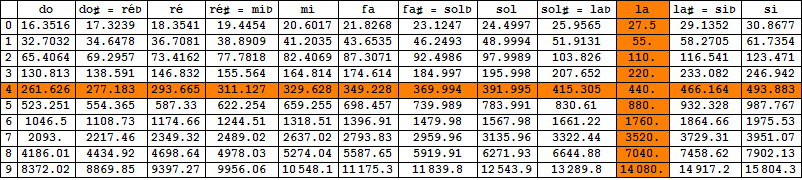
L'octave médiane (surlignée horizontalement) offre un bon point de départ : on constate que les notes do et do# sont distantes de 15.5 Hz et que les notes do et ré sont distantes de 32 Hz, soit des valeurs situées dans la zone de battement. On ne s'étonne donc pas que les intervalles correspondants (seconde mineure et seconde majeure) soient classés comme dissonants. Poursuivant l'exploration, on tombe sur les notes do et ré# distantes de 49.5 Hz, une valeur extérieure à l'intervalle 5-35 Hz. Il ne faudrait pas trop vite en conclure que l'intervalle correspondant (tierce mineure) est consonant car un battement secondaire se produit entre le 6ème harmonique du do et le 5ème harmonique du ré# (6x261.626-5x311.127=14.12 Hz). Le lecteur motivé peut vérifier qu'aucun battement secondaire ne se produit entre les notes do et sol ou do et fa : les intervalles de quinte et de quarte sont justes (Cf l'exposé antérieur, Gammes et Tempéraments).
C'est en partie afin d'éviter les battements sonores qu'une théorie musicale complexe a vu le jour dès la Renaissance. Les musiciens ont compris que le mélange des voix ne pouvait se faire au hasard et qu'il exigeait l'apprentissage d'une science combinatoire musicale. On peut être un peintre amateur de talent, c'est chose impossible en musique sauf à se cantonner dans des musiques rudimentaires ne prenant aucun risque harmonique ou contrapuntique.
Le phénomène de battement ne joue aucun rôle en optique (scintillation) car le phénomène d'octave y est absent et quand bien même il existerait, il serait indétectable car l'ordre de grandeur des fréquences optiques visibles est mille milliards de fois plus élevé que celui des fréquences acoustiques audibles. La rencontre de fréquences voisines est dès lors pratiquement impossible.
Perceptions spatio-temporelles
L'oeil et l'oreille sont incapables de quantifier précisément les paramètres spatio-temporels, laissant par exemple planer un doute sur la dimension d'un objet ou sur la durée d'un son.
- Les Anciens, qui avaient du temps libre, attachaient de l'importance à des détails qui ne nous préoccupent plus guère aujourd'hui. Ils s'intéressaient, en particulier, aux proportions, L(ongueur)/ℓ(argeur), du rectangle idéal pouvant servir de modèle à, par exemple, la façade du Parthénon. Partant de l'idée assez naturelle qu'un rectangle trop plat ou trop carré manquerait d'élégance, ils ont conclu qu'il devait "forcément" exister un "idéal" entre ces extrêmes, peut-être un rapport, L/ℓ = 3/2 ou 4/3, au motif qu'il aurait plu aux pythagoriciens, férus de fractions simples. Cependant ce genre d'argument se heurte au fait que lorsqu'on demande à des observateurs de sélectionner "le rectangle idéal" sur base d'un rapport L/ℓ situé entre des limites raisonnables, disons, 4/3 (= 1.333) et 8/5 (= 1.6), ils échouent à se mettre d'accord. Cela ne surprend guère : notre oeil, si prompt à distinguer des détails infimes ou à percevoir des intensités faibles, n'est pas du tout équipé pour apprécier les proportions d'un rectangle fourni sans autre explication. Il est déjà incapable de décider lequel des rectangles ci-après respecte rigoureusement la proportion 3/2.
L'intuition ne leur ayant été d'aucun secours, les Anciens ont alors opté pour une solution "ésotérique", décrétant arbitrairement que le rapport idéal devait répondre à la proportion peut-être "divine" mais sûrement alambiquée, L/ℓ =(L+ℓ)/L (plus facile à appréhender si on la traduit avec des mots : la longueur est à la largeur ce que le demi-périmètre est à la longueur). Un peu d'algèbre révèle que ce rapport "idéal" vaut, L/ℓ = (1+√5)/2 ≈ 1.618. Il est connu depuis l'Antiquité sous le nom de "Section d'Or" et le Parthénon est censé en offrir une illustration parfaite.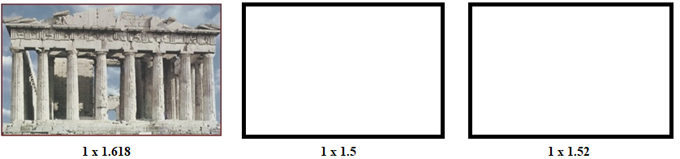
- Vers la même époque, des membres de l'école de Pythagore se sont intéressés à la consonance des sons de fréquences différentes. Procédant expérimentalement à l'aide d'un monocorde, ils ont abouti à la conclusion (cette fois argumentée !) que le critère basé sur les fractions simples tenait la route. De fait, ils ont trouvé que l'oreille est capable de distinguer les cas où deux sons émis simultanément sont dans un rapport fréquentiel égal à 3/2 (quinte exacte) ou seulement proche de cette valeur : il suffit de les jouer simultanément et d'observer que seule la quinte juste est exempte de battement.
Quinte juste (f2/f1 = 1.50) Quinte fausse (f2/f1 = 1.52)
Avatars de l'oeuvre d'art
Les différences observées dans le traitement des paramètres sonores ou lumineux expliquent en quoi le "métier" de peintre diffère de celui de compositeur. Qu'en est-il de l'oeuvre achevée ?
La peinture, un art immédiat et fragile
D'un siècle à l'autre, les peintres n'ont pas été égaux devant le temps de la conception. Jadis, la culture du détail apparentait la peinture à un jeu de patience au point que pour honorer les commandes de plus en plus nombreuses, les artistes en vue confiaient une partie du "travail" à des élèves formés, les rectifiant au besoin. Les choses ont bien changé au vingtième siècle et on a connu des artistes peignant plusieurs toiles par jour !
La peinture est un art immédiat : rien ne s'oppose à ce qu'une oeuvre achevée soit immédiatement exposée. Cette relation de proximité entre le peintre et son public semble attractive mais un problème surgit dès que l'artiste souhaite négocier son oeuvre, il faut bien vivre ! Des intermédiaires intéressés, dans tous les sens du terme, galeristes, agents, marchands et même critiques d'art, entrent alors en scène, conscients des leviers qu'ils détiennent. A terme, la plupart des tableaux de valeur disparaissent dans des collections privées, ne rejoignant éventuellement un musée que beaucoup plus tard, à la faveur d'acquisitions publiques ou de dations. Entre-temps, ils passent discrètement de mains en mains, gagnant en valeur marchande sans autre bénéfice pour leur auteur que de faire monter leur cote, encore faut-il qu'il soit encore en vie pour en profiter ! Sauf acquisition muséale ou rétrospective ponctuelle, tout tableau de valeur est donc rapidement soustrait à l'attention du public et ce n'est pas la pire éventualité car d'autres sorts moins enviables le menacent :
- Un tableau peut disparaître définitivement lors d'un désastre naturel, un tremblement de terre (Naples 1798), un incendie (Alcazar de Madrid en 1734) ou un bombardement (Dresde en 1945), cf cette longue liste.
- Il peut également être volé et jamais retrouvé (Ce site vous rappelle quelques exemples tristement fameux avec une mention spéciale pour la collection du Musée Isabella Stewart Gardner de Boston, qui a "perdu", un matin de 1990, 13 toiles de Maîtres non retrouvées à ce jour). On déplore particulièrement le vol du panneau des Juges intègres de L'Agneau mystique de Jan van Eyck (Gand, 1934) et celui de La Nativité du Caravage (Palerme, 1969).
- Enfin, il peut subir toutes sortes d'avaries, volontaires (actes de vandalisme) ou involontaires (restauration manquée, altération naturelle des couleurs, dégradation liée au temps qui passe). Certaines églises sont même pleines de toiles carbonées dont les couleurs ont tellement souffert qu'aucune restauration n'est raisonnablement envisageable. Il est bien connu que les couleurs d'origine vieillissent plus ou moins bien et que celles utilisées par Jan van Eyck ont nettement mieux résisté que celles expérimentées par Léonard de Vinci. Personne ne sait aujourd'hui ce que deviendront les toiles de Vincent van Gogh dans 500 ans et des travaux de restauration peuvent s'imposer avec pour conséquence de nous éloigner progressivement de l'original. Tout restaurateur agit alors comme un intermédiaire qui interprète plus ou moins fidèlement les directives émanant d'experts. Les restaurations coûtant très cher, elles sont réservées aux oeuvres majeures; quant aux autres, elles sont à terme plus ou moins lointain menacées de disparition.
La peinture connaît le phénomène de la copie, didactique ou frauduleuse. Par didactique, on entend le cas du peintre qui souhaite se faire la main voire proposer à des amateurs des répliques de chefs-d'oeuvre dans le respect de la réglementation en usage (Dimensions altérées, signature dépourvue d'ambiguïté, ...). Aussi parfaite soit-elle, une copie ne possédera jamais une valeur marchande comparable à celle de l'original. A ceux qui s'étonneraient qu'une telle différence puisse exister entre deux objets indiscernables à l'oeil nu, il est d'usage de rappeler que la notion de prise de risque est essentielle dans le domaine de l'Art, où pour paraphraser Paul Gauguin, "Tout ce qui n'est pas révolution est plagiat". De fait, un copiste ne prend aucun risque en copiant un chef-d'oeuvre consacré.
Il est clair que le vol d'un tableau est la conséquence funeste de sa valeur marchande d'où il résulte que le phénomène inverse existe également où des oeuvres apparaissent sur le marché, jamais peintes par l'auteur désigné. Les amateurs d'art ont gardé en mémoire l'exemple rocambolesque du marchand Fernand Legros qui a dévoyé à son profit le talent des peintres faussaires (hongrois) Elemér Albert Hoffmann et (canadien) Réal Lessard.
L'art musical échappe à de telles dérives. Personne n'a jamais copié l'oeuvre musicale d'un Maître, tout au plus l'a-t-il transcrite de sa main, à des fins didactiques. Le "métier" de faussaire musical n'existe donc pas et il vaut la peine de réfléchir aux raisons profondes de cette particularité. Composer une oeuvre importante prend beaucoup de temps à son auteur d'où le catalogue complet excède rarement quelques centaines d'oeuvres, toutes généralement bien documentées dans la littérature. Tout candidat faussaire qui exhiberait une partition de son invention en la faisant passer pour l'oeuvre d'un grand Maître serait immédiatement démasqué. La chronique rapporte néanmoins deux exemples anecdotiques : le célèbre adagio d'Albinoni est un artefact dû au musicologue Remo Giazotto qui a prétendu avoir complété un fragment (jamais retrouvé) d'une Sonate en trio du maître vénitien ! Un autre exemple est dû à Winfried Michel, qui a prétendu avoir mis à jour 6 sonates perdues de Joseph Haydn, parvenant même à abuser le spécialiste Howard Chandler Robbins Landon. Précisons que ces faux en écriture musicale n'ont pas rapporté le moindre kopeck à leur auteur.
La Musique, un art différé et robuste
La Musique est un art différé : pour communiquer avec ses auditeurs potentiels, le compositeur doit impérativement passer par toutes sortes d'intermédiaires (copiste, éditeur, interprète). Toute musique pensée intérieurement avec la vocation de survivre doit être notée dans un langage suffisamment puissant pour (espérer) ne manquer aucune nuance. Une partition n'étant accessible qu'à l'extrême minorité de ceux qui "lisent la musique", un interprète s'avère indispensable, capable de traduire les intentions du compositeur.
Cependant l'existence même d'un interprète est en soi un obstacle à la fidélité de l'oeuvre jouée par rapport à l'oeuvre pensée et, de fait, pour une oeuvre donnée, il n'y a pas deux restitutions sonores identiques. Loin d'être un handicap, cette diversité des interprétations fait partie des richesses de l'art musical : elle explique, en particulier, qu'un auditeur ne se lasse pas de réentendre autrement une oeuvre qui lui tient à coeur. C'est particulièrement le cas des amateurs d'opéra qui sans cela tourneraient le plus souvent en rond dans un répertoire plutôt exigu.
Les catastrophes évoquées à propos des peintures - destructions, pertes, vols, avaries, falsifications - menacent peu la Musique : pour des raisons évidentes, jamais on n'abîmera ou ne perdra le Requiem de Mozart. La seule mésaventure qui puisse affecter une oeuvre musicale est la perte de sa partition autographe qu'on aurait omis de (re)copier. La négligence la plus tragique concerne une bonne partie de l'oeuvre d'Albinoni (dont pas moins de 70 opéras, perdus définitivement !), détruite lors des bombardements de Dresde. D'autres exemples plus déconcertants concernent des oeuvres volontairement détruites par leur auteur, insatisfait ou dépressif (Dukas, Duparc, Sibelius, ...).
Question de style
L'Histoire des Arts divise habituellement l'échelle du temps en périodes créatrices partageant une intention stylistique commune. Sans entrer dans les détails, elles se nomment, Moyen-Age, Renaissance, (Période) Baroque, Classicisme, Romantisme, (Ere) Moderne et (Epoque) Contemporaine. Tous les arts majeurs adhèrent à cette classification à condition d'adapter les dates de début et de fin de chacune des périodes. Ce qui change éventuellement, surtout à partir du 19ème siècle, ce sont les sous-périodes, présentes pour certains arts et absentes pour d'autres. Ces mouvances particulières ont généralement pris naissance dans des cercles littéraires avant de diffuser parmi les peintres et/ou les musiciens toutes les fois que leur art particulier y trouvait un champ d'illustration.
On peut expérimenter la ligne du temps pictural en parcourant n'importe quel musée important dans l'ordre chronologique des salles. On observe que les styles défilent d'abord lentement (Moyen-Age, Renaissance, Baroque, Classicisme, Romantisme) puis de plus en plus rapidement, à partir des années 1870, date à partir de laquelle les historiens ne suivent plus à catégoriser les styles en Académisme, Symbolisme, Impressionnisme, Expressionnisme, Cubisme, Naturalisme, Vérisme, Dadaïsme, Surréalisme, Védutisme, Constructivisme, Suprématisme, Maniérisme, Réalisme, Minimalisme, ..., il y en a pour tous les goûts.
L'Histoire de la Musique suit une échelle temporelle facile à mémoriser à condition d'arrondir (légèrement) les dates. Cette échelle est nettement moins chargée que sa consoeur picturale du fait qu'elle ignore nombre de variantes (postérieures à 1870) qui lui sont étrangères sauf éventuellement à l'opéra (Naturalisme, Vérisme, ...) mais c'est alors le traitement de l'argument théâtral qui est en cause.

Voici quelques exemple d'expressions stylistiques communes à la peinture et à la musique :

- Le Réalisme s'est attaché à mettre en scène la vie, insouciante ou laborieuse, des gens ordinaires. Il l'a montrée telle qu'elle était, sans chercher à l'idéaliser (Giacomo Puccini : La Bohème).
Son prolongement, le Naturalisme y a ajouté des préoccupations sociologiques tendant à démonter les mécanismes capables de maintenir des individus d'extraction présumée modeste dans toutes sortes de précarités (Gustave Charpentier : Louise; Alfred Bruneau : Lazare).

- Le symbolisme peut être vu comme une réaction artistique au naturalisme, jugé terre-à-terre voire misérabiliste. Il s'est décliné en plusieurs tendances selon qu'il a abandonné la réalité morose pour celle du sacré, du rêve éveillé ou de la spiritualité (variante onirique) ou pour celle du chimérisme voire de l'occultisme très à la mode à cette époque (variante ésotérique). Bien que de nombreux musiciens aient adhéré au projet, ils l'ont fait avec des sensibilités différentes en Allemagne (Richard Wagner : Parsifal), en Autriche (Alexander Von Zemlinsky : Symphonie lyrique), en France (Claude Debussy : Pelléas et Mélisande) ou en Russie (Scriabin : Poème de l'Extase).

- La référence à Debussy, au paragraphe précédent, peut surprendre alors que l'artiste est généralement catalogué comme le fondateur du mouvement impressionniste. C'est la conséquence de l'ambiguïté fondamentale qui a marqué sa démarche musicale. Chez Claude Debussy (La Mer), l'impressionnisme a largement été dicté par un besoin de réaction patriotique au wagnérisme ambiant qui le fascinait cependant. Il a été accompagné dans sa démarche par quelques disciples de la première heure (André Caplet, Déodat de Séverac) et ultérieurement par des admirateurs désireux de se rassembler sous une banière prestigieuse (Maurice Ravel, Charles Koechlin, voire Olivier Messiaen, et dans les pays anglo-saxons, Frederic Delius et Charles Tomlinson Griffes).

- L'expressionnisme a été la réponse germanique à l'impressionnisme français, prônant cette fois l'urgence de la sensation émotionnelle. Le projet était sensé en peinture, un art particulièrement apte à capturer les émotions dans leur instantanéité. Il était davantage problématique en musique précisément parce que l'oeuvre musicale s'étale dans le temps. C'est pourtant ce qu'ont tenté de faire quelques musiciens germaniques, inspirés il est vrai par les turbulences d'une Allemagne plongée en plein désarroi d'entre-deux guerres (Arnold Schönberg : Pierrot lunaire). Sans grande surprise, l'expressionnisme musical n'a pas fait fortune en France.
Entre les deux guerres mondiales, la peinture moderne s'est diversifiée au départ de trois tendances dominantes, le surréalisme, le cubisme et l'abstraction.



- La musique a ignoré le surréalisme : n'exprimant aucune idée intellectuelle, elle ne pouvait s'ingénier à la détourner. Par contre, le cubisme et l'abstraction ont été de sa compétence, en illustration de cette formule (un peu) expéditive selon laquelle "La mélodie serait à la musique ce que le dessin est à la peinture".
- Le cubisme n'élimine pas le dessin, il réduit les contours à des formes stylisées quoique parfaitement reconnaissables. L'équivalent musical a donc abandonné la mélodie sinueuse (Richard Strauss : Zueignung) pour lui substituer une variante linéaire accentuée par le déhanchement rythmique (Arthur Lourie : Gigue, Igor Stravinsky : Ragtime). Il a disséminé partout dans le monde, révélant de multiples variantes selon le pays d'accueil : constructivisme russe (Alexander Mossolov : La fonderie d'acier), machinisme américain (George Antheil : Airplane Sonata) ou futurisme italien (Francesco Pratella : Trio à clavier).
- L'abstraction picturale a franchi un pas supplémentaire en éradiquant toute forme de représentation des contours. En musique, cela correspond à la perte des repères tonals tels que codifiés par les tenants de la musique dodécaphonique et surtout de son extension sérielle (Anton Webern : 5 Pièces, opus 10).
Or le grand public se passe plus aisément du dessin que de la mélodie et il ne fait guère de doute que cela a contribué à l'éloigner d'une musique contemporaine phagocitée par les techniques sérielles pendant les décennies 1945-75. Il a dès lors déserté la création musicale qui lui était en principe destinée, omettant majoritairement de revoir son point de vue lorsque s'est opéré un retour progressif vers une nouvelle modalité (Cf Modalité musicale et arithmétique modulaire et Musique 2001 pour une synthèse). Le contraste est frappant avec ce qu'on observe en peinture où aucune rétrospective ne rebute le public cultivé, même si elle rassemble des oeuvres de création récentes.
Le rôle du temps
La gestion du temps musical est une autre source de difficultés pour le public : on peut acquérir une bonne connaissance du "répertoire pictural" dans des délais raisonnables, c'est radicalement impossible en musique qui est par essence un art chronophage.
Une seule audition ne permet généralement pas d'appréhender une oeuvre un peu complexe et si celle-ci est longue, le temps qu'on devra lui consacrer sera considéré comme prohibitif par le plus grand nombre. Découvrir un répertoire musical étendu exige donc d'y passer une partie non négligeable de son temps, ce qui décourage nombre d'amateurs. Si l'on se contente d'une écoute domestique, il est vrai qu'on peut l'interrompre à tout moment mais si on prend le risque de fréquenter les salles de concert, ce qui est quasiment une nécessité si l'on veut progresser, alors le risque est réel de se sentir piégé par une demande intellectuelle qu'on aurait mal estimée.
Synthèse des couleurs et des sons
Au cours des siècles, Peinture et Musique ont acquis leurs titres de noblesse sur base d'une activité mêlant l'artisanat à la technique. Un phénomène nouveau est apparu au 20ème siècle, marginal à ses débuts puis de plus en plus envahissant, celui de l'art de synthèse.
Avec le progrès des sciences appliquées, on a vu apparaître surtout après 1945, des produits de synthèse visuels et sonores apparemment performants, en tous cas façonnables et reproductibles à l'infini. Ils promettaient aux peintres de les affranchir des contraintes liées aux pigments disponibles (Cf les oeuvres récentes du britannique David Hockney, réalisées à partir d'un iPad; illustration ci-après) et aux musiciens de renouveler le cadre acoustique d'un instrumentarium figé par le temps (Principe du synthétiseur).
- Chez l'humain non daltonien, les cônes rétiniens existent en trois variantes dont la bande passante est centrée sur les fréquences Rouge, Verte et Bleue. L'idée a dès lors fait son chemin qu'il devait être possible de reconstituer n'importe quelle nuance de couleur sur base d'une proportion bien calibrée de ces trois teintes de base. C'est en substance ce que fait la synthèse informatique lorsqu'elle recourt à un codage (tri)chromatique précisant les proportions de chacune des couleurs fondamentales (Codage RGB, de l'anglais Red-Green-Blue). Les couleurs de base ont été fixées conventionnellement par une Commission internationale aux longueurs d'onde suivantes : rouge (700,0 nm, 428 THz), vert (546,1 nm, 549 THz) et bleu (435,8 nm, 688 THz). L'informatisation de la méthode requiert de discrétiser chaque composante par exemple sur 8 bits (1 octet), ce qui permet de la faire varier entre 0 et 255 (= de 0 à 100%). Cela suffit amplement puisque cela autorise 2563 = 16 777 216 nuances différentes, alors que l'oeil humain n'en distingue guère plus que 300 000 à 2 000 000, les avis divergent. Les figures ci-dessous présentent une vision (faussement) 3D (simplifiée à 3 bits au lieu de 8) du cube de représentation colorée tel que vu de 8 points de vue différents. Exercez-vous à passer du noir (Toutes les composantes RGB sont nulles) au blanc (Toutes les composantes RGB sont saturées à 1) en transitant par tous les intermédiaires possibles (Par exemple, Jaune = {Rouge=1, Vert=1 et Bleu = 0}).
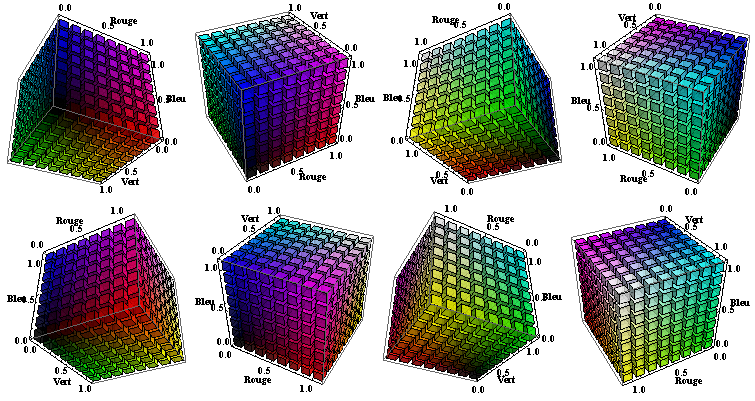
Codage simplifié (sur 3x3x3 bits) d'un espace restreint à (23x23x23=512) couleurs.
Ce qui frappe l'oeil dans ces exemples, c'est le caractère "métallique" des couleurs ainsi restituées. Les utilisateurs de programmes de traitement d'images le savent bien : toute reproduction picturale synthétisée par quelque procédé que ce soit doit être retouchée si elle veut restituer la patine de la toile originale. - Le synthétiseur musical donne, lui aussi, l'illusion qu'il ne connaît aucune limite dans la création de sonorités nouvelles. Les musiciens Ambiant ou New Age (Brian Eno, Vangelis, l'étonnant Harald Weiss et tant d'autres) en ont fait un usage régulier. Même John Adams a eu recours épisodiquement aux possibilités offertes par la "Korg Wavestation" et les "Claviers Yamaha" mis à sa disposition lors de séjours à l'Université de Berkeley (Hoodoo Zephyr, 1992, Part 4 "Tundra" ). Il n'a cependant pas insisté dans cette voie, conscient des limites de l'électronique musicale : si celle-ci est en théorie capable de restituer le timbre de n'importe quel instrument, existant ou à venir, force est de constater que le résultat n'égale pas et sans doute n'égalera jamais le produit de la facture acoustique, patiemment perfectionnée, au cours des siècles, par une sélection naturelle artisanale.

Dans les deux cas, l'art de synthèse peut surprendre voire flatter les sens mais bientôt il les fatigue. Par-dessus tout, il lui manque ce supplément d'âme qui distingue l'Art de la Technique. Or la société moderne est déjà bien assez technique comme cela et ce n'est pas la peine d'en rajouter; mieux vaut honorer les bons artisans et les vrais artistes.