Faits divers
Gammes et Tempéraments
Sommaire
[ afficher ]- Construction de la gamme pythagoricienne
- 1) Un cycle de 6 quintes (7 notes)
- 2) L'alternance des quintes ascendantes et des quartes decendantes
- 3) Les altérations
- 4) Un cycle de 20 quintes (21 notes)
- 5) Problèmes de transpositions
- 6) Un cycle de 34 quintes (35 notes)
- 7) Réduction de la gamme pythagoricienne à 12 notes
- 8) L'imbroglio des octaves, des quintes et des tierces
- Une gamme naturelle ?
- Tempérer les quintes pour respecter l'octave
- 1) Une solution extrême : la quinte du loup
- 2) Un compromis célèbre : le tempérament de Werckmeister Ⅲ (1691)
- 3) Un compromis prometteur : le tempérament égal
Cet article, modifié pour la cause, a fait l'objet d'une radiodiffusion en direct sur la Radio Parfaite, l'antenne officielle du Festival musical du Printemps des Arts de Monte-Carlo, le 4 avril 2018. L'écho différé est disponible ici : .
Personne ne conteste raisonnablement que la théorie musicale repose sur les principes de l'acoustique physique. En privilégiant les rapports consonants que les fréquences des sons entretiennent entre elles, l'acoustique fait appel, à son tour, à l'étude des fractions simples. Cependant, il n'y a que les mathématiciens pour s'intéresser à l'arithmétique musicale et les physiciens pour invoquer les lois de l'acoustique. Les musiciens ne se soucient généralement ni de l'une ni de l'autre : peu concernés par les sciences exactes, ils estiment avec quelques raisons qu'ils n'en ont nul besoin et qu'il leur suffit d'obéir à leur instinct. De fait, la théorie musicale, ils l'apprennent le plus souvent à un âge précoce (le plus tôt est le mieux) où aucune des bases scientifiques nécessaires n'est acquise. Lorsqu'ils seraient en âge de les assimiler, leur formation musicale est suffisamment engagée pour qu'ils n'éprouvent plus le besoin d'y revenir, ne serait-ce que pour asseoir ce qu'ils ont appris sur des bases logiques incontestables. Il vaut peut-être mieux qu'il en soit ainsi car ils s'apercevraient que cette logique a souvent fait défaut à l'enseignement qu'ils ont reçu. Cette chronique s'inspire, en particulier, quoique très librement, de la lecture de quelques textes du grand musicologue français, Jacques Chailley (1910-1999). La sentence qui ouvre ses leçons dispensées en Sorbonne (Formation et transformation du langage musical - Intervalles et échelles), peut certes interpeller même si elle n'a guère été suivie d'effets :
Il règne dans la Musique un ordre admirable. Mais on a pu l'accuser de désordre par la faute de ceux qui ont entrepris de l'expliquer. (Aristoxène, Elém. Harm.)
Déjà en 1722, les premiers articles de Jean-Jacques Rousseau, parus dans l'Encyclopédie de d'Alembert et Diderot, déploraient les contresens qui commençaient à se répandre dans la théorie musicale. 300 ans plus tard, force est de constater qu'aucun travail sérieux de rationalisation n'a été entrepris, comparable à celui que se sont imposées toutes les théories scientifiques, au tournant des années 1900. Rien qu'une simplification de la gestion des clefs et des altérations ne serait pas un luxe mais il semble aussi difficile de réformer l'orthographe musicale d'usage que son équivalent français. Les musiciens (comme les académiciens) ont leurs raisons que nous tenterons de comprendre car, de toutes façons, ils auront toujours le dernier mot.
Comme son titre l'indique, cette chronique ne s'occupe que de gammes et de tempéraments. Elle ne poursuit pas l'objectif de prospecter les réformes possibles de la syntaxe musicale. Seulement évoquées ponctuellement, celles-ci feront l'objet d'un prochain article.
Entre justesse et transposition
1) Justesse
La musique étant l'art d'ordonner les sons, la justesse de leurs superpositions harmoniques et/ou de leurs enchaînements mélodiques semblent a priori primordiales. En première approximation, largement suffisante à ce stade, un son se distingue d'un bruit du fait qu'il est périodique, sollicitant nos tympans à la fréquence de f impulsions par secondes (Pour une oreille "normale", f doit être comprise entre 16 Hz et 16000 Hz). Il est grave si f est basse et aigu si elle est élevée.
On a identifié depuis très longtemps la règle essentielle de la consonance : deux sons résonnent en harmonie si le rapport de leurs fréquences fondamentales s'exprime par une fraction simple. En dehors du trivial unisson, on retient prioritairement les rapports : 2/1 (octave), 3/2 (quinte), 4/3 (quarte), 5/4 (tierce majeure), 5/3 (sixte majeure), 6/5 (tierce mineure) et 8/5 (sixte mineure).
La justification de cette règle est d'ordre physique : un son fait vibrer l'air à sa fréquence fondamentale, f, mais aussi et simultanément aux fréquences multiples (dites harmoniques), 2f, 3f, 4f, ..., avec des intensités relatives (et accessoirement des déphasages) qui dépendent (du timbre) de l'instrument émetteur (On se limite aux instruments harmoniques qui vibrent de façon parfaitement élastique, une corde de violon par exemple; une cloche en bronze ou un xylopohone ne rentrent pas dans cette catégorie). Deux sons distincts sont particulièrement consonants lorsqu'ils partagent un nombre "appréciable" de composantes harmoniques. Voici les exemples les plus simples :
- Le son situé à l'octave (supérieure) du son de référence possède le spectre des fréquences, 2f, 4f, 6f, ..., toutes présentes dans le spectre de référence. La consonance est parfaite dans ce cas.
- Le son situé à la quinte (supérieure) du son de référence possède le spectre des fréquences, 3f/2, 3f, 9f/2, 6f, ... . Il partage la moitié des composantes du son de référence. La consonance est excellente dans ce cas.
- Le son situé à la quarte (supérieure) du son de référence possède le spectre des fréquences, 4f/3, 8f/3, 4f, 16f/3, ... . Il partage le tiers des composantes du son de référence. La consonance est encore très bonne.
- Et ainsi de suite pour une consonance qui s'appauvrit progressivement sans que l'on soit en mesure de quantifier cette dégradation avec précision, d'autant que la physiologie de la chaîne qui relie l'oreille au cerveau a aussi son mot à dire.
L'intervalle entre deux sons est défini selon le rapport (et non la différence !) de leurs fréquences respectives. Cette règle géométrique (et non arithmétique !) découle du fait que l'oreille humaine est sensible au phénomène d'octave : une mélodie répétée en doublant les fréquences de chaque note sonne comme la mélodie primitive mais en plus aiguë, à l'octave supérieure. Cela reste vrai si on multiplie les fréquences des notes par un facteur constant quelconque, x (>1; si x < 1, la deuxième mélodie sonnera en plus grave). Une autre manière d'exprimer la propriété invoquée de l'oreille consiste à dire que sa réponse en fréquence est logarithmique : des sons émis en séquence, dont les fréquences croissent (ou décroissent) selon une progression géométrique, f, x f, x2 f, x3 f, ..., sont perçus comme "équidistants".
On définit, sur cette base, l'intervalle séparant deux sons de fréquences, f1 et f2 : Int = 1200 ℓg(f2/f1) (mesuré en cents), où ℓg désigne le logarithme en base 2. Connaissant l'intervalle qui sépare deux sons, il est possible de retrouver leur rapport fréquentiel, il suffit d'inverser la formule précédente sous la forme, f2/f1 = 2Int/1200. Voici les valeurs exactes de quelques intervalles consonants :
| unisson (1/1) | octave (2/1) | quinte (3/2) | quarte (4/3) | tierce majeure (5/4) | sixte majeure (5/3) | tierce mineure (6/5) | sixte mineure (8/5) |
|---|---|---|---|---|---|---|---|
| 0 (cents) | 1200 (cents) | 701.955 (cents) | 498.045 (cents) | 386.314 (cents) | 884.359 (cents) | 315.641 (cents) | 813.686 (cents) |
Le défaut de consonance, en tous cas le désagrément qu'il provoque à l'audition, est largement imputable au phénomène physique de battement. Lorsqu'on superpose deux sons de fréquences nettement différentes, tout se passe bien, l'oreille les perçoit distinctement. Lorsque les fréquences se rapprochent, un battement apparaît sous la forme d'une ondulation de l'intensité résultante, à la fréquence, fbatt = f2 - f1. Le temps que dure une oscillation complète s'appelle la période de battement, Tbatt = 1/(f2 - f1). Ce phénomène peut présenter une gêne pour l'oreille , à la manière d'une lumière stroboscopique perturbante pour l'oeil. La plage des fréquences gênantes, fbatt, se situe (très) approximativement entre 5 Hz et 25 Hz : en-deçà, le battement est d'autant mieux toléré que les notes se suivent et s'estompent à un rythme soutenu et, au-delà, l'oreille ne détecte plus le phénomène, incapable de suivre la cadence des oscillations. On traduit cette plage fréquentielle, en termes d'intervalles, en partant de la formule, fbatt = f2 - f1 = f1 (2Int/1200-1) ≅ f1 0.693 (Int/1200). On en déduit la zone critique : 10390/f1 < Int < 43290/f1. Dans l'octave du milieu, f1 est de l'ordre de 260 Hz d'où on a : 33 (cents) < Int < 165 (cents). Une ou deux octaves plus bas, ces limites devraient être corrigées à la hausse.
Note. Les octaves inférieures sont très fréquentées par l'orgue qui est, de fait, l'instrument le plus sensible aux battements. Le problème est encore aggravé par le fait que c'est aussi l'instrument où les notes sont souvent (main)tenues le plus longtemps. Les organistes sont donc particulièrement concernés par les problèmes de justesse et de tempérament (cf infra). Toujours, à l'orgue, le phénomène de battement est exceptionnellement cultivé : la plupart des instruments possèdent un registre particulier qu'on nomme "voix céleste", qui implique des tuyaux volontairement accordés sur des fréquences voisines. Le battement y est alors cultivé pour ses trémolos évocateurs (Olivier Messiaen : Le Banquet céleste).
Les intervalles usuels de types "courts", 2de mineure (do-réb) et 2de majeure (do-ré), sont concernés par la limite calculée et ils sont, de ce fait, classés parmi les intervalles dissonants. Les intervalles plus "longs" semblent y échapper, d'où on pourrait s'étonner que la quarte augmentée (do-fa#) et la quinte diminuée (do-solb) soient également rangés parmi les intervalles particulièrement dissonants.
La réponse est que les battements ne concernent pas que les fréquences fondamentales des sons mais aussi celles de leurs harmoniques. Si les sons étaient dépourvus d'harmoniques, par exemple émis par des diapasons sinusoïdaux (pas très musicaux évidemment car complètement détimbrés), alors, effectivement, aucun battement secondaire n'existerait. Mais l'existence des harmoniques a pour conséquence que des battements secondaires peuvent se produire entre harmoniques de rangs plus ou moins élevés. Considérons les exemples de la superposition d'un moderne do4 (f1 = 261.63 Hz) et de sa tierce majeure, pure (f2 = 5/4 x 261.63 = 327.04 Hz) ou tempérée (f2 = 1.26 x 261.63 = 329.65 Hz).

Le coin supérieur gauche correspond à l'intervalle entre les fondamentales
Lorsque le rapport fréquentiel, f2/f1 = m/n, est simple et exact, par exemple 1.25 = 5/4 (cas de la tierce majeure pure), aucun battement, fondamental ou secondaire, n'est à redouter. Cela apparaît sur la figure ci-contre (à gauche) qui mentionne les intervalles (en cents) entre les premières combinaisons d'harmoniques possibles : ils sont soit supérieurs à 300 cents soit nuls, dans les deux cas en-dehors de la zone gênante. Si, pour quelque raison que ce soit, le rapport 5/4 n'est pas absolument respecté, par exemple s'il vaut 1.26 (ce qui est le cas de la moderne tierce majeure tempérée), la même figure (à droite) montre que la consonance est notamment menacée par un battement entre les composantes de fréquences 5 f1 et 4 f2 (coin inférieur droit). Ce battement prend la forme d'une ondulation de l'intensité, à la fréquence, n f2 - m f1, de l'ordre de 10 Hz dans l'exemple considéré. Le phénomène apparaît nettement sur la figure ci-dessous (à droite).
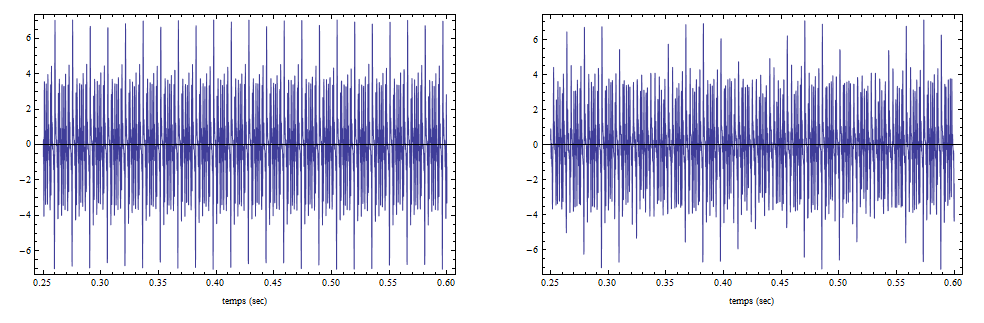
Le tableau suivant illustre quelques cas de figures qui seront détaillés en cours de texte. On peut y entendre plusieurs enchaînements d'un do4, synthétisé sur base d'une sinusoïde fondamentale et de quatre sinusoïdes harmoniques, avec une notes choisie parmi un ensemble de cinq, puis la superposition des deux. Ces 5 notes sont, dans l'ordre des lignes, un réb pythagoricien, un sol pythagoricien (quinte parfaite), un sol pythagoricien faussé d'un neuvième de ton (quinte fausse), un mi pythagoricien (tierce majeure impure) et un mi zarlinien (tierce majeure pure) :
| Rapport | Intervalle (cents) | Fréquence (Hz) | Battement ? | |
|---|---|---|---|---|
| do4 | 1/1 | 0 (cents) | 261.626 (Hz) | sans objet |
| réb (pyth) | 256/243 | 90.225 (td) | 275.623 | fondamental |
| sol (pyth) | 3/2 | 701.955 | 392.439 | non |
| sol (faux) | 1.5197 | 724.612 | 397.609 | harmonique |
| mi (pyth) | 81/64 | 407.82 | 331.12 | harmonique |
| mi (pur) | 5/4 | 386.314 | 327.032 | non |
Note. L'incrimination du battement dans l'explication du phénomène de dissonance est due au physicien von Helmholtz (1821-1894) mais il est juste de dire qu'elle ne fait plus l'unanimité depuis que le psychologue Carl Stumpf (1848-1936) a montré, dans une série d'expériences psychoacoustiques, qu'il pouvait y avoir (perception de) dissonance sans battement. Le musicologue Heinrich Husmann (1908-1983) a alors préconisé de renverser le problème en affirmant que c'est la consonance qui est perçue lorsque les sons superposés présentent un maximum d'harmoniques communs. Cette diversité d'opinions est typique des disciplines où des chercheurs aux formations aussi différentes tentent de se mettre d'accord.
2) Transposition
Transposer un air, c'est multiplier la fréquence de chacune de ses notes par un facteur constant, x, ou, ce qui revient au même, c'est translater chaque note d'un intervalle constant, 1200 ℓg(x) (cents). On recourt à la transposition toutes les fois que l'on veut jouer un air sur un instrument (éventuellement la voix) dont la tessiture diffère de celle de l'instrument prévu originellement. On pourrait s'étonner que des musiciens réputés sérieux s'encombrent d'une telle notion : si le compositeur a pris la peine d'écrire son oeuvre pour un instrument donné, dans une tonalité précisée, c'est pour qu'elle soit jouée de cette façon et pas d'une autre. Cette latitude a pourtant toujours existé, ne fut-ce que pour satisfaire de nombreux amateurs désireux d'adapter des oeuvres pas trop difficiles du répertoire à leur usage personnel. Les chanteurs (ou les chanteuses !) de toutes tessitures sont également demandeurs, qui rêvent d'interpréter "leur" Voyage d'Hiver de Schubert, même s'ils ne sont pas ténors comme la partition l'a prévu.
Apparentée à la transposition mais fondamentalement plus importante, la modulation est utilisée par le compositeur toutes les fois qu'il veut agrémenter un mouvement en cours par une diversion durable, dans une tonalité contrastée, en changeant de tonique et/ou de mode. Ce procédé, désormais omniprésent en musique dite classique, a tôt inspiré des curiosités didactiques telles Le Petit Labyrinthe harmonique, pour orgue, attribué à J-S Bach (BWV 591) mais plus probablement l'oeuvre de Johann David Heinichen ou encore, plus tardivement, les Deux Préludes (opus 39), dans tous les tons majeurs, écrit par le jeune Beethoven à l'époque où il était encore l'élève de Neefe. Bien qu'annoncé en ré mineur, l'un des premiers grands chefs-d'oeuvre à jouer avec l'incertitude tonale est une oeuvre isolée de J-S Bach, la Fantaisie chromatique et Fugue, BWV 903.
Justesse et transposition sont mathématiquement incompatibles et ce conflit a préoccupé les musiciens à toutes les époques, depuis la Renaissance. Epris de justesse, les premiers compositeurs baroques ont renoncé à la modulation intégrale mais leurs successeurs ont fait le choix inverse, abandonnant la justesse à tout prix, au bénéfice d'une plus grande liberté d'écriture. Les ressorts de ce revirement vont nous occuper.
Construction de la gamme pythagoricienne
On crédite habituellement Pythagore (né vers -580) et plus probablement ses élèves, d'avoir développé le premier modèle de gamme musicale. Ils l'ont fait en privilégiant les deux intervalles les plus immédiatement consonants, l'octave et la quinte.
La gamme d'essence pythagoricienne est ancienne mais elle n'a, au fond, rien perdu de son actualité. Elle a, en particulier, conditionné l'orthographe musicale telle que nous la connaissons encore aujourd'hui. Sa construction s'effectue en deux temps :
- On commence par construire un ensemble de notes entretenant un rapport de quinte juste au sein d'une octave unique, c'est l'objet de cette longue section.
- On tente ensuite d'étendre le schéma trouvé aux octaves voisines, ce sera l'objet de la section suivante, relative au tempérament.
L'incommensurabilité (géométrique, pas arithmétique, cf supra !) entre les intervalles d'octave et de quinte rend cette double opération irréalisable en toute rigueur, d'où un compromis s'impose qui reste à définir.
1) Un cycle de 6 quintes (7 notes)
Le schéma pythagoricien génère les notes successives, au sein de l'octave de référence, [f0 - 2f0[, en suivant la procédure élémentaire suivante :
- Partant d'une note de base, de fréquence f0, on définit les notes situées aux quintes ascendantes successives. Pour ce faire on multiplie itérativement f0 par 3/2, ce qui génère la suite des (notes de) fréquences, fk = f0 (3/2)k (k = 0, 1, 2, ..., 6). Toutes ces notes, distantes d'un intervalle de quinte, sont consonantes.
- Sauf f0 et f1 = 3/2 f0, aucune note n'appartient à l'octave de base, [f0 - 2f0[, d'où on les y ramène par autant de division par 2 qu'il est nécessaire. Ces divisions ne modifient pas la consonance des notes puisqu'elles ne font que les transporter une octave plus bas (éventuellement plusieurs). On obtient ainsi la suite de (notes de) fréquences, fk = f0 (3/2)k/2Floor[k ℓg(3/2)] (k = 0, 1, 2, ..., 6), soit, dans le détail, f0, f0 31/21, f0 32/23, f0 33/24, f0 34/26, f0 35/27 et f0 36/29, toutes consonantes, au motif imagé que, par contagion, "les amis de mes amis sont aussi mes amis".
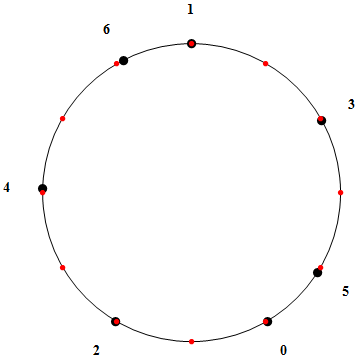
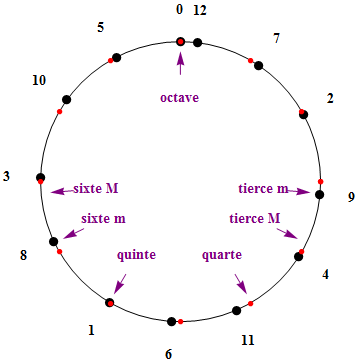
Une simplification est utile, à ce stade : plutôt que de raisonner en termes de fréquences, il est bien plus commode de considérer les intervalles entre les notes. On permet ainsi une description graphique au moyen d'un cercle dont le périmètre complet représente l'intervalle d'octave. Sur la figure ci-contre, 12 points rouges graduent ce cercle de 0 à 1200 (cents), par pas de 100 (cents). Dans cette représentation, l'intervalle de quinte ascendante, Q = 1200 ℓg(3/2) = 701.95 (cents) correspond à un arc de cercle de 3.67543 radians (soit 210° 35' 12" ou encore 0.584963 tour de circonférence), orienté dans le sens horlogique. L'idée est alors de choisir une origine a priori quelconque pour la note de départ (notée 0 sur la figure) puis de positionner les autres notes (1, 2, ..., 6) successivement une quinte plus haut. La suite des intervalles, mesurés depuis l'origine, se note Mod[k Q, 1200] (k = 0, 1, 2, ..., 6) = { 0, 701.955, 203.91, 905.865, 407.82, 1109.78, 611.73} (cents), où la fonction Mod rappelle que lorsqu'on dépasse 1200 cents, on ne considère que l'excédent, ce qui correspond bien à l'idée d'une réduction à une octave unique.
Note. Dans la suite nous serons amenés à poursuivre la construction précédente donc à empiler un nombre croissant de quintes. A aucun moment on ne retombera sur une note déjà trouvée car l'intervalle, Q = 1200 ℓg(3/2), est un nombre irrationnel. Il en résulte que le nombre des notes que l'on peut définir par ce procédé, au sein de l'octave, ne connaît pas de limite et qu'il faudra tôt ou tard dicter un critère limitant. Par ailleurs, le lecteur attentif aura noté que le principe même de la construction de la gamme entraîne à effectuer plusieurs tours du cercle des quintes afin de positionner les notes. Cela ne devrait pas poser de problème à tous ceux qui ne s'étonnent pas de devoir lire l'heure sur un cadran de montre qui indique 5 heures tous les jours de la semaine, matin et soir, sans autre explication. Dans tous les cas, le contexte résout les ambiguïtés liées à cette représentation modulaire.
Sur la figure précédente, on est parti (avec une idée derrière la tête !) du point 0, situé une quinte en-dessous du point 1, lui-même situé au sommet du cercle. Une quinte descendante correspond au rapport inverse (2/3) donc au même arc de cercle mais orienté dans l'autre sens. Au bilan, les six quintes ascendantes successives sont donc, 0-1, 1-2, 2-3, ... et 5-6. Ne confondez pas l'ordre des 6 quintes, qui sont des intervalles, avec celui des 7 notes qu'elles définissent et qui parcourent l'octave dans l'ordre horlogique des fréquences croissantes, 1, 3, 5, 0, 2, 4, 6. Le choix de la note n°1 comme point de départ est compatible avec l'énumération classique, do, ré, mi, fa, sol, la, si; il n'est pas essentiel mais il permet de respecter la tradition.
La première chose à faire, dans l'immédiat, est de justifier le choix fait de se limiter (provisoirement !) à 7 notes. Ne répondez pas que c'est parce que tout le monde sait bien que la gamme occidentale comporte 7 notes, c'est précisément ce que nous tentons de justifier, au moins heuristiquement !
2) L'alternance des quintes ascendantes et des quartes descendantes
Empiler des quintes et les ramener à l'octave de référence n'est pas la façon la plus élégante de procéder, d'autant qu'à force de multiplier itérativement la fréquence de base par 3/2, on se retrouve vite dans le domaine des ultrasons ! La variante suivante est équivalente mais plus réaliste. Le début est identique : on conserve la note de base, de fréquence, f0, mais cette fois, on alterne une quinte ascendante et une quarte descendante. La quarte est le complément naturel de la quinte : un son situé une quarte en-dessous d'un son de fréquence, f0, possède, par définition, la fréquence 3f0/4; il se situe donc une octave en-dessous de la quinte ascendante. On représente une quarte descendante, en se déplaçant de q = 1200 ℓg(4/3) = 498.045 (cents) dans le sens contre-horlogique, ce qui revient bien au même que d'augmenter d'une quinte (à une octave près). Encore dit autrement, une quinte (701.95) plus une quarte (498.045) vaut une octave 1200 (cents).
Remplacer l'empilement des quintes par l'alternance répétée d'une quinte ascendante et d'une quarte descendante ne change donc rien au résultat du calcul de la suite des fréquences des notes engendrées (Multipliez les fractions si vous doutez encore!). Cependant, on en tire ce bénéfice qu'en partant de la fréquence basse, f0, de l'octave, [f0 - 2f0[, il n'est plus nécessaire de changer artificiellement d'octave, pendant les 6 premières itérations. Les 7 notes de la gamme heptatonique apparaissent spontanément, dans l'énumération dite "par les quintes", fa, do, sol, ré, la, mi, si. La note de départ, fa, ne joue aucun rôle particulier dans ce processus et l'on pourrait partir de n'importe quelle autre note mais si l'on veut retarder autant que possible l'apparition des altérations, donc retrouver en séquence les 7 notes traditionnelles, alors il convient de partir de cette note-là.
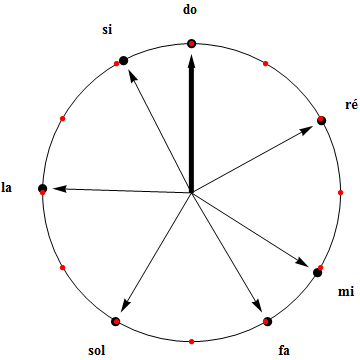
La figure ci-contre nomme les 7 notes définies par l'empilement de 6 quintes, au départ de la note fa, et elle souligne les intervalles qui les séparent par un système de flèches. Deux types d'intervalles apparaissent (ton et demi-ton diatonique, on y reviendra), qui définissent le mode (de do) majeur. Ne confondez pas :
- l'ordre des quintes ascendantes : fa, do, sol, ré, la, mi, si, où la tonique (do, dans ce cas) occupe obligatoirement la deuxième position et
- l'ordre des fréquences croissantes (du grave vers l'aigu) : do, ré, mi, fa, sol, la, si, où la tonique occupe, cette fois, la première position.
Les musiciens inscrivent traditionnellement ces notes sur une portée comportant (au moins) 5 lignes, dans l'ordre vertical ascendant des fréquences croissantes. Cette portée peut être vue comme une échelle un peu spéciale dont les échelons successifs (les lignes et les interlignes) sont de hauteurs ... inégales, cela apparaît clairement sur le cercle des quintes (Les intervalles, mi-fa et si-do, sont, à vue de nez, deux fois plus court que les autres). Vous commencez à comprendre pourquoi il faut commencer le solfège le plus tôt possible : seul un jeune enfant peut s'accommoder, sans broncher, d'une échelle pareille. Reconnaissons que cela ne perturbe aucun musicien aguerri, les autres ayant abandonné depuis longtemps. Trêve d'ironie, la succession des flèches définit les degrés de la gamme et c'est bien pratique : si do est la tonique, de degré Ⅰ, la quarte (fa) occupe le degré Ⅳ, la quinte (sol) occupe le degré Ⅴ et l'octave (do supérieur) le degré Ⅷ, les noms sont évocateurs. Sur une portée, on monte d'un degré toute les fois qu'on passe d'une ligne à l'interligne suivante (ou l'inverse) comme représenté sur la figure ci-dessous.

Note. Dans tous les domaines de l'activité humaine, y compris scientifiques, les traditions sont porteuses de conventions séculaires (mal)heureuses, impossibles à changer tant elles sont ancrées dans les habitudes. La notation musicale n'échappe pas à cette constatation. Cette figure utilise la convention anglo-saxonne de représenter les notes par des lettres : C = do, D = ré, E = mi, F = fa, G = sol, A = la et B = si (mais les germanophones utilisent H !). Cet ordre étrange pourrait laisser penser que les anglo-saxons démarrent l'octave à partir du la mais ce n'est pas le cas. Dans tout système de notation, chaque note est, en théorie, porteuse d'un indice qui rappelle le numéro de l'octave à laquelle elle appartient (la3, la4, la5, ...). Les américains respectent la recommandation internationale qui situe le diapason moderne (la = 440 Hz) dans l'octave n°4, ce que ne font pas les latins qui en sont encore à le situer dans l'octave n°3. Bref, do3 = C4, ré3 = D4, mi3 = E4, fa3 = F4, sol3 = G4, la3 = A4, si3 = B4 et on recommence une octave plus haut, do4 = C5, etc.
Dans l'immense majorité des cas, une partition représente graphiquement les notes sur une portée, une aide au déchiffrement des interprètes. Les rares exceptions concernent les musiques expérimentales (Stockhausen) et/ou algorithmiques (Xenakis). Dans le cadre théorique lié à l'enseignement de la musique, l'appellation des notes diffère cependant selon les écoles, recourant à une version syllabique (pays latins et Russie) et/ou alphabétique (pays anglo-saxons). On a même rêvé d'une écriture chiffrée.
- Les systèmes syllabique et alphabétique ont coexisté, en France, jusqu'à ce que les théoriciens décrètent (vers 1700 ?) qu'ils faisaient double emploi, d'où le système syllabique s'est imposé. Dans l'article "Solfier" de l'Encyclopédie, le philosophe des Lumières, Jean-Jacques Rousseau a déploré cet abandon, rappelant mais apparemment en vain, que les deux notations poursuivent des buts différents : pour faire simple, la notation alphabétique (C, D, E, ...) s'adresse à l'oeil qui voit les notes couchées sur une partition ou les touches d'un clavier tandis que la notation syllabique s'adresse à l'oreille qui entend la solmisation de ces notes (do, ré, mi, ...). La tradition française ayant opté pour une solmisation fixe (un do, altéré ou non, se chante do, etc), la distinction devenait, de fait, superflue.
- Rousseau était, au contraire, adepte d'une solmisation mobile (ou flottante), encore en vogue dans les pays anglo-saxons, ne se servant des syllabes que comme de paroles conventionnelles sur l'air à chanter; peu importe que la tonique soit un do ou un mi, il n'y a lieu de respecter que les intervalles. Vous ne faites rien d'autre lorsque vous chantez (juste !) la-la-la-la ! Le point de vue de Rousseau a été contesté par Jérôme Joseph de Momigny, dans un autre article paru dans l'Encyclopédie.
- Une troisième voie existe qui n'a guère fait fortune. Si l'on avait confié le principe de la notation musicale à des mathématiciens, il est probable qu'ils auraient mis au point un système rationnel chiffré respectant les intervalles entre les notes. C'est encore Jean-Jacques Rousseau qui s'est risqué dans l'aventure. Ni mathématicien ni vraiment musicien (du moins professionnel, ce qui n'a pas empêché qu'on lui ait confié, et non à Rameau, les articles sur la musique dans l'Encyclopédie), il a envoyé à l'Académie un projet de notation de ce type. Plutôt mal conçu, il a été recalé pour de mauvaises raisons et il est tombé aux oubliettes ... sauf que, "relooké", il refait périodiquement surface (en particulier en Chine !), apprécié pour les facilités qu'il offre dans le cadre de l'initiation des enfants. Si vous voulez approfondir la question, reportez-vous au document intitulé Le Devenir du Système de Notation musicale de Jean-Jacques Rousseau, issu des recherches du musicologue canadien, Claude Dauphin.
- J'ai rappelé par ailleurs (dans Musique 2001) et j'approfondirai (dans La Notation musicale) le principe d'une variante théoriquement supérieure, reposant sur l'arithmétique en base 12, mais les musiciens ne sont pas près de l'adopter, officiellement parce qu'aucune méthode chiffrée ne peut, à leur avis, rendre justice aux subtilités du langage musical et officieusement parce qu'ils sont conservateurs dans l'âme. Je n'en veux pour meilleure preuve que même lorsqu'ils entrent à l'école dodécaphonique, domaine où l'arithmétique en base 12 prend tout son sens, ils continuent d'écrire sur une portée avec des dièses et des bémols, qui ne remplissent pourtant plus aucune fonction tonale. Pour la petite histoire, sachez qu'il existe depuis 1944 (euh 1160 !) une pittoresque Dozenal (formerly Duodecimal) Society of America qui prône, sans grand succès, la généralisation du système arithmétique en base 12 dans tous les secteurs d'activité de la société. Elle a reçu, en 1948, un opuscule rédigé par Velizar Godjevatz (1898-1986), un musicien américain formé à Oxford et Berlin, et mettant en évidence les avantages "évidents" d'une notation musicale chiffrée en base 12, ambitionnant de supprimer purement et simplement les altérations et les clefs (Je vous ai bricolé un facsimile du texte complet, normalement introuvable sauf par les soins de la bibliothèque digitale HathiTrust mais si vous manquez de temps, sachez que je vous ferai prochainement l'article). Au plan syntaxique, la démonstration semble convaincante, tel fut en tous cas l'avis du célèbre critique musical, George Bernard Shaw, sollicité par la Société en tant que rapporteur.
3) Les altérations
Sept notes par octave, c'est trop peu ! On aimerait poursuivre l'alternance des quintes et des quartes et ainsi définir de nouvelles notes qu'il faut pouvoir nommer. Leur donner des noms inédits ne serait pas une bonne idée, pensez aux compositeurs et aux interprètes qui devraient gérer un vocabulaire de plus en plus encombrant ! Dès le Moyen-Age, les théoriciens de la musique ont trouvé une solution astucieuse, toujours en vigueur, c'est le principe de l'altération.
Reconsidérons l'alternance des quintes ascendantes et des quartes descendantes, au départ de la note, fa, et reportons-la sur une portée. La figure suivante est facile à décoder : une quinte fait monter de 5 degrés, une quarte fait descendre de 4 degrés, lignes et interlignes compris, et les 7 notes traditionnelles apparaissent bien dans l'ordre des quintes, fa, do, sol, ré, la, mi, si. On constate qu'une quinte supplémentaire amènerait à dépasser l'octave de référence (note blanche sur la figure) d'où une réduction d'une octave s'impose, qui semble ramener la nouvelle note au niveau du fa initial (on descend de 8 degrés). Cependant cette note ne peut être un vrai fa car elle n'en possède pas la fréquence. On calcule aisément l'intervalle qui sépare ces deux notes cependant voisines en effectuant les produits successifs correspondant aux 4 quintes ascendantes (3/2)4, entremêlées aux 3 quartes descendantes (3/4)3, enfin à l'abaissement d'une octave (1/2) : Int = 1200 ℓg(37/211) = 113.685 (cents) (ce qui correspond à un rapport de fréquences valant, 37/211 = 1.06787). On appelle "fa dièse = fa#" cet autre fa. En poursuivant l'alternance, on engendrerait de nouvelles notes diésées, séparées de "leur" note naturelle par le même intervalle, appelé demi-ton chromatique, tc = 113.685 (cents).

La portée précédente peut être prolongée, vers la droite, autant de fois qu'on le souhaite : le cycle, fa, do, sol, ré, la, mi, si, est suivi d'un deuxième cycle avec dièses, fa#, do#, sol#, ré#, la#, mi#, si#, puis par un troisième cycle, avec doubles dièses, fa##, do##, sol##, ..., si##, etc. La règle précédente demeure valable : chaque fois qu'on ajoute un dièse à la note naturelle, on augmente l'intervalle de tc.
Rien n'empêche de prolonger la portée vers la gauche, au départ du fa initial : une première quarte ascendante génère une nouvelle sorte de si qu'on distingue du si habituel en lui collant cette fois un bémol (b). On calcule aisément que l'intervalle qui sépare le si naturel du sib vaut encore un demi-ton chromatique et cela reste vrai à tous les niveaux : un bémol abaisse la note de 113.685 (cents). Le lecteur égaré va pouvoir se récupérer grâce à la figure suivante, qui empile 20 quintes ascendantes à partir de fab.
4) Un cycle de 20 quintes (21 notes)
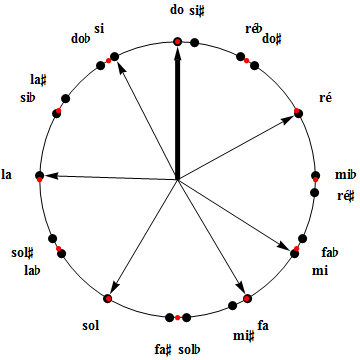
L'empilement de 20 quintes (ou l'alternance équivalente de quintes et de quartes), ramenées à une octave unique, détermine 21 notes, naturelles ou simplement altérées. Il n'est pas nécessaire de s'embarrasser des calculs de fractions car nous savons, une fois pour toutes, qu'une quinte ascendante correspond à une rotation de Q = 701.95 (cents) dans le sens horlogique. Les 21 notes se notent comme suit, dans l'ordre des quintes et au départ de fab (histoire de se conformer à l'usage, cf supra) : fab, dob, solb, réb, lab, mib, sib, fa, do, sol, ré, la mi, si, fa#, do#, sol#, ré#, la#, mi#, si#. Ne le confondez pas avec l'ordre selon les fréquences (du grave vers l'aigu) que vous lisez en parcourant le cercle dans le sens horlogique, selon l'usage à partir du do (do, si#, réb, do#, ré, etc).
Les intervalles qui séparent les 21 notes sont de deux types principaux :
- Le demi-ton diatonique valant, td = 1200 ℓg(28/35) = 90.225 (cents), sépare les notes naturelles mi-fa et si-do.
- Le demi-ton chromatique valant, tc = 1200 ℓg(37/211) = 113.68 (cents), sépare les notes naturelles de leurs variantes simplement altérées (en # ou en b), par exemple, ré-ré#.
Les autres intervalles observés sont des combinaisons linéaires de ces deux-là. Par exemple :
- Le ton, valant, T = td + tc = 1200 ℓg(32/23) = 203.91 (cents), sépare les notes naturelles do-ré, ré-mi, fa-sol, sol-la et la-si. Le mode majeur est donc caractérisé par la succession d'intervalles, T, T, td, T, T, T, td.
- Le petit intervalle séparant les notes, dites enharmoniques, par exemple mib-ré#, vaut, P = tc - td = 1200 ℓg(312/219) = 23.46 (cents), c'est le comma pythagoricien (très approximativement 1/9 de ton).
Note. En théorie moderne, deux notes sont dites enharmoniques (ou synonymes) lorsqu'elles correspondent à une même touche du clavier également tempéré (ex. do# et réb). Ce n'est manifestement pas le sens primitif, l'enharmonie ayant existé bien avant l'avènement du tempérament égal, d'où il semble possible d'évoquer "l'abscence d'harmonie" : la petitesse du comma pythagoricien empêche, de fait, ces notes de sonner en harmonie, revoyez les explications relatives au phénomène de battement. - La quinte vaut, Q = 3tc + 4td = 701.955 (cents), la quarte vaut, q = 2tc + 3td = 498.045 (cents) et l'octave vaut naturellement, 5tc + 7td = 1200 (cents).
Note. Bien que la logique ait peu à dire sur la question, vous trouverez dans la littérature au moins une autre "explication" du fait qu'on se soit limité à 7 (noms de) notes, recourant aux symboles d'altérations pour les autres.
- Si l'on suit le cycle des quintes, en partant de fa, on observe qu'on repasse un peu en-deçà de ce fa après cinq itérations (mi n'est distant de fa que d'un demi-ton diatonique, td = 90.225 (cents)). On pourrait certainement décider de s'arrêter là et formaliser le cycle sur base de 5 (noms de) notes seulement. On obtiendrait une gamme pentatonique (pentaphonique serait plus judicieux), fa, do, sol, ré, la, semblable à celle effectivement en usage dans certaines contrées d'Orient. Dans ce système, mi et si n'existeraient plus que comme des fa et do altérés, qu'on noterait, par exemple (une fantaisie), fa< et do< (situés un demi-ton diatonique plus bas que les fa et do naturels). Dans ce système, un cycle de 15 quintes détaillerait les notes dans l'ordre, fa>, do>, sol>, ré>, la>, fa, do sol, ré, la, fa<, do<, sol<, ré<, la<, où les altérations,> et <, porteraient sur un un demi-ton diatonique, td, ajouté ou soustrait.
- En poursuivant le cycle des quintes, on observe qu'on repasse également à proximité du fa initial après sept itérations (fa# n'est distant de fa que d'un demi-ton chromatique, tc = 113.685 (cents)). On retrouve précisément la gamme heptatonique traditionnelle (heptaphonique serait à nouveau mieux). Les altérations sont, évidemment, les # et les b traditionnels, qui portent, cette fois, sur un demi-ton chromatique, tc.
- Une troisième possibilité résulte d'un nouveau passage à proximité du fa initial après douze itérations (mi# n'est distant de fa que d'un comma pythagoricien, P), c'est la gamme dodécaphonique (tiens, on ne dit pas "dodécatonique" !), pour laquelle une saine logique exigerait qu'on invente 5 nouveaux noms de notes non altérées. Un cycle de 36 quintes se déclinerait dans ce cas (nouvelle fantaisie) : fa↓, do↓, sol↓, ré↓, la↓, mi↓, si↓, U↓, V↓, W↓, X↓, Y↓, fa, do, sol, ré, la, mi, si, U, V, W, X, Y, fa↑, do↑, sol↑, ré↑, la↑, mi↑, si↑, U↑, V↑, W↑, X↑, Y↑, où les altérations, ↓ et ↑, porteraient cette fois sur un comma pythagoricien, P. Une gamme dodécaphonique existe effectivement mais ce n'est pas celle décrite ici, le comma pythagoricien a bien trop mauvaise réputation. La vraie gamme dodécaphonique n'est pas pythagoricienne : elle modifie légèrement les intervalles précédents par le choix du tempérament égal et elle prend alors le nom de gamme chromatique (cf infra).
5) Problèmes de transpositions
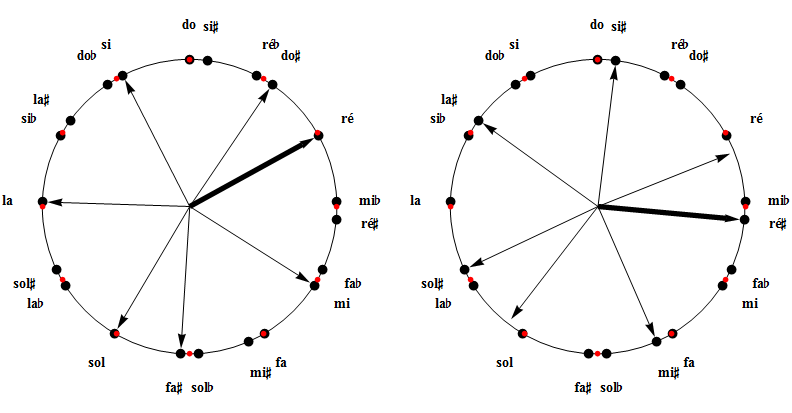
Dans la figure précédente, les repères fléchés signent le mode (de do) majeur. Sauf altérations passagères, les notes utilisées dans ce mode sont celles désignées par les vecteurs, ici les notes naturelles. La figure suivante permet de (re)trouver les notes utilisées dans n'importe quelle autre tonalité majeure : servez-vous du bouton curseur situé en bas pour changer de tonique, les 7 vecteurs tourneront automatiquement.
La figure suivante affiche, à gauche, le cas particulier de la transposition en ré majeur. On constate que les notes constitutives du nouveau ton (do#, ré, mi, fa#, sol, la, si) puisent largement dans l'ensemble des notes naturelles (seules les do et fa sont diésées) : on dit que les tonalités de do et de ré majeur sont proches d'où une modulation peut se faire en douceur. Vérifiez à présent qu'en do# majeur, toutes les notes sont diésées : ce mode est particulièrement éloigné (de do majeur).
La transposition en ré# majeur, visible sur la figure de droite, pose un problème inédit : deux notes manquent manifestement à l'appel. Parmi les 21 tonalités majeures envisageables, six d'entre elles posent ce problème : ré#, mi#, sol#, la#, si# et fab. On génère les notes manquantes en poursuivant l'empilement des quintes, ce qui fait apparaître les notes doublement altérées.
6) Un cycle de 34 quintes (35 notes)
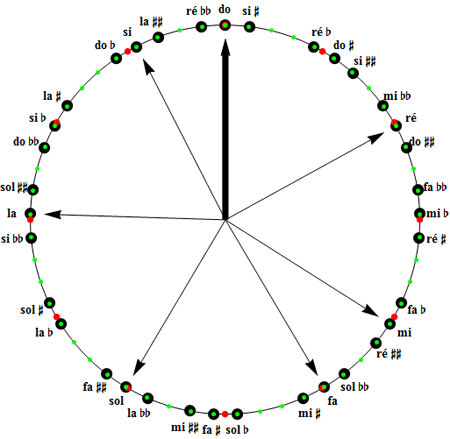
Empilons 34 quintes, par le procédé que nous connaissons, et générons toutes les notes au plus doublement altérées, de fabb à si##. Si vous avez suivi, les notes multiplement altérées sont distantes de la note naturelle de même nom d'autant de demi-tons chromatiques que l'on compte de dièses ou de bémols. Par exemple, les intervalles, fab-fa, fabb-fab, fa-fa# ou fa#-fa## valent tous tc, d'où l'intervalle fabb-fa vaut 2tc. La liste des 35 notes s'écrit comme suit, dans l'ordre des quintes ascendantes :
Le cercle ci-dessus a été étudié en détails pour la première fois par William Holder (1616-1697) dans son traité "A Treatise of the natural Grounds and Principles of Harmony", daté de 1694. Divisé en 53 parties égales (points verts sur la figure), on constate, qu'à peu de choses près, les 35 notes occupent chacune un de ces sites. Holder en a déduit qu'une partition de l'octave en 53 parties égales serait bien proche de l'idéal, sauf que cela commence à faire beaucoup de notes et que, de toute façon, les problèmes de transpositions subsistent dans certaines tonalités, qui exigeraient de nouvelles notes triplement altérées. Personne n'a souhaité s'engager dans cette direction, ni les facteurs de claviers, les accordeurs, les compositeurs ni les interprètes !
7) Réduction de la gamme pythagoricienne à 12 notes
Le système de Holder est impraticable mais il constitue une base de travail qu'on peut espérer simplifier. Un premier élagage consiste à écarter les tonalités exotiques, basées sur une tonique doublement altérée (par exemple do## majeur). On ne conserve donc, dans un premier temps, que les 21 tonalités, de fab à si#.
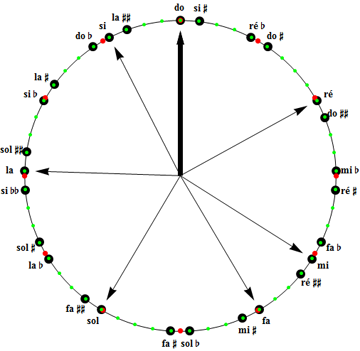
Aux 21 notes correspondantes, nous avons ajouté six notes doublement altérées, sibb, fa##, do##, sol##, ré## et la##, afin de couvrir tous les cas de transpositions majeures. Au bilan (provisoire), nous avons besoin de 27 notes, que nous extrayons de la liste précédente, toujours dans l'ordre des quintes :
Si vous doutez, promenez la tonique de fab à si#, sur la figure dynamique suivante et retenez les notes dont vous avez besoin.
On générerait cette liste tronquée en empilant 26 quintes au départ de sibb, comme représenté ci-dessus. Elle contient l'information relative aux 21 tonalités majeures, de fab à si#; récapitulons-les :
- 7 notes consécutives dans la liste sont constitutives d'une tonalité particulière : en mode majeur, la tonique (degré Ⅰ, en position 2), la note située à sa gauche immédiate (degré Ⅳ) et les 5 notes situées à sa droite immédiate (dans l'ordre, les degrés Ⅴ, Ⅱ, Ⅵ, Ⅲ et Ⅶ). On en déduit immédiatement le nombre de dièses ou de bémols inscrits à la clef. A titre d'exemple, on a souligné, dans la liste, les sous-ensembles de 7 notes constitutives des tonalités extrêmes, fab et si# majeurs : en fab, toutes les notes sont bémolisées et si l'est même doublement tandis qu'en si#, toutes les notes sont doublement diésées sauf mi et si qui ne le sont que simplement. Si l'on s'interdit les notes doublement altérées, il faut s'en tenir aux 15 tonalités allant de dob (toutes les notes sont simplement bémolisées) à do# (toutes les notes sont simplement diésées). Dans tous les cas, il existe une règle simple pour déterminer les notes constitutives d'une tonalité majeure particulière : il suffit de partir de la liste précédente et de cibler 7 notes consécutives de telle façon que la tonique figure en deuxième position. Une règle similaire existe en mode mineur naturel (car il existe des variantes mineures harmoniques et mélodiques que nous ne détaillons pas ici) mais la tonique occupe la cinquième position. Vérifiez, par exemple, que les notes naturelles sont constitutives des tonalités de do majeur ou de la mineur que l'on nomme relatives, pour cette raison.
- Inversement, connaissant le nombre de dièses ou de bémols à la clef, on en déduit dans quelle tonalité on se trouve. Par exemple 4 dièses à la clef, nécessairement fa#, do#, sol# et ré#, sont constitutifs de mi majeur ou de do# mineur et 3 bémols à la clef, nécessairement sib, mib et lab, sont constitutifs de mib majeur ou de do mineur.
Tout cela est résumé dans la grille suivante dont la fenêtre peut être déplacée à loisir de telle manière que la tonique soit positionnée en face de la lettre M, si on est en mode majeur, ou en face de la lettre m, si on est en mode mineur; on visualise instantanément les notes constitutives donc le nombre d'altérations. A titre d'exercice, vérifiez que les seules tonalités majeures qui acceptent les notes sol, ré, la et mi sont fa M, do M, sol M et ré M. De même les seules tonalités mineures sont ré m, la m, mi m et si m. Sachant que les 4 cordes à vide du violon moderne sont accordées sur les notes sol3, ré4, la4 (440 Hz) et mi5, vous comprenez mieux pourquoi l'immense majorité des grands concertos du répertoire sont écrits dans une des 8 tonalités mentionnées (Les exceptions sont rares mais elles existent, telle le rarement joué second concerto de Schostakovitch qui est en ut dièse mineur). Vous pouvez recommencer le raisonnement à propos du violoncelle dont les cordes à vides sont également accordées selon le cycle des quintes réelles, do2, sol2, ré3 et la3 (220 Hz) : les tonalités "confortables" sont cette fois : sib M, fa M, do M, sol M, sol m, ré m, la m et mi m. Le raisonnement ne tient pas pour le piano qui est accordé au tempérament égal (Cf infra) : rien ne s'oppose à ce qu'il existe des concertos pour piano dans une tonalité quelconque.
Un second élagage est rendu possible par le fait que les notes se regroupent sur le cercle par deux (ou par trois) autour des sommets d'un dodécagone régulier. Au voisinage de chaque sommet, les notes ne sont distantes que d'un comma pythagoricien (on pourrait les appeler enharmoniques, cf supra), d'où l'idée de n'en retenir qu'une seule par sommet. Cela se fait très simplement en sélectionnant 12 notes consécutives dans la liste précédente : on constate que, quel que soit le point de départ qu'on se donne, chaque note est bien voisine d'un sommet différent du dodécagone. Il existe, en théorie, 10 gammes de 12 notes, de ce type, qu'on pourrait également qualifier d'enharmoniques car elles ne diffèrent que par le choix de notes enharmoniques. On n'en conserve habituellement que 6, précisément celles qui contiennent les notes naturelles (do, ré, mi, fa, sol, la , si), que l'on réarrange comme suit, dans l'ordre des fréquences croissantes :
| do | réb | ré | mib | mi | fa | solb | sol | lab | la | sib | si | (do) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| td | tc | td | tc | td | td | tc | td | tc | td | tc | td | |||||||||||||
| do | réb | ré | mib | mi | fa | fa# | sol | lab | la | sib | si | (do) | ||||||||||||
| td | tc | td | tc | td | tc | td | td | tc | td | tc | td | |||||||||||||
| do | do# | ré | mib | mi | fa | fa# | sol | lab | la | sib | si | (do) | ||||||||||||
| tc | td | td | tc | td | tc | td | td | tc | td | tc | td | |||||||||||||
| do | do# | ré | mib | mi | fa | fa# | sol | sol# | la | sib | si | (do) | ||||||||||||
| tc | td | td | tc | td | tc | td | tc | td | td | tc | td | |||||||||||||
| do | do# | ré | ré# | mi | fa | fa# | sol | sol# | la | sib | si | (do) | ||||||||||||
| tc | td | tc | td | td | tc | td | tc | td | td | tc | td | |||||||||||||
| do | do# | ré | ré# | mi | fa | fa# | sol | sol# | la | la# | si | (do) | ||||||||||||
| tc | td | tc | td | td | tc | td | tc | td | tc | td | td |
Note. Les variantes enharmoniques des première et sixième lignes sont aisées, ne contenant que des bémols ou des dièses. La variante de la troisième ligne est celle adoptée par J-S Bach pour l'ordre des tonalités majeures dans le Livre I des 24 Préludes et Fugues du Clavier bien tempéré (do, do#, ré, mib, mi, fa, fa#, sol, lab, la, sib, si). Un tel choix enharmonique n'a plus de raison d'être avec l'adoption du tempérament égal qui confond un do# et un réb. Dans son hommage à Bach, Dimitri Schostakovitch a ordonné ses 24 Préludes et Fugues, opus 87, dans l'ordre des quintes ascendantes, de réb à fa# pour les tonalités majeures et de mib à sol# pour les tonalités mineures. Chopin ne procédera pas autrement dans son recueil de 24 Préludes, opus 28.
8) L'imbroglio des octaves, des quintes et des tierces
Il semblerait que nous ayons bien progressé dans la construction d'une gamme acceptable mais le modèle pythagoricien souffre encore de deux défauts majeurs qu'il faut corriger :
- Une partition de l'octave de base en 12 intervalles plus ou moins égaux semble se dégager mais le problème de l'étendre aux octaves voisines demeure entier. L'idée, qui paraît naturelle, de reproduire la succession des 12 notes une octave plus haut, en doublant simplement les fréquences de chacune, ne fonctionne malheureusement pas car le rapport de quinte 3/2 ne serait pas respecté d'une octave à l'autre, ce qui est inconcevable dans un modèle qui fait tout pour préserver les quintes justes. Pour que cela fonctionne, il faudrait que lorsqu'on empile 12 quintes, on retombe sur la note de départ, auquel cas on aurait effectivement réussi à partitionner harmonieusement l'octave considérée (et dès lors, toutes les autres). Cela n'arrive malheureusement jamais car l'équation, (3/2)N = 2k, n'a pas de solution entière en N et k. L'impossibilité apparaît mieux lorsqu'on réécrit l'équation sous la forme équivalente, 3N = 2N+k : une puissance de 3, nécessairement impaire, n'est jamais égale à une puissance de 2, évidemment paire. L'équation est cependant "presque" satisfaite pour les valeurs, N=12 et k=7. C'est bien pour cela qu'une partition de l'octave en 12 intervalles semble si tentante mais le fait demeure que "12 quintes excèdent 7 octaves" même si c'est de fort peu, un comma pythagoricien, P = 1200 ℓg(312/219) = 23.46 (cents), la figure suivante le rappelle.
- Même sans sortir de l'octave de base, on a cet autre problème que le modèle pythagoricien ne respecte pas la pureté de l'intervalle de tierce, cela apparaît également sur cette figure. C'est la conséquence d'une autre incompatibilité de nature arithmétique, entre la quinte et la tierce. Cette fois c'est l'équation, (3/2)N = 2k (5/4)j, qui ne possède pas de solutions entières en N, k et j. Il existe, par bonheur, une solution approchée, N=4, k=2 et j=1, que l'on traduit habituellement en disant que "4 quintes successives excèdent de fort peu une tierce majeure située deux octaves plus haut". L'écart s'élève, cette fois, à un comma syntonique, Z = 1200 ℓg(81/80) = 21.506 (cents).
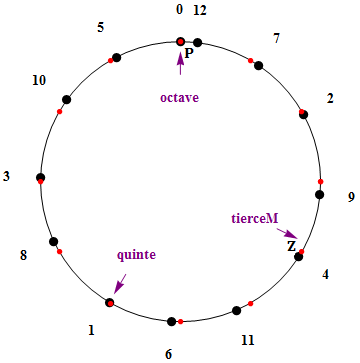
Dans les deux cas, c'est déjà ça, les quintes s'avèrent trop longues. Evidemment, il ne faut pas trop demander : pour refermer l'octave sur le cycle des quintes il faudrait diminuer, en moyenne, 12 quintes de P soit environ P/12 = 1.955 (cents), par quinte, tandis que pour rendre les tierces pures, il faudrait diminuer, en moyenne, 4 quintes de Z, soit Z/4 = 5.38 (cents), par quinte, ce qui est nettement plus ! Vous étiez prévenus, un compromis s'avère nécessaire, c'est tout le problème du (choix d'un bon) tempérament.
Une gamme naturelle ?
Le modèle pythagoricien n'assure, par construction, que la pureté de l'intervalle de quinte ascendante. Il ne se préoccupe absolument pas de la justesse des autres intervalles, par exemple des tierces (majeures, 5/4), fausses d'un comma syntonique, Z.
Cependant le travail qu'on a fait, en empilant des quintes justes, ne pourrait-on pas aussi le faire pour les tierces ? C'est en effet possible mais au prix d'une complication inévitable : passer de une à deux dimensions.
Rappelons l'alignement des quintes, toutes espacées d'un intervalle, Q = 701.955 (cents) :
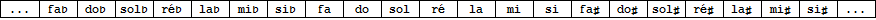
On étend le modèle aux tierces (majeures) en propageant le tableau dans la direction verticale du plan. Au départ de n'importe quelle note, toute progression horizontale (de gauche à droite) fait monter d'une quinte (3/2) et toute progression verticale (de haut en bas) fait monter d'une tierce majeure (5/4), toujours ramenées à l'octave de base. Le tableau résultant est infini et la figure ci-dessous ne fait que l'ébaucher, au départ de la note do, prise comme référence.
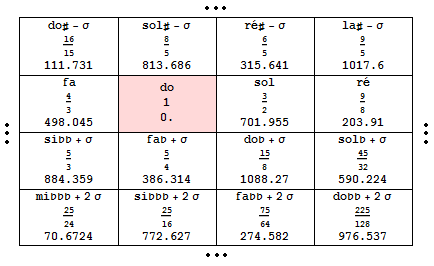
Le point délicat concerne l'appellation des notes. Il devrait être clair que les notes présentes sur la ligne du "do" doivent recevoir un nom conforme au cycle des quintes mais que pour toutes les autres, il faut respecter une nomenclature cohérente. Il se démontre que chaque note se situe dans le voisinage immédiat, c'est-à-dire à quelques schismas (σ = P - Z = 1.955 cents) près, d'une note située quelque part dans le cycle des quintes primitif (de la ligne du do). Le tableau ci-dessus montre quelques exemples.
Note technique. Bien que ce ne soit pas le lieu d'une savante démonstration, indiquons néanmoins le principe de cette nomenclature, souvent maltraitée dans la littérature. On numérote comme suit les lignes et les colonnes de ce tableau infini : la ligne et la colonne qui se croisent sur la note "do" portent chacune le n°0. Les lignes supérieures et les colonnes situées à gauche sont numérotées en reculant, -1, -2, etc, tandis que les lignes inférieures et les colonnes situées à droite sont numérotées en progressant, +1, +2, etc. Les coordonnées (u, v) de n'importe quelle note sont à présent définies par les numéros de la ligne et de la colonne qui se croisent sur elle. Par exemple, la note située dans le coin inférieur gauche possède les coordonnées, u = -1, et v = 2. On passe du "do" de référence à cette note en empilant u quintes (rapport 3/2, attention si u est négatif, la quinte est descendante, de rapport 2/3) et v tierces (rapport 5/4, attention si v est négatif, la tierce est descendante, de rapport 4/5). On calcule que la note la plus proche (à v σ près) dans le cycle des quintes est caractérisée par le doublet (m = Mod[1+u-8v,7], n = Floor[(1+u-8v)/7]), où l'entier, m, désigne la note selon le code, fa (m=0), do (m=1), sol (m=2), ré (m=3), la (m=4), mi (m=5) et si (m=6), et où l'entier relatif, n, indique le nombre d'altérations (-n bémols si n est négatif et n dièses s'il est positif). Dans l'exemple du coin inférieur gauche, u = -1, et v = 2, on trouve : m = 5 et n = -3, donc la note correspondante est située 2σ au-dessus du mibbb (Rappels scolaires : Mod[a,b] désigne le reste de la division de l'entier a par l'entier b et Floor[x] désigne l'entier immédiatement inférieur ou égal à x).
Cette description compliquée suffit à montrer que l'extension rigoureuse de ce tableau théoriquement infini le rend quasiment inutilisable. Il constitue cependant, mais dans une version radicalement simplifiée, le principe de base de la gamme naturelle développée par Gioseffo Zarlino (1517-1590). La simplification consiste à ignorer les enharmonies et les petits schismas correcteurs. On obtient dès lors le modèle suivant.
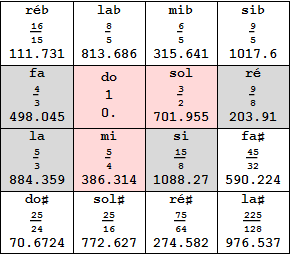
L'octave y est partitionnée en intervalles prédéfinis, fixant comme suit les fréquences relatives des notes : f0 {1 (do), 9/8 (ré), 5/4 (mi), 4/3 (fa), 3/2 (sol), 5/3 (la), 15/8 (si), 2 (do)}. Ce choix est dicté par le souci de reproduire par trois fois l'accord parfait (majeur), composé d'une note de base, de sa tierce (majeure) et de sa quinte, soit les rapports {1, 5/4, 3/2}; on a bien les accords parfaits, do-mi-sol, sol-si-ré et fa-la-do, révisez vos fractions ! En particulier, on vérifie sans peine que la tierce majeure, 5/4, est la moyenne arithmétique entre les extrêmes, 5/4 = (1+3/2)/2. Mentionnons qu'il existe également un accord parfait mineur correspondant aux rapports {1, 6/5, 3/2} où intervient la tierce mineure, de rapport 6/5, moyenne harmonique entre les mêmes extrêmes, 6/5 = 2x1x3/2/(1+3/2). Ci-contre, les 7 notes naturelles ont été ombrées et le motif de l'accord parfait majeur (trois fois répétable) a été mis en évidence, en rose. Il reste alors à compléter par les notes altérées afin que la partition de l'octave soit harmonieuse.
Cette gamme dont l'origine remonterait à Aristoxène (né vers -352) est basée non plus sur l'obsession arithmétique, typique de la philosophie pythagoricienne, mais sur le respect de l'harmonie acoustique qu'assure l'accord parfait.
Ce réseau tonal pourrait à la rigueur être reporté sur le cercle d'octave mais le résultat serait fort peu lisible du fait de l'incommensurabilité entre les intervalles de quinte et de tierce. On observerait une accumulation pseudo périodique de notes, difficile à débrouiller. Topologiquement, la structure correcte est celle d'un tore (tridimensionnel) où le cycle des quintes est parcouru hélicoïdalement (donc sans se refermer, il faudrait le tempérament égal pour que cela se produise et ce n'est évidemment pas le but) selon les arcs de grands cercles et les tierces selon les arcs de petits cercles.
A diapason égal, les fréquences des notes zarliniennes ne coïncident évidemment pas exactement avec celles du modèle pythagoricien. Les intervalles ont tendance à se multiplier, c'est le prix qu'on paye pour la justesse des tierces :
- Il existe à présent deux sortes de tons, le long (9/8, 203.91 cents) pour les intervalles do-ré, fa-sol et la-si et le court (10/9, 182.404 cents) pour les intervalles ré-mi et sol-la, la différence étant le comma syntonique, Z.
- De même, il existe à présent trois sortes de demi-tons, le diatonique (16/15, 111.731 cents) pour les intervalles mi-fa et si-do, le chromatique long (135/128, 92.178 cents) pour les intervalles fa-fa#, la-la# et réb-ré et le chromatique court (25/24, 70.672 cents) pour les intervalles do-do#, ré-ré#, sol-sol#, mib-mi, lab-la et sib-si. Les demi-tons chromatiques sont à nouveau distincts d'un comma syntonique, tout cela est inscrit dans le tableau précédent. A noter que rien que dans l'intervalle, do-ré, les altérations se succèdent dans l'ordre inverse de ce qui se passe en mode pythagoricien : do-do#-réb-ré au lieu de do-réb-do#-ré. L'intervalle do#-réb n'est pas petit, mesurant 41 cents soit un peu moins que deux commas.
Cette démultiplication des intervalles est, en fait, incompatible avec le principe de la construction d'une gamme stable convenant à un instrument à son fixe. Un tel instrument requiert, en effet, autant de systèmes oscillants autonomes (par exemple, des cordes sur un clavecin ou un piano) que de notes distinctes à émettre, d'où les facteurs d'instruments protesteraient avec raison. On a pourtant tenté de construire des claviers spéciaux adaptés à la gamme de Zarlino, par exemple à doubles feintes pour jouer différemment les altérations voisines, ou, plus compliqué encore, des claviers transpositeurs mobiles mais l'accumulation des difficultés a fait abandonner le projet. La gamme naturelle n'a pourtant pas disparu pour autant, les voix non accompagnées ayant tendance à respecter les intervalles consonants purs.
Revenus de l'utopie zarlinienne, les théoriciens ont reconsidéré le modèle pythagoricien, prêts à lâcher du lest en matière de quintes pures. Nous l'avons dit, les quintes pythagoriciennes sont trop longues pour fermer l'octave et elles sont aussi trop longues pour engendrer des tierces majeures pure. Il faut donc se résoudre à les raccourcir (les tempérer est le mot juste), toutes les quintes ou certaines d'entre elles seulement, sans trop les abîmer. On a inventé des tempéraments par dizaines et leur nombre indique bien qu'il n'en existe aucun qui soit parfait. Les présenter tous n'aurait aucun sens mais il vaut la peine d'en expliquer certains parmi les plus significatifs. Précisons que le calcul, un brin technique, des fréquences d'accordage des notes découlant du tempérament retenu ne fait pas partie de cette présentation.
Tempérer les quintes pour respecter l'octave
Douze quintes justes étant trop longues de P = 23.46 (cents) pour refermer exactement l'octave, quel(s) raccourcissement(s) peut-on envisager ? Pour y voir clair, redessinons le cercle de l'octave en positionnant différemment les notes, dans l'ordre des quintes avec un choix enharmonique, par exemple, mib, sib, fa, do, sol, ré, la, mi, si, fa#, do# et sol#. Dans cette représentation, une quinte pure est représentée par un arc mesurant 101.955 (cents) afin que 12x101.955 - 23.46 = 1200 (cents).
1) Une solution extrême : la quinte du loup
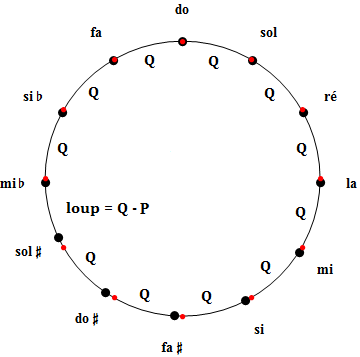
Une solution extrême consiste à raccourcir une seule quinte de l'entièreté de P, d'où les 11 autres quintes restent pures. La quinte raccourcie est inutilisable car elle sonne complètement faux, d'où son surnom de "quinte du loup (qui hurle !)". Les tonalités où cette quinte intervient sont donc proscrites, ce qui est une limitation sévère. On peut certes décider de la situer au sein d'une tonalité éloignée (de do majeur), par exemple entre sol# et mib, mais l'objection demeure que les modulations autorisées seront limitées aux tonalités voisines (de do majeur) sans quoi la quinte défectueuse est assurée de resurgir. Inutile d'ajouter que le problème des tierces fausses n'est pas réglé par cette option : à l'exception du raccourcissement dû à la quinte du loup, il n'est même pas abordé. Quintes et tierces confondues, un calcul de fausseté globale, quantité définie dans la note ci-dessous, donne une valeur de 65.31 (cents).
2) Un compromis célèbre : le tempérament Werckmeister Ⅲ (1691)
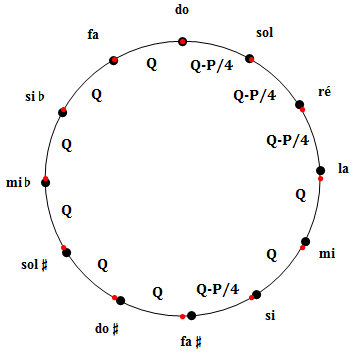
Le tempérament suivant, dû à Andreas Werckmeister (1645-1706), a connu un certain succès à l'époque baroque : il raccourcit les quintes do-sol, sol-ré, ré-la et si-fa# de P/4, qui deviennent, de ce fait, trop courtes de 5.865 (cents), un défaut acceptable pour l'oreille. Les 8 autres quintes restent pures et les tierces s'en trouvent (un peu) améliorées, surtout do-mi, qui profite de l'amputation de trois quarts de comma. Les tierces plus éloignées demeurent en l'état d'imperfection pythagoricienne. Quintes et tierces confondues, le même calcul livre une fausseté globale de 53.11 (cents).
3) Un compromis prometteur : le tempérament égal
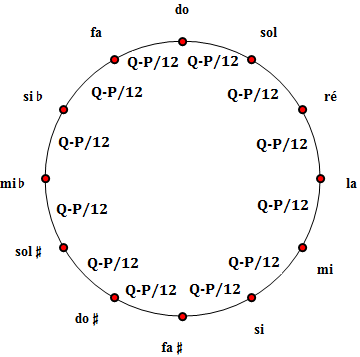
Si l'on pousse à l'extrême la logique de la répartition de P sur plusieurs quintes, on aboutit, à la limite, à un partage équitable entre les 12 quintes, qui se trouvent raccourcies chacune de 2 cents environ, ce qui est tout à fait raisonnable. Les tierces demeurent fausses à concurrence de 1200 ℓg(4/5 24/12) = 13.685 (cents) mais c'est déjà mieux que les tierces pythagoriciennes (fausses de Z = 21.506 cents, pour rappel). Les quintes raccourcies valent à présent Q-P/12 = 700 (cents), une valeur commensurable avec la quinte (1200 cents) et garantissant forcément la fermeture de l'octave. Les intervalles entre les 12 notes partitionnant l'octave valent désormais exactement 100 cents d'où les notes se placent exactement sur les points rouges qui servaient de séparateurs (Toutes les modulations sont à présent trivialement possibles). La fausseté globale est minimale dans ce tempérament, elle vaut 47.89 (cents) et il n'y a pas moyen de faire mieux.
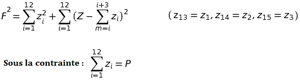
Note à l'usage des matheux. Vous trouverez dans la littérature, y compris dans celle remontant au 18ème siècle, quantité d'autres tempéraments amputant une quinte par-ci une quinte par-là, à la recherche du meilleur compromis. Ce désordre est plutôt étonnant à une époque où des mathématiciens fameux (Euler, d'Alembert, Descartes, ...) s'intéressaient à cette recherche. Ils auraient dû (sa)voir que ce problème d'optimisation quadratique ne possédait qu'une seule solution, précisément celle du tempérament égal. On s'en convainc en posant que les 12 quintes successives sont amputées (donc faussées) d'une quantité, zi (i = 1, 2, ..., 12; n'oubliez pas la contrainte que le total de ces amputations doit valoir le comma, P). Les 12 tierces s'en trouvent faussées, à leur tour, d'une quantité égale à, Z-(zi + zi+1 + zi+2 + zi+3), où l'entier i parcourt encore les valeurs de 1 à 12. On peut définir, sur cette base, une grandeur, F, qui quantifie raisonnablement la fausseté de la gamme résultante, quantité que l'on minimise par les procédés habituels de l'analyse mathématique. On trouve que le minimum de fausseté, F, est atteint lorsque tous les zi sont égaux à P/12, c'est bien le tempérament égal. Sans doute les musiciens objecteront-ils qu'une bonne oreille vaut mieux qu'un calcul aussi savant soit-il. Il n'empêche que pour cette fois ce furent les mathématiques qui finirent par avoir raison : le tempérament égal s'est progressivement imposé, à partir de 1800, non sans mal il est vrai.
La possibilité d'un tempérament égal n'avait pas échappé aux théoriciens de la Renaissance et de la période baroque (On dit même qu'elle était connue des chinois, depuis très longtemps). S'ils l'ont rejetée, dans un premier temps, c'est qu'ils étaient obsédés par la pureté des tierces.
Tempérer les quintes pour respecter les tierces
Bien qu'à ce stade toute prospection supplémentaire paraisse superflue, au motif que l'optimum mathématique ait été prouvé coïncider avec le tempérament égal, l'histoire de la musique baroque mais aussi son renouveau actuel serait incompréhensible sans faire le détour par les tempéraments inégaux, adaptés à une plus grande pureté des tierces (donc une dégradation des quintes).
4 quintes pures étant trop longues de Z = 21.506 (cents) pour fabriquer une tierce majeure pure et Z n'étant après tout pas si éloigné de P = 23.46 (cents), les théoriciens de l'époque baroque ont passé un certain temps à chercher d'autres compromis basés sur l'amputation des quintes d'une fraction de Z (au lieu de P).
1) Encore un loup !
Le tempérament qui garantit le maximum (8) de tierces pures raccourcit 11 quintes de Z/4 et il allonge la douzième, qui fatalement devient fausse, de 7Z/4 - σ = 35.682 (cents), afin de garantir la fermeture de l'octave. Ce loup peut à nouveau être déplacé dans l'intervalle éloigné sol#-mib mais les modulations dans les tons éloignés demeurent problématiques.
2) Le tempérament ordinaire ?

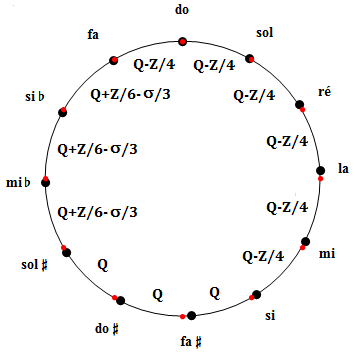
Diderot a fait mention d'un "Tempérament ordinaire" dans ses écrits et Rousseau y a également fait allusion dans son tardif Dictionnaire de Musique (1768). Il s'agirait, selon toute vraisemblance, du tempérament en usage en France vers le milieu du 18ème siècle. Etrangement, Diderot n'en a donné aucune description précise comme si le sujet était suffisamment connu de tous pour se passer des détails (mais alors à qu(o)i servait l'Encyclopédie ?). Les musicologues ont analysé la description de Rousseau, un brin obscure et même contradictoire, et ils ont fini par admettre (sans garantie !) que 6 quintes (fa-do-dol-ré-la-mi-si) devaient être amputées de Z/4, les trois suivantes demeurer pures et les trois dernières être dilatées de Z/6 - σ/3, afin de refermer l'octave. Cela est représenté dans la figure ci-dessous. Les musiciens actuels sont au moins d'accord sur un point : ce tempérament ordinaire est plaisant et jouable dans toutes les tonalités. De plus, chaque tonalité possède sa couleur propre ce qui est bien dans l'idéal baroque.

On aurait pu espérer que Rameau, notoirement impliqué dans la théorie musicale au point de lui avoir consacré trois traités successifs (1722, 1726 et 1737), nous aurait éclairé définitivement sur la nature du tempérament idéal à ses oreilles mais il n'en est rien. D'un exposé à l'autre, il n'a cessé de se contredire pour finir par recommander du bout des lèvres le tempérament égal en pleine ascension dans l'air du temps. Le raffinement harmonique de sa musique est pourtant en parfaite contradiction avec cette recommandation et cela ne fait pas l'affaire des interprètes actuels qui en sont toujours à se demander quel tempérament ils doivent utiliser quand ils jouent sa musique. William Christie, engagé à Glyndebourne pour une représentation d'Hippolyte et Aricie, en 2013, a adopté un tempérament basé sur 7 quintes amputées de P/4, 2 quintes exactes, une quinte amputée de P/6 et deux quintes dilatées de 11P/24 (des demi-loups en quelque sorte, cf ce diagramme, proposé par la CBH Technical Library) mais tout le monde n'approuve pas qu'il s'agisse réellement du tempérament préféré du compositeur. La seule chose qui est sûre, c'est qu'on ne veut plus entendre jouer Rameau au tempérament égal (et sur instruments modernes) comme cela se pratiquait dans les années 1950 (On ne s'en plaignait même pas, tout heureux d'entendre un peu de musique de cet illustre musicien !).
3) Le tempérament de J-S Bach ?
Une autre polémique divise les musicologues concernant la diffusion du tempérament ordinaire en-dehors des frontières de l'Hexagone. Nul ne sait avec exactitude comment étaient accordés les instruments joués par J-S Bach ni ne connaît le tempérament souhaité par le compositeur dans son oeuvre didactique et magistrale "Das Wohltemperierte Klavier", regroupant 24 préludes et Fugues dans tous les demi-tons majeurs et mineurs de la gamme chromatique (Le premier cahier date de 1722 et le second, identique dans son esprit, date de 1744).

Bien que le principe du tempérament égal ait été connu à l'époque de Bach, celui-ci n'était nullement en usage. Avant Bach, il était courant de renoncer aux tonalités trop chargées en altérations afin de préserver (les nuances de) celles qui étaient jouables. "Bien" tempéré ne signifie donc pas "également" tempéré mais "convenablement" tempéré, de telle manière que les modulations dans les 24 tonalités majeures et mineures soient effectivement possibles.
Le 19ème siècle a vécu avec cette erreur que Bach pensait au tempérament égal mais si l'on y réfléchit un instant, cela n'aurait eu aucun sens que Bach passe son temps à écrire une pièce en do majeur puis une autre en do# majeur quand celle-ci sonnerait simplement comme la précédente, un demi-ton plus haut. Ce que Bach avait en tête était, sans doute, un tempérament inégal quoique jouable dans toutes les tonalités sans réaccordage de l'instrument. En particulier, chaque prélude devait conserver sa couleur particulière, conformément à l'esprit baroque. Quand on comprend ce raisonnement il ne reste plus qu'à en tirer la conclusion inéluctable : le Clavier bien tempéré "doit" être joué sur un (bon !) clavecin convenablement accordé. Réécoutez Kenneth Gilbert, c'est tout à fait convaincant. Datée de 1983, la très documentée pochette de son quadruple CD mentionne l'incertitude planant encore et toujours sur le tempérament voulu par Bach mais, inexplicablement, elle ne dit rien du tempérament qu'il a réellement utilisé comme interprète. Cela dit, on peut faire ce reproche à la plupart des enregistrements pour clavecin, ce qui devrait désormais vous agacer.
Sans y avoir assez réfléchi, j'ai longtemps été de l'avis de ceux qui pensaient que si Bach avait disposé du piano moderne, il aurait écrit son oeuvre pour cet instrument mais c'est un contresens manifeste. Cela dit, rien n'empêche que vous conserviez précieusement la version pianistique qui vous tient à coeur (Andras Schiff ?) !
Reste qu'à ce stade, on ne connait toujours pas le tempérament sous-entendu par Bach. Le musicologue, Bradley Lehman (site à visiter !), a publié une thèse, en 2005, tendant à démontrer que la clé de l'énigme se trouvait peut-être dans la succession des volutes, présumées cryptées et gribouillées par Bach en haut de la page de garde du manuscrit de son premier cahier. Vous en trouverez un agrandissement ci-dessous, renversé pour les besoins de la démonstration à venir.

Personne aujourd'hui ne pense que ces arabesques étaient là pour faire joli ni qu'un enfant les a griffonnées à l'insu de son illustre père. Le compositeur cryptait volontiers quelques messages numérologiques dans ses partitions (cf l'exposé de Gilles Cantagrel, Symbolique et Rhétorique chez J-S Bach); n'aurait-il pas utilisé le procédé dans un autre registre ? Certains le pensent et Lehman croit pouvoir affirmer que ce rébus indique le tempérament souhaité. C'est d'autant plus crédible que dans le texte de présentation qui complète la page de garde de son recueil, Bach précise son intention d'inciter les clavecinistes à faire la démonstration qu'il est possible de jouer dans tous les tons majeurs et mineurs. Reste à décrypter la devinette, si devinette il y a.
Quelques observations sautent aux yeux lorsqu'on regarde la fresque, de gauche à droite :
- 12 volutes se suivent : la première est déformée et fait l'objet d'interprétations divergentes (cf infra); les 5 qui suivent sont toutes à double boucles, suivies par 3 volutes dépourvues de boucle et enfin par 3 volutes à boucle simple.
- Une lettre, C, apparaît clairement, entre les volutes 2 et 3; elle n'est renversée que parce que on a retourné la figure. Cette lettre évoque sans doute la place du do sur le cycle des quintes tel que nous le représentons (C'est pour cela que la figure est inversée).
- Quelques lignes incurvées supplémentaires sont présentes dont l'interprétation s'avère sujette à caution, à supposer qu'elles soient réellement interprétables.
Les 12 volutes réparties en trois classes font irrésistiblement penser aux 12 quintes, tempérées de trois façons différentes. Je n'ai entendu personne mettre en doute la pertinence de la thèse du rébus, par contre les interprétations divergent :
- Lehman pense que la première boucle échappe à tout codage : elle ne fait que signifier, qu'une fois fixés les tempéraments des 11 dernières quintes, la première ne peut qu'être ajustée afin que l'octave se referme. Sa thèse est que les 5 quintes à doubles boucles (fa-do-sol-ré-la-mi) sont amputées de P/6, les 3 quintes dépourvues de boucle (mi-si-fa#-do#) demeurent intactes et les 3 quintes à boucle simple (do#-sol#-mib-sib) sont amputées de P/12 (Deux fois moins de boucles, tempérament réduit de moitié !). De cette façon, la quinte restante, sib-fa, est dilatée de P/12 afin que les 12 quintes reconstituent l'octave. Ce tempérament est jouable dans tous les tons où il présente les différences subtiles attendues.
- Le claveciniste, Dominic Eckersley, a contesté l'interprétation de Lehman dans un article tout aussi documenté et argumenté (The Rosetta revisited, 2012). Eckersley est d'avis que la première volute fait partie intégrante d'un premier sous-ensemble de 6 quintes et qu'elle correspond à une amputation (zarlinienne et non pythagoricienne) de Z/4 par quinte. Les 3 quintes suivantes restant pures (là tout le monde est d'accord), il en déduit que les 3 dernières quintes doivent subir une légère dilatation de (Z/6 - σ/3) chacune. Si vous suivez, vous réalisez que ce n'est rien d'autre que le tempérament ordinaire français ! Cela n'aurait rien de choquant : Bach appréciait les compétences développées par l'école française de clavecin (cf cette chronique) et il a très bien pu considérer que ce tempérament ordinaire convenait mieux que la cohorte des tempéraments germaniques dont vous trouverez une description ici.
- Le musicologue Georges Kan a étendu au texte écrit, singulièrement aux titres, l'analyse de la graphie tarabiscotée utilisée par Bach dans la présentation de la page de garde de son recueil. Il est d'avis que rien n'y est laissé au hasard mais qu'au contraire un message s'y trouve crypté, qui ne peut qu'être d'interprétation sacrée, la foi chez Bach étant omniprésente. Vous trouverez en annexe (La Genèse de Bach, 2018) l'exposé complet de cette recherche.
4) Le tempérament de Vallotti
L'étude des tempéraments n'est plus d'actualité depuis qu'on a adopté le tempérament égal. Seuls les baroqueux continuent de s'y intéresser, par la force des choses. Un tempérament commode car facile à implémenter est celui de Francesco Antonio Vallotti : il diminue les 6 quintes allant de fa à si de Z/6 et dilate la quinte sol#-mib du schisma résiduel, les autres quintes demeurant pures. Cela dit les querelles d'écoles ne se sont pas tues et les interprètes peuvent parfaitement hésiter avant d'opter pour un tempérament ! Au clavecin, il n'est d'ailleurs pas rare que l'instrument soit réaccordé à la pause d'un concert afin de mieux se prêter au répertoire de la deuxième partie.
Aujourd'hui, rien n'empêche de concevoir un tempérament original. Le facteur, Anthony Sidey, a pris cette initiative, relayée par Blandine Verlet dans un enregistrement récent de pièces choisies de François Couperin.
Retour au tempérament égal
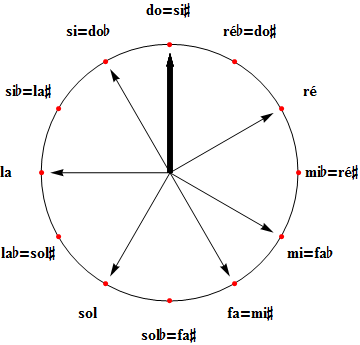
Le tempérament égal revient à diviser l'octave en douze intervalles rigoureusement égaux à 100 cents chacun (demi-tons tempérés). Dans ce système, le cycle des notes se répète avec une périodicité parfaite d'où la transposition devient un jeu d'enfant : il suffit de décaler les intervalles du pas constant désiré et on est certain de retomber sur une note de la gamme ainsi définie. On note que, par rapport au cycle pythagoricien, les notes enharmoniques ont purement et simplement fusionné. Vous trouverez ci-dessous le tableau des fréquences des notes en tempérament égal et au diapason moderne (la4 = 440 Hz). Ce tableau ne convient pas pour la musique ancienne, qui opte pour un tempérament inégal et pour un diapason généralement situé (à peu près) un demi-ton plus bas, à 415 Hz.
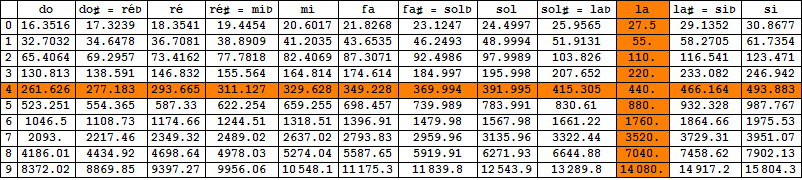
Le piano est, par excellence, l'instrument qui a adopté le tempérament égal, à quelques subtilités près qui concernent les registres extrêmes où les octaves sont légèrement étirées. Cette facilité s'est d'autant mieux imposée que l'intensité du son produit masque les imperfections harmoniques. Le tempérament égal est un non-sens au clavecin car il s'oppose au raffinement sonore de l'instrument; il est pourtant fréquent, en particulier au concert, lorsqu'on ne peut se permettre un réaccordage en fonction de la tonalité des pièces programmées. En enregistrement de studio, il ne se justifie absolument pas. Les cordes du violon moderne sont habituellement accordées selon l'ordre des quintes, sol, ré, la et mi, pythagoriciennes en théorie mais égales en pratique car un violon joue rarement seul. La situation du violon baroque peut s'avérer (nettement) plus compliquée, certaines partitions exigeant des accordages différents (par quartes, tierces, etc, c'est la Scordatura). Les célèbres (et difficultueuses !) Sonates du Rosaire de Heinrich Ignaz Franz Biber (1644-1704) sont dans ce cas.
L'adoption du tempérament égal simplifie incontestablement la tâche des pianistes mais le (modeste) prix à payer, c'est qu'à l'exception de l'octave, plus aucun intervalle ne sonne rigoureusement juste. Les rapports de fréquences des notes, tous du type, 2k/12 (k entier), sont devenus irrationnels, bien loin de l'idéal pythagoricien des fractions simples : si les quintes et les quartes sont pures à 1.95 cents près, ce qui est excellent, les tierces majeures et les sixtes mineures ne le sont qu'à 13.686 cents et c'est encore pire pour les tierces mineures et les sixtes majeures, "pures" à 15.641 cents près seulement. De plus, le tempérament égal gomme les différences de couleurs entre les tonalités d'où c'est devenu un abus de prétendre qu'en musique classico-romantique, l'ut majeur est martial et le fa majeur furieux et emporté : les deux sonnent pareillement à une quinte de distance.
Aucun musicien de l'époque baroque naissante n'aurait souscrit au tempérament égal. Pourtant, avec le temps, en particulier le développement de la musique pour ensembles instrumentaux, les musiciens ont compris que les problèmes de modulation allaient vite devenir insolubles, ce qui ouvrait inexorablement la porte au tempérament égal. Celui-ci n'a cependant été complètement effectif que vers 1850 (Beethoven était mort depuis 23 ans !), le temps que les accordeurs se mettent ... d'accord. Parmi tous les tempéraments envisageables, il est, en effet, resté longtemps un des plus difficile à régler, précisément par ce qu'aucun de ses intervalles n'est rigoureusement exact : l'accordage par l'ouïe, traditionnellement basé sur l'écoute des battements, est restée problématique jusqu'à l'avènement du diapason électronique. En 1940, Llewellyn Lloyd s'autorisait encore à publier un article (The Myth of Equal Temperament”, Music & Letters (1940b), 347-361), prétendant que le tempérament égal demeurait un mythe impossible à atteindre. En particulier, les chorales a capella n'adhèrent pas spontanément à un système contraire à l'intuition du chanter juste.
Il faut s'en faire une raison, le tempérament égal est une hérésie musicale à laquelle nos oreilles se sont parfaitement habituées. Seuls certains pavillons fragiles (mais expérimentés !) en souffr(ai)ent encore, telles celles du grand baroqueux, Nikolaus Harnoncourt, qui ne parvenait pas à s'y faire. Alors oubliées les conséquences du tempérament inégal ? Pas du tout et les apprentis musiciens en savent quelque chose qui doivent apprendre une orthographe musicale précisément héritée du tempérament inégal et bien peu en rapport avec la simplicité qu'aurait dû leur promettre une gamme "enfin rationnalisée". Mais ceci est une autre histoire dont un chapitre, au moins, relatif aux excès de la notation, fera l'objet d'une prochaine présentation.
Note ajoutée en 2020. Un opuscule recommandable vient de paraître aux éditions Aedam Musicae, sous le titre "Clavier bien tempéré et Justesse numérique". L'auteur, Florent Ploquin, y retrace l'histoire de l'accordage des instruments à clavier, en particulier la quête sans fin d'un tempérament idéal jusqu'à l'adoption plus ou moins contrainte et forcée du tempérament égal. Le dernier chapitre, particulièrement original, aborde les résultats des recherches acoustiques récentes appliquées au domaine des claviers numériques.
Et la musique dans tout cela ?
Le moment est venu d'illustrer les notions évoquées par quelques musiques d'époque.
C'est en France, pendant l'ère médiévale, que la polyphonie savante a fait ses premiers pas. Cela s'est fait très progressivement et jusque vers l'an 1000, on ne dépassait pas le stade de la diaphonie (ou organum parallèle) : la mélodie du plain-chant grégorien (vox principalis, aiguë) était simplement doublée en notes parallèles situées une quinte (ou une quarte) plus bas (vox organa), l'idéal pythagoricien était respecté. Des variantes multiples ont très vite prospéré (déchant, renversements, mouvements contraires, etc) mais ce n'est pas le lieu de les commenter.
Un siècle plus tard, en Angleterre, cette technique a été étendue à la tierce (et à son complément, la sixte), c'est le procédé plus rugueux du gymel. On attribue généralement cette initiative à John Dunstable (1390-1453). L'oeuvre de ce musicien a malheureusement été largement détruite lors du saccage des monastères à l'époque de la Réforme (1538). Nous n'en avons conservé que quelques copies passées à temps sur le continent, où elles ont influencé durablement la génération de Guillaume Dufay. La tierce a alors acquis son statut définitif de consonance imparfaite. Voici une illustration de cette "Contenance angloise" (sic), "Thomas Gemma Cantuarie" (Auteur anonyme de 14ème siècle), dans deux interprétations radicalement différentes, dues aux Ensembles Hilliard et De Caelis. La première regarde logiquement vers le Moyen-Age finissant tandis que l'autre emprunte abusivement au courant de la Renaissance (cf infra).
Avec le temps (et le commerce des épices ?), les oreilles continentales se sont habituées aux frottements créés par ces tierces un peu fausses, jusqu'à y prendre goût. L'idée a dès lors germé de les purifier, ce qui réclamait soit des aménagements dans le modèle pythagoricien, c'était la technique du tempérament, soit une refonte complète de la théorie, c'était l'idéal de la gamme naturelle. La Renaissance tardive a largement cultivé les tierces exactes dans un ensemble de pièces vocales a capella conformes à l'idéal de pureté de la Contre-Réforme. Les choeurs non accompagnés se sont sentis à l'aise dans cette justesse intrinsèque même si les objections ne manquaient pas : comme l'a noté Jacques Chailley, les accords zarliniens se satisfont de leur propre justesse sans chercher ailleurs leur résolution. Il en résulte un chant lisse, certes impeccable mais lassant sur le long terme et peu prometteur pour (la musique de) l'avenir (Giovanni Pierluigi da Palestrina (1525-1594) : Sicut cervus et Sitivit anima mea et Missa brevis; Tomas Luis de Victoria (1548-1611) : Missa Salve Regina). Avec ses tierces légèrement trop longues (de Z/4), le modèle pythagoricien crée davantage de tensions qui demandent à être résolues. Il en résulte un discours dynamique quand le discours zarlinien demeure nettement statique. Entre les deux, le tempérament égal saura se frayer un chemin, représentant un compromis fonctionnel qui n'a que le défaut d'abolir notre instinct de justesse.
Le tempérament inégal, cultivé par l'école française de clavecin (François Couperin (1668-1733) : La Ménetou) - on pourrait y ajouter le répertoire pour orgue - fut encore célébré par Rousseau, 50 ans plus tard. Les musiciens baroques, férus de pittoresque, se sont délectés des atmosphères différentes propres à chaque tonalité. Marc-Antoine Charpentier (1636-1704) avait même tenté un inventaire des caractères par tonalités (cf ce lien : Muse baroque), que Rameau n'approuva que dans les cas flagrants.
Le tempérament inégal n'a pas pas passé le cap de la Révolution française. Les clavecins, victimes d'un Ordre nouveau, ont fait place aux piano(forte) plus sonores et moins regardants quant aux nuances infinies que les auditeurs percevaient, de toute façon, de moins en moins. L'histoire allait dans le sens d'une lente appropriation d'intervalles de moins en moins confortables, comptant sur la complicité d'auditeurs tolérants et surtout curieux.
Aux époques classique et romantique, les oreilles se sont complètement habituées au tempérament égal, préférant se concentrer sur les possibilités infinies qu'offrait le jeu des modulations. Les quintes (Joseph Haydn : Célèbres deux premières mesures du Quatuor opus 76 n°2) et autres accords parfaits ont prospéré jusque dans des oeuvres tardives et célèbres : les fameuses premières mesures du poème symphonique Also sprach Zarathoustra (1896) de Richard Strauss en proposent un condensé éloquent.
L'époque moderne a tellement brouillé les pistes (et les intervalles !) qu'elle n'est plus guère susceptible d'illustrations pertinentes : les quintes et les tierces subsistent évidemment mais elles côtoient désormais des intervalles de plus en plus larges, frisant l'extravagance quand ils s'adressent à la voix. Dans ses mémoires, le grand chef russe Guennadi Rojdestvenski raconte que, tant à Saint-Pétersbourg qu'à Moscou, les visites d'inspection des travaux de fins d'étude, par la Commission du Prolektikut, déclenchait un vent de panique chez les élèves : tous, armés d'une gomme ou d'un grattoir, remplaçaient (provisoirement !) les intervalles dissonants par une quinte par-ci, une quarte par-là.
Le cas posé par la seconde école de Vienne est différent. Le dodécaphonisme a clairement adopté le tempérament égal non par commodité mais par nécessité quasiment logique. Cela ne l'a pas empêché de connaître toutes sortes de variantes dissidentes où la consonance n'était pas forcément absente. Si celle-ci fut nettement évitée par Webern, tel ne fut pas le cas d'Arnold Schönberg ni d'Alban Berg (Concerto pour violon), pour s'en tenir à deux acteurs essentiels de cette école. Que l'uniformisation de la gamme à 12 sons n'ait pas débouché sur une refonte simplificatrice de la notation musicale est un mystère sur lequel je reviendrai prochainement.
Enfin et provisoirement, les 40 dernières années ont connu le retour en force de la tonalité et de son extension, la modalité, pour le plus grand plaisir de ceux qui ne se lassent pas de ces quintes, quartes, tierces et autres sixtes qui nous ont tant occupés (Philip Glass : Dance IX et sa caricature, Music in Fifths, une réaction contre "l'interdiction" enseignée dans tous les conservatoires d'(ab)user de ces mouvements en quintes parallèles qu'un 20ème siècle blasé a jugées tout juste dignes de l'an 1000).