Faits divers
Acoustiques musicales
Sommaire
[ afficher ]- Le son comme onde de pression
- Classification des instruments de musique
- Le cas d'école du diapason
- Vibrations de la corde idéale
- Le violon et la corde idéale
- Vibrations de la lame épaisse
- Quelques lamellophones
- Vibrations de la corde raide
- Le piano fait de la corde raide
- La perception du son
- Mirages et merveilles de l'électronique
Musique et (acoustique) physique entretiennent à l'évidence des rapports étroits, en particulier au niveau de l'étude des instruments de musique (l'organologie). Cependant si la physique explique bien la façon dont les sons sont émis et transportés, elle est fondamentalement incapable d'analyser correctement la manière dont ils sont reçus et codés par l'oreille humaine puis interprétés par le cerveau. Au 19ème siècle, un physicien et physiologiste réputé, Hermann Ludwig von Helmholtz (1821-1894), a bien tenté d'intégrer les approches physique, biologique et psychoacoustique en un tout cohérent mais ses travaux n'ont pas été couronnés du succès espéré. C'était inévitable dès l'instant où la détection des signaux sonores par l'oreille ne présente pas le caractère objectif qu'on prête aux instruments de laboratoire :
- Le physicien Helmholtz savait assez de théorie physique pour expliquer complètement les modes de vibration spontanée des systèmes élastiques (cordes, lames, membranes, etc) lorsqu'on les excite. Les calculs établissent que les fréquences propres de ces modes sont d'autant plus basses que les dimensions et les masses des systèmes sont élevées et que les contraintes mécaniques (tension, raideur, etc) sont faibles (Cf infra). Par ailleurs, il savait aussi que si l'on soumet l'un de ces systèmes, provisoirement au repos, à une vibration extérieure de fréquence donnée, il entre en vibration forcée, d'autant plus intense que la fréquence excitatrice est proche de l'une de ses fréquences propres. Lorsque la coïncidence a lieu, on dit que le système entre en résonance. Si l'on s'éloigne de la résonance, la vibration forcée demeure mais elle est d'intensité nettement moindre. La différence entre vibration spontanée et forcée est essentielle pour la suite : une membrane de grande timbale usuelle, de surface = 0.528 m2, descend en fréquence jusqu'au do2 (65.4 Hz) mais pas plus bas. Lorsque le son qu'elle émet atteint un tympan humain, de section = 60 mm2 (8800 fois plus petite !), il devrait être clair que celui-ci ne vibrera que très faiblement (avec une amplitude généralement inférieure au micromètre) car on se situe très loin de la résonance. Dans ces conditions, l'oreille interne doit déployer des trésors d'inventivité, en matière d'amplification, pour assurer l'audition.
- Le physiologiste Helmholtz a cru trouver dans la résonance la clé du mécanisme de l'audition au niveau de l'oreille interne. La difficile question posée était de comprendre comment celle-ci se débrouillait, en si peu d'espace, pour différencier à quelques Hz près des sons pouvant s'étaler entre 16 et 16000 Hz (soit 10 octaves !), sans parler des rapports d'intensité, entre 0 et 120 dB (soit 12 ordres décimaux !). Il connaissait assez d'anatomie pour savoir que la transduction du signal ondulatoire en signal électrique à destination du cerveau se faisait au niveau de la cochlée, plus précisément des cellules ciliées de l'organe de Corti. Se remémorant ses connaissances physiques, Helmholtz a (sup)posé que chaque cil était accordé sur une fréquence particulière et qu'il fonctionnait comme une corde entrant en résonance lorsque l'onde sonore l'atteignait. On s'est très vite rendu compte que les caractéristiques physiques des cils ne permettaient pas de se contenter de cette hypothèse. Plus récemment et de façon inattendue, les idées d'Helmholtz ont pourtant resurgi dans un cadre perfectionné comportant cependant encore des zones d'ombre (Cf infra).
Cette chronique expose et commente quelques règles de l'acoustique s'appliquant en organologie : leur importance mais aussi leurs limites à partir desquelles la physiologie de l'oreille entre inévitablement en jeu. Car il n'y a pas qu'une acoustique, d'où le titre, au pluriel.
Le son comme onde de pression
Un corps matériel qui vibre dans le vide n'y crée aucun son, il se contente de vibrer, un temps d'autant plus long que les frottements internes sont faibles. Pour qu'un son prenne naissance il faut le contact du milieu ambiant, généralement l'air. En présence d'air, le corps communique son état de vibration à la couche des molécules proches. Celles-ci entrent alors en collision avec les molécules de la couche suivante qui se mettent également à vibrer : ainsi de suite, une onde longitudinale de pression prend naissance, qui se déplace, dans toutes les directions, à la vitesse, c = 340 m/s. Cette mise en mouvement progressif réclame de l'énergie qui est fournie par le corps qui agit comme une source. Celle-ci s'épuise plus ou moins rapidement (exemple d'une corde qui serait pincée puis abandonnée à sa vibration) sauf si on l'entretient par un apport d'énergie (exemple d'une corde frottée en permanence avec un archet). Dans ce deuxième cas, la puissance de l'onde sonore en régime de croisière égale la puissance fournie par l'interprète.
Les molécules d'air atteintes par l'onde ne se déplacent pas globalement, elles ne font qu'osciller d'avant en arrière autour de leur position d'équilibre initial, communicant leur vibration aux molécules suivantes à la faveur des collisions multiples. Lorsque l'onde atteint les tympans d'un auditeur éventuel, ceux-ci se mettent également à vibrer, sollicitant le mécanisme physiologique de l'audition, pour autant que la fréquence soit audible c'est-à-dire comprise approximativement entre 16 Hz et 16000 Hz.
Ces généralités ne font aucune différence entre un son et un bruit. Les sons sont d'une façon ou d'une autre caractérisés par une fréquence fondamentale correspondant à une note identifiable par l'oreille. Ils constituent la matière première d'un langage musicalement exploitable. Des bruits bien choisis peuvent certes intervenir occasionnellement dans une partition mais ils doivent rester l'exception. Le point commun aux sons de toutes natures est de respecter le modèle harmonique où, par définition, les composantes sont sinusoïdales.
On lit parfois qu'un son doit être périodique et que c'est même ce qui le différencie d'un bruit mais c'est inexact, précisons. La plupart des instruments de musique n'émettent pas qu'un seul son sinusoïdal de fréquence, f1, mais, simultanément, une infinité de sons sinusoïdaux, dits partiels, de fréquences, fn (n = 1, 2, 3, ...). En toute généralité, ces fréquences se répartissent irrégulièrement, d'où le son résultant n'est pas périodique (Cas inharmonique), ce qui ne signifie nullement qu'il s'en trouve inexploitable, nous en verrons des exemples. Il est cependant vrai que les cas particuliers où les fréquences sont toutes multiples d'une fréquence fondamentale, fn = n f1, sont privilégiés, en musique, car l'onde sonore est alors rigoureusement périodique (Cas harmonique) et cela facilite le dialogue des instruments en prévenant certains battements parasites. Dans ces cas seulement, les sons partiels portent le nom de sons harmoniques.
Note à l'usage des (apprentis) physiciens ou musiciens. Le vocable "harmonique" peut être source de confusion, revêtant (au moins) deux significations qu'on ne lève à coup sûr qu'en distinguant leurs antonymes, "inharmonique" et "anharmonique". Les systèmes élastiques qui vibrent à faible amplitude (régime dit des petites oscillations) possèdent une propriété qui les rend particulièrement attrayants : leurs modes propres de vibrations sont sinusoïdaux, de fréquences, fn, et surtout ces fréquences sont indépendantes de l'amplitude de leur vibration. On les dit (in)harmoniques, une propriété qui est appréciée en musique car elle garantit que la hauteur du son émis ne dépend pas de l'intensité du geste de l'interprète, une stabilité bienvenue. Lorsque les modes de vibration respectent en outre la propriété, fn = n f1, ils sont dits harmoniques, c'est la situation idéale. Lorsque les mêmes systèmes sont sollicités trop intensément, les oscillations cessent d'être petites et ils perdent ces belles propriétés : ils deviennent anharmoniques (Cloches d'église, enclumes, etc). Dans ce qui suit, tous les systèmes étudiés sont au moins inharmoniques (glockenspiel, xylophone, marimba et même le piano dans ses registres exrêmes de cordes raides) sinon harmoniques (famile des cordes minces).
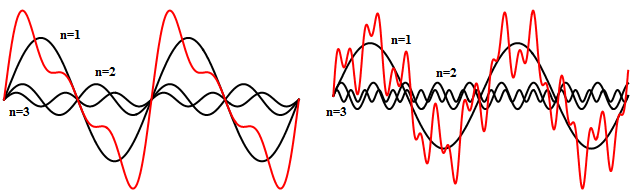
Les figures ci-dessous illustrent les cas harmoniques et inharmoniques. Elles représentent trois partiels sinusoïdaux ainsi que leur enveloppe résultante (en rouge) : à gauche, tout est simple, l'enveloppe du signal sonore est rigoureusement périodique et elle correspond à une note parfaitement définie. A droite (cas inharmonique), l'enveloppe cesse d'être périodique mais elle conserve une allure pseudopériodique à laquelle l'oreille se laisse prendre, lui associant une pseudo-fréquence correspondant à (une hauteur de) note subjective. Les sons pseudopériodiques doivent être traités avec prudence dans les cas fréquents où on les superpose car ils peuvent engendrer des battements indésirables (phénomène de dissonance).
Dans tous les cas, l'oreille reçoit un signal sonore caractérisé par une pression variant selon une loi du type :
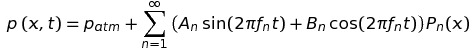
Dans cette formule, les coefficients An et Bn dépendent de l'instrument utilisé et de son mode d'emploi. Lorsque fn ≠ n f1 (cas inharmonique), ce développement en série infinie porte le nom des deux mathématiciens français qui ont contribué à son étude (vers 1836), à savoir Charles Sturm (1803-1855) et Joseph Liouville (1809-1882). Lorsque fn = n f1 (cas harmonique), il porte le nom de leur collègue Joseph Fourier (1768-1830), qui avait réglé ce cas particulier quelques années plus tôt.
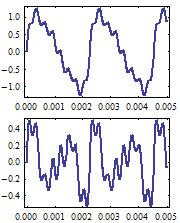
Le premier terme de la série infinie est généralement perçu par l'oreille comme dominant, d'où une fréquence attribuée au son valant, f1. Les autres fréquences, fn (n>1) correspondent à autant de sons partiels qui s'additionnent au fondamental, en enrichissant le timbre sans vraiment en modifier la fréquence perçue. Cependant, si l'on filtre un son du côté des basses fréquences de telle façon que la composante fondamentale, de fréquence, f1, soit absente, on observe, dans le cas harmonique, que cela ne modifie en rien la fréquence perçue qui demeure égale à f1, PGCD des fréquences restantes (f2, f3, f4, etc). Il n'y a rien de magique là-dessous comme le montre le graphe ci-contre, représentant une série de Fourier complète (en haut) ou amputée de sa composante fondamentale (en bas). Dans les deux cas, le signal apparaît périodique avec la même fréquence, f1. Par exemple, un grand piano de concert ne donne jamais à entendre pleinement la vibration à 27.5 Hz qu'implique sa note la plus grave (la0), sa table d'harmonie est bien trop petite pour résonner à une fréquence aussi basse (ce que confirmerait n'importe quel instrument de mesure). Pourtant si vous écoutez (de préférence en salle) le début de la Rhapsodie n°2, opus 79, de Brahms, vous entendez bien un son particulièrement grave que vous associez à cette note.
Classification des instruments de musique
La plupart des instruments de musique naissent de la rencontre d'un système oscillant et d'un système résonant. La classification raisonnée "Hornbostel-Sachs" (1914), qui ne se restreint pas aux instruments de l'orchestre symphonique, les range parmi cinq catégories, en fonction de la nature du support physique qui vibre. Ce peut être :
- Une plaque de métal (vibraphone, glockenspiel, etc) ou de bois (xylophone, marimba, etc) produisant un son défini, ou plus généralement n'importe quel objet massif (triangle, cymbale, etc) produisant un son indéfini (Famille des idiophones). Dans tous les cas, la vibration brute se transmet dans l'air ambiant sans nécessairement transiter par un espace résonant.
- Une membrane tendue, refermant éventuellement un espace résonant : tambour, timbales, etc (Famille des membranophones).
- Un ensemble de cordes tendues, le plus souvent par-dessus un chevalet s'appuyant sur une caisse de résonance : violon, piano, luth, clavecin, harpe, etc (Famille particulièrement nombreuse des cordophones).
- Une colonne d'air dans un conduit : orgue, flûte, clarinette, trompette, etc (Famille des aérophones).
- Un circuit électrique oscillant alimentant des haut-parleurs : synthétiseur, guitare électrique, thérémine, ondes Martenot, etc (Famille des électrophones).
Il ne suffit pas qu'une partie de l'instrument vibre, il faut encore que cette vibration gagne l'air ambiant sous la forme d'une onde sonore progressive. On peut décomposer le processus en trois temps :
- Le geste initial appartient à l'interprète qui excite l'oscillateur de façon appropriée (En insufflant de l'air, en frappant une corde, en la pinçant ou encore en exerçant une friction sur elle, etc). Si cet oscillateur était affranchi de tout frottement, il continuerait de vibrer sans amortissement jusqu'à la fin des temps et on n'entendrait aucun son puisque l'énergie mise en jeu resterait prisonnière de l'oscillateur. Ce n'est (heureusement !) pas réaliste car les frottements sont toujours présents, en particulier au contact de l'air, et cela nous arrange puisque ce que l'on veut, c'est entendre un son.
- On rend l'instrument effectif en précipitant l'amortissement de la vibration initiale : un dispositif mécanique intervient généralement, à ce stade, qui communique la vibration primitive à un volume d'air emprisonné dans un espace clos, dit de résonance (caisse, tuyau, etc). La fonction de cet espace résonant est d'accélérer le transfert d'énergie de l'oscillateur (qui s'amortit) vers l'air prisonnier (qui entre en vibration).
- L'air confiné transmet la vibration acquise à l'air extérieur avec lequel il communique par un système d'ouvertures (les ouïes). L'air étant de nature élastique, la vibration des couches directement en contact avec les ouïes se transmet de proche en proche aux couches successives : une onde sonore prend naissance qui rayonne dans toutes les directions de l'espace environnant, jusqu'à atteindre un auditeur éventuel. On comprend que l'intensité de l'onde sonore dépende de l'efficacité avec laquelle l'énergie de l'oscillateur est cédée à l'espace résonant puis communiquée aux premières couches d'air ambiant. L'amplification du son dû à l'espace résonant dépend donc de l'optimisation de cette transduction mécano-acoustique. Ce que le son gagne en intensité, par ce procédé, il le perd en durée. Lorsque l'oscillateur a réintégré son état de repos initial, il est prêt pour une nouvelle excitation donc une nouvelle note sans qu'il y ait chevauchement parasite.
On illustre ce qui vient d'être dit en considérant l'instrument le plus simple qui soit, le diapason.
Le cas d'école du diapason

Le diapason n'est pas un instrument de musique à proprement parler car le son qu'il émet est bien trop pauvre en partiels pour être exploitable mais la simplicité de son fonctionnement permet de fixer les idées de base. Cet instrument, qui serait à ranger dans la famille des idiophones, est constitué de deux branches métalliques parallèles dessinant un U étroit et allongé et dont la base est prolongée par une mince tige pouvant s'enficher, si on le souhaite, dans l'orifice d'une caisse de résonance de bonne longueur (Cf infra). Celle-ci est en forme de parallélépipède rectangle, ouvert sur une face latérale. Avant de poursuivre, vous pouvez visionner cette vidéo décrivant l'expérience du diapason (Référence : Physique à main levée, Université de Lille).
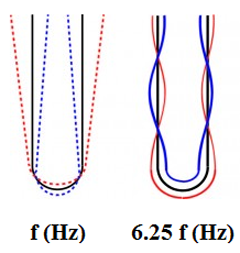
L'étude de cette double tige est un sujet d'étude classique, en acoustique physique. On y prédit que si l'on percute l'instrument avec un marteau en caoutchouc, on fait essentiellement vibrer les deux branches : 1) latéralement (= transversalement), 2) sinusoïdalement à une fréquence, f, dont la valeur dépend des caractéristiques physiques du diapason (masse volumique, longueur, etc) et 3) symétriquement (en opposition de phase), ce qui garantit l'immobilité du centre d'inertie.
D'autres modes symétriques existent simultanément dont le premier vibre à une fréquence nettement plus élevée, 6.25 f, soit deux octaves et demie plus haut. Si vous suivez, vous avez noté que 6.25 n'est pas un entier, ce qui prouve l'inharmonicité du diapason. C'est une caractéristique assez générale des idiophones qui limite leur intégration à l'orchestre symphonique.
La théorie prédit encore l'existence de modes asymétriques de vibration (en phase) dont vous trouverez la description ici. Les modes secondaires sont peu intenses et éphémères d'où ils influencent peu le timbre perçu. En résumé, dans le cas du diapason, le mode fondamental sinusoïdal est largement dominant produisant un son pur mais tellement détimbré qu'il est musicalement inutilisable.
Suspendu à un fil, dans une cloche vidée de son air, un diapason percuté peut vibrer très longtemps car il n'est sujet à aucun amortissement notable. Si l'on rétablit l'air dans la cloche, un son prend naissance mais il est peu intense car l'amortissement au seul contact de l'air demeure lent, alimentant fort peu l'onde sonore en énergie.
En mode symétrique dominant, la tige située à la base du U ne vibre pas latéralement. Par contre, rien ne s'oppose à ce qu'elle vibre verticalement (longitudinalement), comme suggéré sur la figure précédente, c'est même requis par l'immobilité du centre d'inertie. En conséquence, on peut saisir la tige entre les doigts sans amortir la vibration principale du diapason et l'introduire dans l'ouverture de la caisse de résonance : son oscillation longitudinale, bien que faible, suffit pour exciter, à la même fréquence, la vibration de la caisse toute entière, air compris. On entend que le son gagne en intensité et perd en durée.
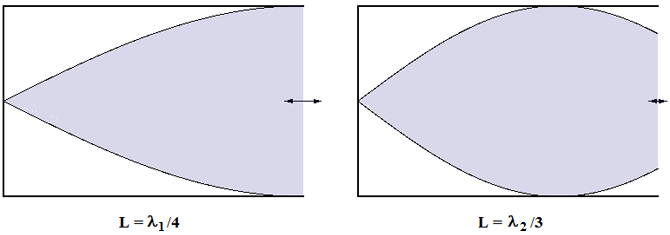
La dimension de la caisse doit être ajustée pour permettre un rayonnement maximum. Les figures ci-dessus illustrent les cas où l'on utiliserait une même caisse pour deux diapasons émettant des fréquences différentes, f1 = c/(4 L) et f2 = c/(3 L). La figure située à gauche illustre le cas idéal d'une longueur de caisse, L, valant le quart de la longueur d'onde émise, L = c/(4f) = 85/f, soit L = 193 mm, pour un la situé à 440 Hz. Dans ce cas, l'air vibre (longitudinalement) avec l'amplitude maximum au niveau de l'ouïe. La figure de droite représente la même caisse recevant un diapason de fréquence plus grande (f2 = 4f1/3) : elle cesse d'être idéale car elle est trop longue du facteur 4/3. Ce qu'il faut en tous cas retenir, c'est qu'une caisse de résonance donnée n'est idéale que pour une seule fréquence de diapason ou, si l'on préfère, qu'il faut idéalement autant de (longueur de) caisses de résonance qu'on possède de diapasons de fréquences distinctes.
Un grand nombre d'instruments de musique fonctionnent sur le principe d'un résonateur qui précipite le transfert d'énergie de l'oscillateur vers l'onde sonore. Plus il le fait rapidement plus la note émise gagne en intensité et s'écourte au profit de la note suivante, c'est double bénéfice. Les instruments (plus) intéressants (que le diapason) possèdent plusieurs oscillateurs couplés à un nombre variable de résonateurs éventuellement un seul. On distingue :

- Les instruments à sons fixes (piano, clavecin, marimba, etc) qui possèdent autant d'oscillateurs individuels qu'il y a de notes à produire. Le système résonant peut consister en un résonateur unique (caisse de résonance, table d'harmonie, ...), c'est le cas du piano, ou en autant de résonateurs calibrés et couplés individuellement aux oscillateurs, c'est le cas du marimba. Dans cette éventualité, chaque résonateur est d'autant plus grand que la note à accorder est grave (donc que sa fréquence est basse).

- Les instruments à sons variables (violon, trombone à coulisse, thérémine, etc) où le nombre des oscillateurs est bien moindre que celui des notes à produire. C'est alors la technique de l'instrumentiste qui compense ce manque en diversifiant la position des doigts sur les cordes, l'allongement de la coulisse, etc. Dans ce cas, un résonateur unique devrait idéalement convenir à toutes les notes, chose que nous savons impossible. Ceci pose des problèmes techniques difficiles aux facteurs dans la recherche du meilleur compromis qui ne sacrifie aucune note, des plus graves aux plus aiguës. Dans le cas du violon, ce problème a occupé plusieurs générations de luthiers célèbres.
Le diapason n'est d'aucune utilité dans la pratique musicale sauf peut-être pour les chanteurs qui veulent repositionner leur voix. Il aide cependant à comprendre les principes physiques qui président à la génération de l'onde sonore. Pour aller plus loin, il est nécessaire de détailler les modes de vibration des systèmes usuels utilisés en organologie. Nous nous limiterons 1) à la corde élastique idéale, au comportement harmonique fort (violon), 2) à la lame épaisse, au comportement inharmonique (marimba) et 3) au cas intermédiaire (piano). Nous n'étudierons pas, dans les détails, les vibrations des membranes bidimensionnelles et pas du tout celles, compliquées, des tuyaux sonores (qui cumulent l'étude des vibrations d'une colonne d'air, la présence éventuelle d'une anche et la nécessité d'un pavillon au profil caractéristique destiné à resserrer des partiels trop espacés). Le lecteur qui souhaiterait approfondir ces cas plus difficiles peut consulter, en ligne, l'ouvrage encyclopédique, The Physics of musical Instruments, de N. H. Fletcher & T. D. Rossing (Springer).
Vibrations de la corde idéale
Une corde idéale est, par définition, dépourvue de raideur. On peut la déformer sans effort et la déposer sur une table : elle y demeure sans réaction. Elle est entièrement caractérisée par un ensemble de paramètres physiques que l'on note comme suit, une fois pour toutes : masse volumique (ρ), longueur (L), section (S), masse par unité de longueur (μ = ρ S) et tension interne (T).
Si l'on perturbe l'état d'une corde idéale tendue entre ses extrémités fixes, par exemple en la pinçant, elle se déforme. Une fois relâchée, elle tente de revenir à sa position initiale mais elle n'y parvient pas immédiatement. Au contraire, elle se met à osciller de part et d'autre de cette position de repos avec une fréquence, f1, qui dépend des valeurs de ses paramètres physiques. Elle vaut :
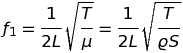
En l'absence de frottement, cette corde oscillerait éternellement. L'étude mathématique de ce cas idéal est classique : elle repose sur la résolution de l'équation de propagation des ondes, ∂ttu(x,t) = c2 ∂xxu(x,t), où u(x,t) représente l'ordonnée des points de la corde à tout instant (on a posé, pour abréger : c2 = T/μ). La solution est connue depuis les travaux de Daniel Bernoulli (1700-1782) et Jean le Rond d'Alembert (1717-1783) et, en notations modernes, on l'exprime sous la forme d'un développement en série de Sturm-Liouville :
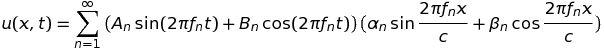
Dans cette série, les coefficients αn et βn se déduisent des conditions aux limites imposées à la corde. Celle-ci étant fixée à ses extrémités, on doit avoir u(0,t) = u(L,t) = 0, pour tout t, ce qui annule les coefficients βn et impose fn = n f1 = n (c/2L). Après simplifications, la série se réduit à la forme de Fourier, caractéristique du cas harmonique fort (Cf supra) :
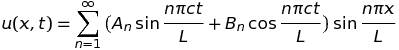
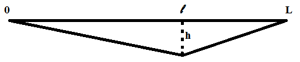
Les coefficients, An et Bn, se calculent ensuite en fonction de la déformation initiale imposée à la corde. Dans le cas particulier où la corde est pincée "en dent de scie" à une distance, ℓ, de son extrémité (imposant un déplacement, u(ℓ, 0) = h, et une vitesse nulle, ∂tu(x,t)|t=0 = 0), cette solution s'écrit simplement :
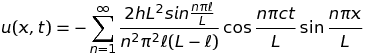
Si vous êtes allergique à toute forme de calcul, vous pouvez sauter ce paragraphe sans dommage pour la compréhension ultérieure; sinon vous pouvez à tout le moins vérifier que cette solution répond à la question posée :
- L'équation des ondes est vérifiée à la condition que la vitesse, c, de propagation de l'onde le long de la corde vérifie la relation, c2 = T/μ, quelle que soit la fréquence (aucune dispersion).
- Les conditions initiales sont respectées : à l'instant t=0, la corde est bien déformée en dent de scie, u(x,0)=-hx/ℓ si 0≤x≤ℓ et u(x,0)=-h(L-x)/(L-ℓ) si ℓ≤x≤L, et elle est immobile, ∂tu(x,t)|t=0 = 0.
- Les conditions aux limites sont également respectées : la corde est fixe aux extrémités puisque u(0,t) = u(L,t) = 0.
Le point important est que les fréquences des sons partiels sont toutes multiples de la fréquence fondamentale (cas harmonique), on a en effet : fn = n f1 = n c/(2L). Le premier terme du développement de Fourier de la solution, u(x,t), est en principe dit fondamental et les suivants sont dits harmoniques mais, en pratique, l'usage autorise de parler d'harmonique de rang n, y compris pour le fondamental qui occupe alors le rang 1.
Les 21 figurines suivantes représentent l'évolution du profil de cette corde idéale, pincée initialement aux deux tiers de sa longueur (On a exagéré fortement la hauteur de la dent de scie pour plus de lisibilité). Elles se lisent dans l'ordre normal, de gauche à droite sur chaque ligne, et elles représentent l'état de la corde tous les vingtièmes de période. Au terme d'un cycle complet (21ème figurine), la corde reprend sa position de départ et l'oscillation recommence à l'identique.

Cette analyse de Fourier appelle les remarques suivantes :
- Même si vous avez ignoré les calculs, vous devez retenir que la déformation initiale imposée à la corde a déterminé les valeurs numériques des coefficients de la solution de Fourier donc l'amplitude des sons harmoniques donc le timbre perçu. C'est parce que la déformation initiale (en dent de scie) est non sinusoïdale que les harmoniques sont présents.
-
A contrario, si la corde avait été perturbée initialement en dessinant une arche complète de sinusoïde reliant ses extrémités fixes, elle aurait conservé éternellement cette allure sans faire apparaître le moindre son harmonique car cette sinusoïde aurait précisément coïncidé avec le son fondamental (Le même raisonnement vaudrait pour n'importe quel harmonique). En clair, la corde aurait oscillé de façon stationnaire, comme indiqué sur la figure ci-contre, ne pouvant engendrer qu'un son complètement détimbré. Ce cas de figure ne se produit (heureusement) jamais, en pratique, puisqu'il n'est pas envisageable de déformer la corde de cette façon rien qu'avec les doigts.
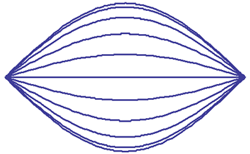
Vibration stationnaire - Revenant au cas plus réaliste de la déformation en dent de scie, on constate que la position de cette dent (la valeur de ℓ) influe sur le spectre des harmoniques à cause du facteur, sin(nπℓ/L). En particulier, ce ne serait pas une bonne idée d'exciter la corde en son milieu, ℓ=L/2, car cela aurait pour conséquence d'éteindre les harmoniques de rangs pairs d'où un appauvrissement du timbre. En fait, l'exciter au tiers de sa longueur ne serait guère mieux puisque, cette fois, ce seraient les harmoniques de rangs multiples de 3 qui seraient éteints. L'idéal est donc d'éviter de solliciter la corde en des points tels que le rapport, ℓ/L, soit une fraction simple. Bien sûr aucun violoniste ne se préoccupe de calculs aussi savants, il sait par expérience où la corde doit être attaquée pour que l'instrument sonne bien.
- Le développement de Fourier trouvé décrit le mouvement périodique de la corde mais pas du tout l'allure de l'onde sonore parvenant à l'auditeur. La raison essentielle est que la caisse de résonance de l'instrument modifie inexorablement le spectre des harmoniques donc le timbre de l'instrument tel qu'il sera perçu et analysé par l'oreille. La caisse de résonance, disons d'un violon, ne peut convenir idéalement à toutes les fréquences générées par les cordes. La conséquence inévitable est qu'elle altère l'intensité des harmoniques de façon variable et d'ailleurs largement imprédictible. Il faut s'en faire une raison, il n'est pas possible de tirer parti des lois de l'acoustique physique pour prédire le comportement d'une caisse donnée donc de calculer a priori le profil d'une caisse qui serait meilleure que les autres. Cela a été tenté maintes fois mais n'a jamais réussi. Certes, on a construit maints violons acceptables en tentant de tels calculs mais le résultat n'a jamais égalé le produit fini, fruit de l'intuition crémonaise. Dépités par les limites de leur science, les savants de toutes les époques ont invoqué le rôle présumé important de contingences peu formalisables, telle la qualité du bois utilisé, en particulier ses conditions de séchage et de vieillissement, ou la nature jamais vraiment élucidée du vernis utilisé. Personne à ce jour n'a jamais été en mesure de confirmer ou d'invalider ces supputations invérifiables, d'où le mystère entourant les meilleurs instruments baroques demeure largement entier.
- L'intensité du son émis par la corde vibrante est évidemment liée à l'énergie dépensée lors de sa mise en mouvement. Contentons-nous d'envisager le cas simple d'une corde pincée initialement puis abandonnée à elle-même. A l'instant initial, la corde déformée n'est porteuse que d'une énergie potentielle, U0, car étant immobile à cet instant, elle ne possède aucune énergie cinétique (K0=0). Lorsque la corde entre en oscillation, elle se détend, convertissant progressivement son énergie potentielle, U, en énergie cinétique, K, et inversement un quart de période plus tard. L'essentiel est de comprendre qu'en l'absence momentanée de frottement, l'énergie totale se conserve, à tout instant sous la forme :
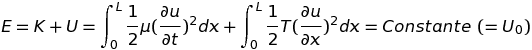 On peut préciser les valeurs de chaque terme dans le cas particulier de la corde pincée en dent de scie, il suffit d'utiliser la formule trouvée pour u(x,t) dans ce cas. La figure ci-contre montre que pour un écartement donné c'est en pinçant la corde en son milieu que l'on dépense et donc qu'on y stocke l'énergie minimum. Cette position requiert sans doute un effort minimum de l'interprète mais nous verrons qu'elle ne convient pas si l'on recherche un son brillant et puissant.
On peut préciser les valeurs de chaque terme dans le cas particulier de la corde pincée en dent de scie, il suffit d'utiliser la formule trouvée pour u(x,t) dans ce cas. La figure ci-contre montre que pour un écartement donné c'est en pinçant la corde en son milieu que l'on dépense et donc qu'on y stocke l'énergie minimum. Cette position requiert sans doute un effort minimum de l'interprète mais nous verrons qu'elle ne convient pas si l'on recherche un son brillant et puissant.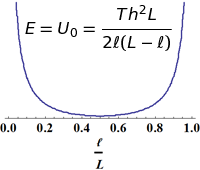
Energie dépensée en fonction du point d'attaque
Les considérations qui précèdent ne concernent que le mode principal de vibration des cordes, dit transversal. Une théorie complète doit également prendre en compte qu'une corde vibre aussi longitudinalement à cause de son allongement initial. De même, la friction de l'archet provoque un enroulement local de la corde donc une vibration torsionnelle. Bien que ces modes soient accessoires, du fait de leur intensité relativement faible, ils participent au timbre de l'instrument. Cela saute particulièrement aux oreilles aguerries lorsqu'on compare un violon moderne à un violon ancien dont les cordes sont en boyau.
Le violon et la corde idéale
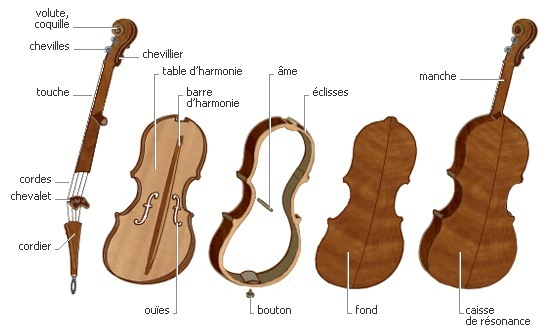
Tout violon résulte de l'assemblage par emboîtement et collage d'environ 80 pièces en bois (semi-)nobles (érable, épicéa et exotiques, ébène et palissandre). Il doit être capable de résister à la tension de quatre cordes idéales destinées (le plus souvent) à être frottées avec un archet. La figure ci-dessus représente cet instrument en vue éclatée afin de préciser l'essentiel du jargon utilisé.
- Les cordes sont tendues, par-dessus un chevalet, entre deux extrémités situées de part et d'autre de l'instrument; l'une est inerte, c'est le bouton de fixation, et l'autre est active au niveau des chevilles qui, en tournant, permettent de régler les tensions (Un réglage fin supplémentaire existe éventuellement sous la forme d'un tendeur situé au-delà du chevalet, au niveau du cordier, mais il n'est pas absolument indispensable. Un calcul simple montre en effet qu'une erreur relative sur la tension, ΔT/T, produit un déplacement d'intervalle de l'ordre de ΔI ≈ 260 ΔT/T, soit 7.8 cents (un tiers de comma) en cas d'erreur sur T de l'ordre de 3 %). Les tensions régnant au sein de chaque corde varient d'une facture à l'autre et il n'y a pas d'autres références possibles que commerciales (Valeurs moyennes : sol3 (45N), ré4 (49N), la4 (54N), mi5 (78N)). Ensemble, les 4 cordes à vide sont responsables d'une tension longitudinale avoisinant les 220 Newtons, l'équivalent d'un poids de 22 kg. Quand on sait que, tout compris, un Stradivarius ne pèse pas plus que 0.360 kg, on mesure la performance que représente sa simple résistance mécanique.
- Le chevalet est l'organe essentiel qui assure la transmission de la (composante verticale de la) tension des cordes vers la table d'harmonie. L'effort exercé sur la table d'harmonie est loin d'être négligeable. Les cordes faisant un angle de l'ordre de 81.4° avec le chevalet surélevé à cet effet, le cosinus de cet angle impose que 15% de l'effort total soient transmis perpendiculairement à la table d'harmonie via le chevalet, soit environ 33 N (3.3 kg). Cet effort menaçant la caisse d'implosion, une âme en bois, en forme de cylindre, relie la table d'harmonie au fond de la caisse. Elle part du pied du chevalet situé à l'aplomb de la corde la plus aiguë (mi5) car c'est celle qui supporte la tension maximum. L'âme n'a pas pour seule vocation de renforcer la caisse, elle assure également une meilleure transmission de la vibration des cordes vers le fond de la caisse donc finalement vers l'air emprisonné dans l'espace résonant.
- La barre d'harmonie est une longue tige en bois collée sur la face intérieure de la table d'harmonie, dans le sens longitudinal et à l'aplomb de la corde la plus grave (sol3); fonctionnant comme une antenne, elle favorise également la transmission de la vibration des cordes vers l'air prisonnier de la caisse.
Deux questions intriguent éventuellement l'amateur curieux : pourquoi, depuis l'époque de Stradivarius, le violon (et les instruments apparentés) épouse-t-il cette forme étrange "en huit", et pourquoi les ouïes dessinent-elles ce "f" allongé caractéristique ? La réponse à la première question est facile : l'ancêtre médiéval du violon, la vielle (vièle, vedel, vihuela, fiddle, ...), a présenté très tôt l'ébauche d'une échancrure au niveau du chevalet. Celui-ci était moins haut, à l'époque, et il était rectangulaire. En le chevauchant, les cordes étaient inévitablement situées dans un même plan, ce qui avait pour conséquence qu'on ne pouvait jouer une corde intermédiaire sans les jouer toutes. Seules les cordes extrêmes pouvaient être jouées individuellement, encore fallait-il pouvoir incliner l'archet. C'est pour ménager le passage de l'archet que l'échancrure s'est développée et absolument pas pour améliorer les performances acoustiques de la caisse de résonance. La deuxième question est plus difficile et elle a trouvé récemment une réponse surprenante. Les ouïes n'ont pas toujours présenté la forme en "f" que nous leur connaissons aujourd'hui : partant, vers 1000-1100, d'une forme circulaire quasiment complète, elles ont évolué vers une demi-lune avant de se restreindre à un "C" majuscule qui s'est finalement allongé et déformé jusqu'à atteindre le profil actuel. Une équipe du MIT, dirigée par Nicholas Makris, a tenté d'expliquer cette évolution en examinant plusieurs générations d'instruments, rangés dans l'ordre chronologique. Leur étude (Proc. R. Soc.A 471:20140905) repose sur une mesure minutieuse des altérations successives subies par les ouïes. Ils ont trouvé qu'elles ont suivi un processus d'essais et d'erreurs. En tentant de recopier le plus fidèlement possible les instruments en leur possession, chaque génération de luthiers a buté sur le problème de la taille fidèle des ouïes à même le bois : l'équipe de Makris a pu établir qu'un dérapage de l'ordre de 2 % n'était pas rare. En postulant que les artisans ont chaque fois retenu la variante offrant le meilleur son, ils sont parvenus à cette conclusion que les ouïes en forme de f ont été l'aboutissement d'une évolution de type darwinienne, nullement d'une intuition aussi géniale que subite et encore moins d'un calcul prémédité. A l'appui de cette thèse, il y a lieu de noter que les modèles ultérieurs, calculés et assemblés par Félix Savart (1791-1841) (Violon trapézoïdal avec ouïes rectangulaires) et par Francis Chanot (1788-1828) (Violon guitare avec ouïes en formes de virgules), n'ont rien apporté leur permettant de rivaliser avec les modèles anciens.
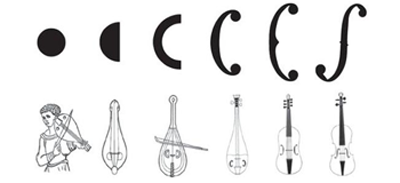
En fonction du diapason souhaité (la4 normalement situé à 440 Hz mais éventuellement ramené à 415 Hz en musique ancienne, soit un demi ton tempéré d'écart), les cordes à vide sont réglées en atelier selon une progression par quintes tempérées, sol3 (196 Hz), ré4 (293.7 Hz), la4 (440 Hz) et mi5 (659.3 Hz). Les autres notes s'obtiennent par le jeu de l'interprète qui raccourcit la corde jouée en la pressant d'un doigt contre la touche. L'instrument peut ainsi couvrir 4 octaves, de sol3 (196 Hz) à sol7 (3136 Hz). D'instinct, un violoniste préfère les quintes pythagoriciennes aux quintes tempérées (Rappel de théorie ici), d'où il a tendance à altérer légèrement les intervalles afin de les ajuster. Le problème est qu'il joue rarement seul mais souvent avec un pianiste qui lui dicte le tempérament égal. Dans ce cas, les bons compromis font les bons duos, tel le couple légendaire à la scène qu'ont formé Clara Haskil et Arthur Grumiaux (Intégrale inégalée des Sonates de Beethoven).
C'est une des tâches du luthier d'ajuster les paramètres physiques des cordes à la formule connue, f1 = (1/2L)✓(T/ρS), ce qu'il peut faire d'une infinité de manières puisque 4 paramètres sont disponibles. Trois seulement sont effectifs cependant car la norme veut que toutes les cordes soient de même longueur utile, L = 0.328 m. A l'époque (pré)classique, Leopold Mozart recommandait, en outre, que les tensions des cordes soient égales afin d'éviter tout couple de forces susceptible de contraindre le chevalet (Note : il est peu probable que Mozart père désignait la valeur physique de cette tension, telle qu'on la mesure aujourd'hui, en Newtons. Il désignait plus probablement la tension ressentie par l'instrumentiste, une valeur nettement plus subjective). Aujourd'hui, avec des chevalets renforcés, cette recommandation n'est plus de mise ni rigoureusement respectée. Au cours des décennies, un grand nombre de combinaisons ont été essayées concernant les paramètres, T, ρ et S (= πD2/4, où D est le diamètre de la corde) : elles ont abouti aux choix actuels où subsistent cependant de nombreuses variantes. Les données numériques qui suivent ne sont donc données qu'à titre indicatif puisqu'elles changent d'une facture à l'autre.
| sol3 (196 Hz) | ré4 (293.7 Hz) | la4 (440 Hz) | mi5 (659.3 Hz) | |
|---|---|---|---|---|
| Tensions | 45 N | 49 N | 54 N | 78 N |
| Diamètres | 1.55 mm | 1.08 mm | 0.76 mm | 0.58 mm |
| Masses volumiques | 1578 kg/m3 | 1440 kg/m3 | 1440 kg/m3 | 1440 kg/m3 |
A l'époque baroque, toutes les cordes étaient en boyau (de mouton, pas de chat !), à raison de 5 cordes finement tressées par mouton. La corde de sol était filée à l'aide d'un fin fil d'argent ou de cuivre, soigneusement enroulé afin de ne pas nuire à l'élasticité. Ces cordes de faible raideur délivrent un son chaleureux mais elles coûtent cher et elles tiennent difficilement la tension qu'on leur impose, nécessitant un réaccordage fréquent. Cependant elles demeurent un "must" en musique ancienne. Au 20ème siècle, on est progressivement passé aux cordes en acier (moins chères, plus stables, plus sonores mais hélas plus raides - Eacier≈ 3Esynth≈ 7Eboyau - et plus froides) puis aux cordes synthétiques (du type nylon), éventuellement filées d'aluminium traité, au bilan un bon compromis (sauf en musique ancienne). Hors filage métallique, les matières constitutives des cordes sont de masses volumiques très différentes, par exemple : Boyau (1276 kg/m3), Acier (7800 kg/m3) et Nylon (1000 kg/m3).
Le violoniste dispose d'un grand nombre de techniques pour varier le son. En pratique, la distance, ℓ, de l'archet par rapport au chevalet et la vitesse de l'archet sont déterminantes sur la puissance rayonnée, selon une loi du type v/ℓ2. C'est le jeu près du chevalet qui est le plus utile à la puissance du son, ce qui est logique puisque c'est en ce voisinage que s'opère la meilleure transduction vers la table d'harmonie. L'archet doit être actionné perpendiculairement aux cordes afin d'atténuer les modes de vibrations longitudinales de la corde, sources de battements parasites. La finesse des cordes prémunit contre les vibrations torsionnelles et l'inharmonicité (Cf infra) qui causeraient les mêmes effets indésirables.
Le violon moderne n'a guère évolué depuis les travaux de l'école de Crémone (Stradivarius, Guarnerius, Amati, ... et n'oubliez pas de très beaux instruments réalisés en Allemagne et en Bohême). Les modifications principales, effectuées au 19ème siècle, ont essentiellement eu pour but de renforcer l'intensité du son (Remplacement des cordes en boyau par des cordes métalliques, allongement du manche, renforcement de la barre d'harmonie). L'école de Mirecourt, en France, a prouvé qu'il était parfaitement possible de concevoir des violons en tous points remarquables et à toutes les époques. J'ai entendu récemment l'excellente violoniste, Tatiana Samouil, jouant un superbe instrument conçu par Sébastien Auguste Bernardel (1802-1870) !
La théorie du jeu de violon n'est simple que si l'on pince les cordes en pizzicato. Dans ce cas, les cordes répondent en vibrant comme il a été décrit. Le jeu habituel, impliquant le frottement de l'archet, est nettement moins simple à formaliser du fait qu'il implique une succession d'accrochages-décrochages où la corde commence par suivre l'archet (sans vibrer) tant que la force de frottement (statique) surpasse la force de rappel de la corde puis se libère lorsque l'inverse se produit. Le rôle de la colophane dont on enduit l'archet est essentiel si l'on veut maîtriser cette source de discontinuité mais ces subtilités ne rentrent pas dans un exposé élémentaire. Tout virtuose sait qu'un archet doit être digne du violon sur lequel il joue et que l'acquisition d'un "François Xavier Tourte (1748-1835)" se négocie vers les 100000 euros.
Quelques grandes formations symphoniques européennes (Vienne, Berlin) se distinguent par l'excellence de leur section des cordes. Dans son enregistrement daté de 1976, Herbert von Karajan a obtenu des cordes de "sa" Philharmonie de Berlin un son "filé" jamais égalé dans le premier mouvement de la Symphonie n°4 de Jean Sibelius (Ecoutez à partir de 6:00). Il ne reste malheureusement plus que des enregistrements de studio pour vous en convaincre.
Vibrations de la lame épaisse
A l'opposé de la corde idéale, unidimensionnelle et filiforme, on trouve la lame (ou la tige) rigide, de section, S, et de longueur, L. Qu'elle soit en bois dur ou en métal, de forme parallélépipédique aplatie (lame) ou cylindrique (tige), la théorie qui décrit sa vibration repose sur une équation de propagation des ondes plus compliquée, où interviennent le module d'Young, E, la (surface de) section, S, la masse volumique, ρ, la masse linéique, μ = ρS, et un facteur de forme, g, valant e/✓12 dans le cas d'une lame d'épaisseur, e, et r/2 dans la cas d'une tige cylindrique de rayon, r. L'équation se note : ∂ttu(x,t) + c2g2 ∂xxxxu(x,t) = 0, où l'on a posé c2 = ES/μ pour abréger. On voit qu'elle demeure du deuxième ordre selon le temps mais qu'elle passe à l'ordre 4 pour ce qui concerne la dimension spatiale, x. On peut montrer que la solution de cette équation est du type Sturm-Liouville :
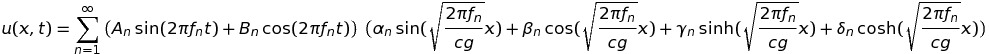
Dans cette série, les coefficients αn, βn, γn et δn se déduisent des conditions aux limites imposées à la lame, qui s'expriment différemment selon ses modes de fixation :
- A une extrémité libre, on doit avoir, ∂xxu(x,t) = 0 (courbure nulle) et ∂xxxu(x,t) = 0 (torsion nulle).
- A une extrémité encastrée, on doit avoir, u(x,t) = 0 (déplacement nul) et ∂xu(x,t) = 0 (pente nulle).
- A une extrémité simplement posée sur un support, on doit avoir, u(x,t) = 0 (déplacement nul) et ∂xxu(x,t) = 0 (courbure nulle).
Les figures ci-dessous, empruntées à l'ouvrage déjà cité de Fletcher & Rossing mais annotées différemment, présentent les quatre premiers partiels dans trois cas remarquables :
- (a) la lame est suspendue (par exemple à un fil) et ses extrémités sont libres de vibrer (carillon, xylophone, ...), u''(0,t) = u'''(0,t) = u''(L,t) = u'''(L,t) = 0, ce qui donne tous calculs faits : fn = (zn/π)2 (π c g/2L2) avec zn racines de -1 + cos(z)ch(z) = 0.
- (b) la lame est encastrée à une extrémité et libre à l'autre extrémité (guimbarde, sanza africain, ...) , u(0,t) = u'(0,t) = u''(L,t) = u'''(L,t) = 0, ce qui donne tous calculs faits : fn= (zn/π)2 (π c g/2L2) avec zn racines de 1 + cos(z)ch(z) = 0.
- (c) la lame est posée, à ses extrémités, sur deux supports, u(0,t) = u''(0,t) = u(L,t) = u''(L,t) = 0, ce qui donne tous calculs faits : fn = (zn/π)2 (π c g/2L2) avec zn (= n π) racines de sin(z) = 0 donc après simplifications, fn= n2 (π c g/2L2).
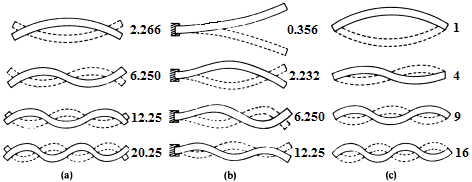
Les nombres qui figurent en regard de chaque mode donnent la fréquence d'oscillation dans l'unité, (π c g/2L2). Si l'on compare les modes fondamentaux dans les trois cas, on constate que, tous paramètres physiques égaux, c'est la lame encastrée qui sonne le plus grave et la lame libre qui sonne le plus aigu. Par ailleurs, seule la lame posée aux deux extrémités respecte un schéma harmonique fort où manquent cependant les harmoniques qui ne sont pas carrés parfaits (n = 2, 3, 5, ...). La lame suspendue respecte un schéma inharmonique tel que les fréquences des partiels successifs sont proportionnelles à ¼{3.01062, 52, 72, 92, etc}.
Les instruments tubulaires (carillon, etc) ou lamellaires (glockenspiel, xylophone, marimba, etc) reposent sur le modèle de la lame à extrémités libres (de vibrer, cf (a) sur la figure précédente). Soit les tubes sont suspendus à des fils non contraignants soit les lames sont posées et discrètement nouées par des fils sur deux supports situés à un noeud de vibration principale (bien visible sur la figure (a)). Le modèle (b) intervient chez les instruments à vents munis d'une anche (non étudiés ici) et le modèle (c) n'est pas vraiment utilisé en musique.
On excite les plaques en les frappant à l'aide d'un ou plusieurs maillets simultanément. L'endroit où l'on frappe influe sur les partiels que l'on veut mettre en évidence : par exemple, il ne servirait à rien de frapper une lame à l'emplacement d'un noeud de vibration, celle-ci ne répondrait pas.
Si l'on s'en tient à des lames parallélépipédiques, de dimensions, L×ℓ×e, les modes transversaux de la lame libre sont donnés par la formule (zn = {4.73, 7.85, 11., 14.14, ...}) :
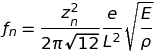
Pour un bois de rose du Brésil, ρ vaut de l'ordre de 740 kg/m3 et E vaut entre 2.8 109 et 1.6 1010 selon le mode de taille du bois par rapport à la fibre (resp. ⊥ et ∥). Il ne subsiste que deux paramètres pour influer sur la fréquence : la longueur et l'épaisseur de la lame, et ils agissent en sens inverse. On voit que la largeur, ℓ, n'intervient pas à ce stade et cela pourrait surprendre ceux qui savent que les lames d'un clavier de marimba ont tendance à être plus larges dans le grave (clavier progressif). L'explication est fournie dans une note ci-après.
Une complication déjà mentionnée à propos des cordophones se retrouve aggravée chez les lamellophones : une lame peut vibrer de plusieurs autres façons, en particulier en mode torsionnel. Cela peut entraîner un léger abaissement des fréquences calculées par la formule précédente.
Quelques lamellophones (glockenspiel, xylophone ou marimba)
Ces instruments plus ou moins sophistiqués utilisent le principe de la lame vibrante. Pour rappel, les lames sont nouées sur un support en position nodale afin que le contact n'empêche pas la lame de vibrer librement (Cas (a) évoqué en théorie).

A première vue, les claviers du glockenspiel, du xylophone et du marimba se ressemblent : tous disposent leurs lames en suivant la progression des touches blanches et noires d'un clavier chromatique de piano. Cependant, si l'on jette un coup d'oeil sur la face cachée des lames, on observe des différences qui expliquent les particularités du timbre de chacun. Des trois instruments, c'est incontestablement le marimba qui résonne avec le plus grand raffinement. Voici quelques éléments de théorie qui éclairent ces différences.
- Les lames du glockenspiel sont en acier, ce qui leur confère une grande raideur (E=3 1011 N/m2). Son registre se situe donc dans l'aigu, typiquement de sol5 (784 Hz) à do8 (4186 Hz). Même pour la note la plus basse (784 Hz), les partiels (2161 Hz, 4240 Hz, etc) se situent déjà dans une zone où l'oreille est moins sensible. Il en résulte un timbre métallique peu avantageux qu'on n'a pas cherché à corriger. Ceci confine l'instrument dans des effets spéciaux : le glockenspiel est très présent dans l'oeuvre pédagogique de Carl Orff et Gunild Keetman (Orff-Schulwerk, 4 extraits), à l'usage des enfants et, au concert, on ne le rencontre que très rarement, par exemple dans un épisode célèbre de la Flûte enchantée de Mozart (en 2:21).
- Les lames du xylophones sont en bois (exotique) comme le nom l'indique. Il existe des variantes modernes en matériaux synthétiques et même en métal - dont les jouets de votre enfance - mais parler de xylophone dans ce cas est clairement un abus de langage. Le module d'Young, E, du bois étant inférieur d'un ordre décimal environ à celui de l'acier, cela a pour effet d'abaisser le registre de l'instrument qui s'étend normalement du fa4 (349 Hz) au do8 (4186 Hz). Le xylophone peut faire partie de l'orchestre symphonique, la brillance et la puissance de sa sonorité le permettent, mais il s'y trouve généralement confiné dans les effets pittoresques tels ceux que Saint-Saëns a prévus pour Le Carnaval des Animaux, dans l'épisode n° 12 des Fossiles.
- Le marimba est pour faire simple un xylophone (d'origine africaine et qui a transité par l'Amérique du Sud), muni de tuyaux résonants, un par lame. Les commentateurs de tous bords entretiennent une certaine confusion entre xylophone et marimba. Par exemple, on a prétendu les distinguer par l'absence de résonateur dans le cas du xylophone ce qui n'a jamais été le cas du marimba mais aujourd'hui le xylophone profite pleinement de ce progrès évident. Actuellement, les différences parfaitement audibles qui subsistent entre ces deux instruments concernent leur accordage (Cf ci-après). Le registre d'un grand marimba de concert s'étend habituellement du la2 (110 Hz) au do7 (2093 Hz) mais il peut descendre jusqu'au do2 (65 Hz).
La différence de sonorité entre un xylophone et un marimba est le point le plus intéressant à discuter. La théorie des barres à section droite nous apprend que les deux premiers partiels, f1 et f2 = 2.76 f1, sont distants de 1200 ℓg(2.76) = 1755.5 cents, soit un peu moins que 3/2 octave. Cela est vrai pour un xylophone comme pour un marimba, tous paramètres physiques égaux. Le fait que 2.76 ne soit pas un nombre entier signe évidemment l'inharmonicité de la lame d'où l'idée de la corriger. On y parvient en creusant la face inférieure des lames selon un profil d'allure parabolique concave. Enlever de la matière à une lame revient à en diminuer l'épaisseur, d'où un abaissement des fréquences partielles, fn (variable selon n). Cette opération affectant séparément f1 et f2 (sans oublier celles qui suivent), le rapport f2/f1 peut, en creusant bien, être ajusté à la valeur 3 (ce qui positionne le deuxième partiel à la quinte de l'octave du premier, cas du xylophone) ou à la valeur 4 (c'est alors à l'octave de l'octave, cas du marimba mais aussi du vibraphone).
Note. Cette manoeuvre a une conséquence indirecte sur la largeur des lames du marimba. En principe, cette largeur n'intervient pas dans le calcul du spectre des fréquences d'une lame parallélépipédique, d'où les lames pourraient être de largeurs égales. Toutefois, lorsqu'on évide les lames, cela cesse d'être rigoureusement vrai d'où une correction s'impose à ce stade. On pourrait décider de la faire empiriquement (à l'oreille) en modifiant légèrement la longueur des lames mais le résultat ne serait pas globalement esthétique. On préfère élargir insensiblement la largeur des lames à mesure qu'on s'enfonce dans le grave, ce qui donne un clavier progressif.
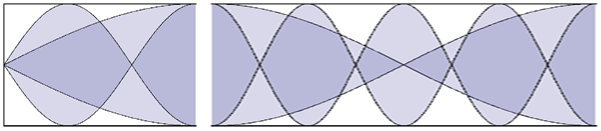
Les modes variés d'accordage conditionnent les types de résonateurs attachés aux lames des deux instruments :
- Un tuyau de bonne longueur, ouvert à une extrémité et fermé à l'autre, fait résonner une fréquence et ses multiples impairs, donc f1, 3f1, 5f1, etc mais pas 4f1. Un tuyau de ce type convient donc au xylophone puisque celui-ci s'accorde sur le principe f2 = 3f1. Par contre, il ne convient pas au marimba.
- Un tuyau de bonne longueur, ouvert à ses deux extrémités, fait résonner une fréquence et tous ses multiples, donc f1, 2f1, 3f1, 4f1, etc. Il convient donc au marimba puisqu'il fait résonner simultanément f1 et 4f1 (Il conviendrait aussi au xylophone mais il serait inutilement long). Malheureusement il est de longueur double (cf figure ci-dessus à droite), d'où on préfère éventuellement une variante plus compliquée où une valve réglable modifie l'ouverture d'un tuyau semi-ouvert.
L'accord du deuxième partiel à la double octave de la fondamentale est confortable pour l'oreille : il favorise une meilleure perception de la hauteur de la note visée. Ce n'est pas tout : le timbre de l'instrument gagne encore à ce qu'on se préoccupe de l'accord du troisième partiel, que l'on ajuste en pratiquant des entailles supplémentaires dans la partie non encore évidée de la lame. Tous ces raffinements confère au marimba un son nettement moelleux par rapport au xylophone qui sonne plus agressivement (En Europe, il arrive qu'on accorde le xylophone comme le marimba (selon, f2 = 4f1) mais sans extension aux partiels suivants).
Les trésors d'inventivité qu'on a déployés autour du marimba ont été récompensés par une sonorité veloutée unique en son genre. Malheureusement le répertoire consacré à cet instrument tardif est fatalement mince : on dénombre quelques concertos écrits au 20ème siècle et de rares oeuvres dédicacées. Les virtuoses de l'instrument sont dès lors contraints de recourir à des transcriptions dont J-S Bach fait inévitablement les frais, heureusement sa musique résiste à tout. Parmi les compositeurs actuels, Steve Reich s'est intéressé de près aux possibilités de l'instrument dans quelques oeuvres devenues célèbres (Sextuor pour 6 (!) marimbas, Nagoya Marimbas et surtout la mythique Music for Mallets Instruments). Bright Sheng (1955- ) s'est également laissé tenter dans Deep Red mais, curieusement, ce sont des compositeurs peu connus qui se tirent le mieux d'affaire, tels Alejandro Vinao (1951- ) dans Arabesco infinito pour marimba et vibraphone et Alice Gomez (1960- ) dans Gitano, une très belle oeuvre que Yumiko Noto joue sur un instrument somptueux.
Vibrations de la corde raide
L'inharmonicité et ses problèmes d'accordage ne concernent pas que les instruments idiophones, elle apparaît également dans la théorie d'un instrument aussi fondamental que le piano moderne (Hammerklavier).
Rappelons qu'une corde dépourvue de raideur garde la forme qu'on lui donne en toutes circonstances. Une corde raide exige un effort pour être courbée. Si on la dépose sur une table dans cet état, elle réagit sous l'effet de tensions internes et elle tend à reprendre la forme de repos qui minimise ces tensions. Comme pour les lames, la grandeur physique qui quantifie la raideur d'une corde est son module d'Young, E. Voyons comment elle influence les modes de vibration des cordes raides.
Alors que la corde idéale est supposée infiniment fine, la corde raide possède une structure, disons cylindrique, dont le rayon, r, cesse d'être négligeable. Elle se situe entre les cas extrêmes étudiés ci-avant de la corde idéale et de la lame vibrante. La théorie qui décrit sa vibration repose sur une équation de propagation qui combine les dérivées spatiales d'ordre deux et quatre telles qu'elles apparaissaient dans l'étude des cas séparés (T demeure la tension, E le module d'Young, S = π r2/4 la (surface de) section, μ = ρS, la masse linéique et g vaut à nouveau r/2 dans le cas d'une corde cylindrique de rayon, r). Cette équation se note : ∂ttu(x,t) - c2 ∂xxu(x,t) + κ2 ∂xxxxu(x,t) = 0, où l'on pose cette fois : c2 = T/μ, κ2 = E r2/(4 ρ) et ωn = 2πfn. Sa solution générale s'écrit :
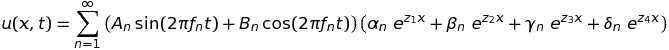
Dans cette expression, les zi (i=1, 2, 3, 4) sont solutions de l'équation quartique, κ2 z4 - c2 z2 - ω2 = 0. A ce stade, il y a lieu de prendre en compte les 4 conditions aux limites, u(0,t) = u(L,t) = u''(0,t) = u''(L,t) = 0. Celles en x=0 imposent, βn = -αn et δn = -γn, et celles en x= L déterminent les fréquences autorisées, fn, comme suit :
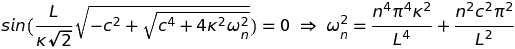
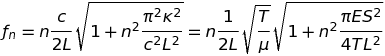
Cette dernière formule doit être comparée à celle obtenue antérieurement pour la corde idéale (Pour rappel : fn = n/(2L) ✓(T/μ)). On constate qu'elles diffèrent par le facteur correctif, n2πE S2/(4T L2), qui signe précisément l'inharmonicité de la corde raide. Plus ce facteur est appréciable par rapport à 1 (en pratique, à partir de 0.01) plus la corde est inharmonique. Les paramètres physiques, E, S, T et L, influent tous à leur manière sur le degré d'inharmonicité : celui-ci diminue soit lorsque E et/ou S diminuent soit lorsque T ou L augmentent (et inversement). Parvenu à ce stade, on pourrait penser faire un sort à l'inharmonicité en n'utilisant que des cordes longues et fines mais ce n'est pas toujours possible, en particulier dans le cas du piano, qui met ses cordes à rude épreuve en les frappant violemment pour garantir un son puissant. Ce problème est au centre du cordage et de l'accordage de cet instrument.
Le piano fait de la corde raide
Le modèle de la corde idéale convient bien aux instruments de la famille du violon, il ne convient pas au piano. Celui-ci repose sur le modèle de la corde raide dont les fréquences propres sont données par la formule connue, réarrangée et particularisée au partiel fondamental, n=1 :
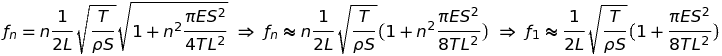
C'est la correction d'inharmonicité, 0.4 ES2/(TL2) qui est au centre de la discussion qui suit.
Le clavier d'un piano moderne usuel comporte 88 touches couvrant un peu plus que 7 octaves, allant du la0 (27.5 Hz) au do8 (4186 Hz). Cela n'a pas toujours été le cas : au 18ème siècle il n'en comportait que 54 puis 60. Plus récemment, on a aussi construit des claviers plus étendus, descendant jusqu'au do0 (16 Hz). Plusieurs compositeurs du 20ème siècle ont exploité des notes très graves (Ferruccio Busoni dans ses transcriptions d’œuvres pour orgue de Bach, Maurice Ravel dans quelques pièces célèbres, Bela Bartok, dans son Concerto n°2). A l'inverse, on a construit des claviers montant plutôt inutilement jusqu'au fa8 (5588 Hz). Scriabine, en particulier, a noté un ré8 (4699 Hz) dans sa Sonate n°6.
Les cordes en acier ne rayonnant pas avec une intensité suffisamment uniforme en fonction de leurs caractéristiques physiques, on est amené à en dédoubler voire détripler certaines. Au bilan, un piano ne comporte pas 88 cordes mais nettement plus, jusqu'à 243, par exemple selon le schéma suivant, en progressant du grave vers l'aigu : 8 monocordes filées (par un enroulement simple ou double, cf infra), 5 bicordes filées, 7 tricordes filées et 68 tricordes non filées. Le filage consiste à enrouler un fin fil de cuivre autour d'une corde centrale pour en augmenter la section sans en augmenter la raideur dans des proportions comparables : cela atténue l'inharmonicité sans altérer la fréquence. Cette manoeuvre est utile mais elle fragilise la corde centrale, d'où la nécessité de choisir celle-ci en acier résistant (Des valeurs typiques pour ce genre de cordes sont E = 3 1011 N/m2 et ρ = 7800 kg/m3).
Toutes ces complications résultent de la volonté de couvrir un spectre fréquentiel large au moyen d'un ensemble de cordes tenant dans un espace raisonnablement limité. Il n'est, en effet, pas envisageable de diversifier les 88 cordes du piano sur base de leur seule longueur. En maintenant égaux tous les autres paramètres physiques (E, ρ, S et T), le rapport des longueurs correspondant aux notes extrêmes vaudrait, 4186/27.5 ≈ 152.2. Etant donné que la corde la plus aiguë peut difficilement descendre en-dessous de 5 cm, cela obligerait la corde la plus grave à approcher les 8 m, ce qui est inconcevable non seulement à cause de la place que l'instrument occuperait mais aussi parce que des cordes aussi longues vibreraient avec une amplitude telle qu'elles s'entrechoqueraient ! La solution consiste évidemment à jouer sur les autres paramètres.

On joue peu sur la tension des cordes car il convient de ne pas déséquilibrer le cadre (en fonte si vous mettez le prix !), qui doit résister à des efforts considérables. La tension suffisante pour assurer une intensité sonore convenable varie en progression continue, de 600 N, dans l'aigu, à 750-1000 N dans l'extrême grave. Au total, le cadre doit allègrement supporter un effort avoisinant les 200000 N, l'équivalent d'un poids de 20 Tonnes !
Les cordes aiguës sont les plus minces, de l'ordre de 0.7 mm d'épaisseur, puis celle-ci augmente pour atteindre environ 1.4 mm dans le medium. Les cordes graves sont encore plus épaisses afin d'en accroître la masse linéique. Bien qu'aucune formule théorique ne l'impose (Les dimensions modestes des épinettes le prouvent !), les facteurs ont privilégié une longueur minimum pour les cordes de piano afin de garantir une intensité sonore suffisante dans le médium. Les valeurs numériques qui sont mentionnées dans la suite ne sont fournies qu'à titre indicatif, pour fixer les idées. De fait, sauf évidemment pour les instruments produits en série (sans parler des instruments historiques), il n'y a pas deux pianos accordés physiquement de la même façon, d'où il n'existe aucune table universelle fixant les paramètres physiques de chaque corde.
Les (multi-)cordes sont astreintes à passer sur un chevalet en bois dur (hêtre ou érable) sur lequel elles exercent chacune un effort de l'ordre de 10-20 N, transmis à la table d'harmonie qui joue le rôle de caisse résonante. Comme il a été dit en introduction, les dimensions conférées à l'instrument donc à sa table ne permettent pas à celle-ci de résonner aux fréquences les plus basses. Les notes les plus graves sont donc privées de leur composante fondamentale (même le partiel, n = 2, n'est pas très présent), ce qui n'empêche pas que nous la "ressentions" (Cf infra, les mécanismes de l'audition).
Il existe deux chevalets, bien visibles sur la figure ci-dessus : l'un pour la vingtaine de notes les plus graves et l'autre pour les notes restantes. Les cordes graves passent pardessus les autres en les croisant, ce qui contribue à améliorer l'équilibre global du cadre. Toutes ces subtilités compliquent la vie des facteurs et des accordeurs de piano. A leur sujet, il ne faut pas confondre cordage et accordage :
- Le plan de cordage est de la responsabilité du facteur qui conçoit l'instrument : il doit estimer par le calcul les caractéristiques physiques de chaque groupe de cordes (Choix du matériau, longueur, section, tension, etc) et affiner les réglages en faisant appel à son expérience. La réussite de l'entreprise tient, pour beaucoup, à la régularité de la progression du son, en particulier de l'inharmonicité, d'une corde à la suivante. Or les motifs de discontinuités sont nombreux : cordes de longueurs variables, simples, doubles ou triples, filées ou non, transitant par un chevalet ou par l'autre. Pour compliquer le tout, il faut garantir un maximum d'homogénéité dans l'intensité sonore des divers registres, ce qui nécessite de bien choisir le diamètre des cordes (centrales) et de régler précisément leurs tensions. Lorsque le cordage est achevé, il devient difficile de revenir en arrière : s'il est déficient, autant recommencer à zéro.
- Accorder l'instrument est de la compétence de l'accordeur. Il doit vérifier que les paramètres du cordage primitif sont toujours en place et faire le choix d'un tempérament convenable. On règle souvent ce problème un peu vite en affirmant que le piano est, par essence, accordé au tempérament égal mais ce n'est pas rigoureusement exact. Le problème est très apparent dans le registre aigu : la fréquence fondamentale, f1 = (1/2L)✓(T/ρS), est élevée si la tension est élevée et si la section est faible, deux contraintes qui vont dans le sens d'une fragilisation de la corde. La parade envisageable est de raccourcir la corde mais cela augmente l'inharmonicité, B = 0.4 ES2/(TL2). Considérons la note la plus aiguë, de fréquence, f1 = 4186 Hz : sa corde mesure, L = 0.05 m, elle supporte une tension de, T = 600 N, et sa section, S = 4.4 10-7 m2, correspond à un diamètre de l'ordre de 0.75 mm. On en déduit un facteur d'inharmonicité, B = 0.015, trop important pour être négligé, voyons pourquoi.
L'un des principes directeurs de l'accordage est de faire coïncider le deuxième partiel d'une note donnée avec le premier partiel (le fondamental) de la note située une octave plus haut. En l'absence d'inharmonicité, cela serait automatiquement garanti par le tempérament égal mais ce n'est plus vrai en présence d'une inharmonicité qui décale le deuxième partiel de la note donnée vers le haut. Illustrons ce point sur le couple do7-do8 : en tempérament strictement égal, il suffit de garantir un rapport des fréquences égal à 2 soit 2093 Hz et 4186 Hz. Cependant si le do7 est frappé d'une inharmonicité de l'ordre de B = 0.015, son deuxième partiel ne se situe plus à 4186 Hz mais un peu plus haut, à 4186 × 1.015 = 4248.8 Hz. Pour éviter tout battement parasite, il convient dès lors de déplacer le do8 de 1200ℓg(1.015) = 25.8 cents, soit un huitième de ton, c'est le principe de l'accordage par dilatation d'octave.
L'inharmonicité se calcule de la même façon dans le registre medium (do4 = 261.6 Hz) mais on l'y trouve négligeable, de l'ordre de 0.002, ce qui a pour conséquence que le tempérament égal reprend ses droits.
Une méthodologie globale se dégage, à ce stade, qui consiste à accorder le registre medium au tempérament strictement égal puis à dilater progressivement et de plus en plus les octaves aiguës. Un dilemme apparaît cependant si l'on se préoccupe d'ajuster, en plus, le partiel n°4 d'une note donnée à la fondamentale de la note doublement octaviée : on trouverait qu'il faut dilater les octaves autrement qu'on ne l'a déjà fait. On comprend que face à de telles contradictions, l'accordeur a intérêt à trancher en se fiant à sa qualité d'écoute.
La situation est plus délicate dans le registre grave. A première vue, on serait tenté d'extrapoler au registre grave les calculs effectués dans l'aigu et le medium. Si on le fait, on trouve une inharmonicité négligeable, inférieure à 0.001. Cela n'est vrai que si tous les paramètres physiques sont extrapolés sans tricher, en particulier si la longueur des cordes graves tend vers 8 m. Ce n'est évidemment pas le cas et pour la ramener vers 2 m, force est d'augmenter la section de ces cordes. Si l'on recommence les calculs sur cette base, à propos du la0 (= 27.5 Hz), on trouve une valeur encore fort raisonnable, de l'ordre de, B = 0.0027, à peine plus dérangeante que celle trouvée dans le medium. Une subtilité peut intervenir, à ce stade, liée au phénomène déjà évoqué du fondamental manquant. L'accordage devant se faire entre le deuxième partiel (n = 2) et la fondamentale située deux octaves plus haut, le facteur d'inharmonicité est multiplié par n2 = 4, ce qui le déplace dans la zone critique, B ≈ 0.01.
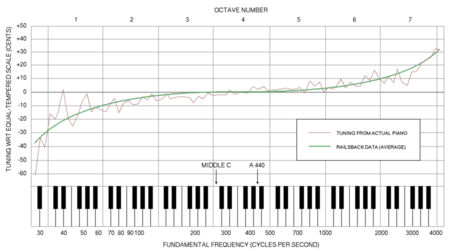
En extrême résumé, l'inharmonicité des cordes aiguës résulte de ce qu'elles doivent être minces, fortement tendues et courtes pour ne pas se rompre et celle des cordes graves résulte d'un plan de cordage tendant à limiter leur longueur bien en-dessous des 8m théoriques, ce qui implique une compensation soit en abaissant la tension ou en augmentant la section (ou les deux); dans les deux cas la manoeuvre aggrave l'inharmonicité. En pratique, on commence par accorder un piano dans le registre medium en respectant le tempérament égal, puis on étend l'accordage aux registres extrêmes en dilatant progressivement les octaves, ce qui a pour effet de rendre chaque note aiguë (resp. grave) progressivement plus aiguë (resp. grave) qu'elle ne le serait au tempérament strictement égal. Ce phénomène de dilatation d'octave qui peut atteindre 34 cents (soit 1/6 de ton) est clairement visible sur la courbe expérimentale de Railsback (The Journal of the Acoustical Society of America 9, pp 274 (1938)).
La perception du son.
1. Anatomie de l'oreille
Tout écolier a étudié une fois dans sa vie une description anatomique de l'oreille humaine. Il a appris et peut-être retenu les rudiments suivants :
- Le pavillon externe focalise l'onde de pression vers le conduit auditif.
- Le conduit auditif, de longueur approximative, L = 2.5 cm, joue le rôle de guide d'onde, ouvert à une extrémité (côté pavillon) et fermé à l'autre (côté tympan). Il favorise les fréquences proches de, fn = n c/(4L) = n 3400 Hz, au niveau du tympan.
- Le tympan est une membrane fibreuse inhomogène, de forme vaguement elliptique (section oblique, S ≈ 60 mm2), d'épaisseur variable (e ≈ 0.1 mm) et de raideur, E ≈ 2 107 N/m2. Dès qu'il est frappé par l'onde sonore, il entre en vibration mais tellement loin de la résonance (Cf introduction) que l'amplitude de son mouvement demeure très faible, de l'ordre de 0.3 μm. Le tympan est l'interface air-air qui sépare les oreilles externe et moyenne. Tout mouvement tympanique modifie la pression dans l'oreille moyenne et c'est le rôle de la trompe d'Eustache (du nom de Bartolomeo Eustachi qui fut le premier à la décrire, en 1543) d'équilibrer cette pression à la valeur atmosphérique.
- La faiblesse du mouvement tympanique exige des mécanismes de compensation. La chaîne tarabiscotée des osselets (dans l'ordre, marteau, enclume et étrier) agit précisément comme un système de leviers sur la fenêtre ovale afin d'en amplifier la vibration.
- La fenêtre ovale est l'interface air-liquide séparant les oreilles moyenne et interne. Le grand rapport (≈ 820) de densité des milieux lui fait jouer le rôle de presse hydraulique amplifiant à nouveau les vibrations dans l'oreille interne. Elle est la fenêtre d'entrée sur le vestibule qui donne sur la cochlée (prononcez "cocklée").
- La cochlée est communément appelée limaçon (escargot aurait été plus juste) du fait qu'elle est enroulée sur elle-même autour d'un axe osseux en faisant 2¼ tours. D'un haut degré de sophistication, elle est l'organe essentiel de l'audition, celui qui permet une discrimination des sons en intensité (entre 0 et 120 dB) et en fréquence (entre 16 et 16000 Hz). L'exposé du principe de son fonctionnement passe par une description anatomique préalable, ci-après simplifiée à l'extrême. Si vous voulez tous les détails, faites un Voyage au Centre de l'audition (Rémy Pujol, INSERM Montpellier).
2. La cochlée comme analyseur fréquentiel
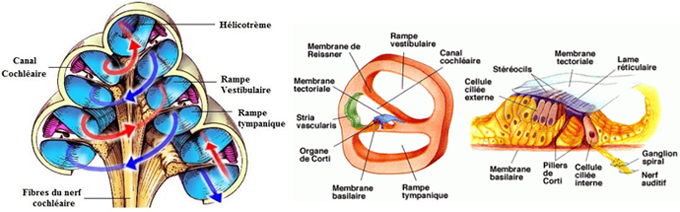
La cochlée est constituée de trois canalicules, la rampe vestibulaire, la rampe tympanique et le canal cochléaire, séparés par les membranes tectoriale et basilaire. Lorsque l'étrier frappe la fenêtre ovale, il envoie une onde de pression longitudinale dans la périlymphe qui baigne le canal d'entrée (Sur la figure ci-dessus, à gauche, suivez les flèches rouges qui parcourent la rampe vestibulaire). Cette onde se propage de la base de la cochlée vers son sommet (l'apex), elle passe par l'ouverture de l'hélicotrème et fait le chemin inverse via le canal parallèle de sortie (Sur la figure ci-dessus, à gauche, suivez les flèches bleues qui parcourent la rampe tympanique). Elle aboutit à la fenêtre ronde qui joue un rôle d'amortisseur.
La figure du milieu présente une coupe transversale du canal cochléaire, coincé entre les deux rampes. Toute vibration intense en un point des rampes est transmise au point correspondant dans l'endolymphe du canal cochléaire et donc à l'organe de Corti qui y loge. La membrane de celui-ci est tapissée par quelques milliers de cellules ciliées (CC), chargées de détecter le passage de l'onde et de l'analyser tant en fréquence qu'en intensité.
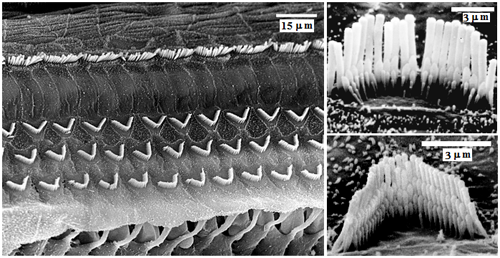
Il en existe de deux sortes : environ 3500 cellules ciliées internes (CCI) et 12000 cellules ciliées externes (CCE) facilement reconnaissables sur le cliché ci-dessous, pris au microscope électronique à balayage. Elles sont alignées parallèlement : une rangée de CCI alignées et trois rangées de CCE disposées en W. Le diamètre des cils est constant, de l'ordre de 7 μm, mais les longueurs des CCE varient selon leur position dans la cochlée : de 25 μm à la base elle passe à 70 μm à l'apex, ce point aura son importance lorsque nous discuterons le mécanisme de discrimination en fréquence. Ces cellules sont constituées dès les deux premiers mois de la gestation humaine; elles sont précieuses, protégez vos oreilles car elles ne se renouvellent pas !
Voyons, à présent, comment s'opère la reconnaissance des hauteurs de sons. Nous avons signalé, en introduction, que le mécanisme imaginé par Helmholtz, un système de cordes telles celles d'une harpe, entrant en résonance sélective, sans être absurde, ne convient pas vraiment. Les CC présentes le long de la membrane basilaire pourraient a priori jouer le rôle imaginé par Helmholtz mais les valeurs de leurs paramètres physiques les éloigneraient tellement de la résonance qu'il en résulterait un pouvoir de discrimination bien trop faible comparé à celui qu'on observe.
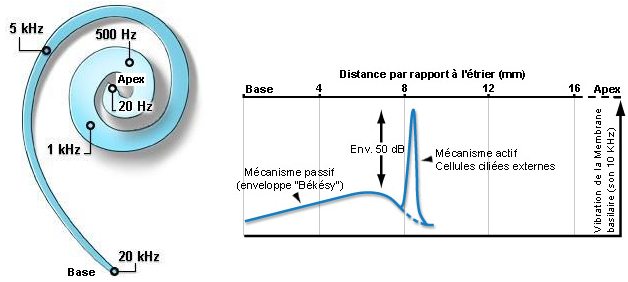
En 1961, le physiologiste hongrois, Georg Von Békésy (1899-1972), a reçu le Prix Nobel de médecine pour une interprétation déjà plus proche de la réalité. C'est en travaillant sur des simulations hydrauliques qu'il a imaginé le protocole suivant : c'est un fait anatomique qu'en partant de la base de la cochlée et en se dirigeant vers son sommet, la membrane basilaire s'élargit tandis qu'elle perd en raideur. Ces deux facteurs agissent dans un même sens lorsque l'étrier frappe à la fenêtre ovale, chassant la périlymphe vers la rampe vestibulaire : une onde de fréquence basse a tendance à atteindre son pic d'intensité au sommet de la cochlée, là où l'espace disponible est maximum et la rigidité moindre tandis qu'une onde de fréquence haute a tendance à se concentrer à la base de la cochlée. Pour une onde de fréquence intermédiaire, le pic d'intensité est atteint entre ces extrêmes. Seules les CCI proches du pic d'intensité vibrent suffisamment pour ouvrir des canaux ioniques et enclencher une cascade de mécanismes électrochimiques par échanges d'ions (K+, Na+ et Ca++). Les détails importent peu, il suffit d'imaginer que ces échanges (dé)polarisent les cellules ciliées et génèrent un influx nerveux à destination du cortex cérébral. Pour un son de fréquence unique, seuls sont excités les cils situés au voisinage immédiat du site concerné par le pic d'intensité. Pour un son complexe, chaque composante excite la population de cils concernés et c'est l'ensemble des excitations électriques qui est acheminé vers le cortex cérébral aux fins d'interprétation.
Le point faible du modèle de Von Békésy, connu sous le nom de tonotopie passive, est qu'il ne rend pas parfaitement compte du haut pouvoir de discrimination de l'oreille en fréquence. Il a été perfectionné, vers la fin des années 1960, par plusieurs chercheurs, notamment, T. Gold, B. M. Johnstone et A. J. Boyle. Tirant parti du fait que les CCE proches de la base de la cochlée sont plutôt courts et raides alors que ceux situés près du sommet sont plutôt longs et souples, ils ont émis l'hypothèse que l'activité électrique déclenchée au niveau des CCE a pour effet rétroactif de renforcer ces différences physiques, on parle de tonotopie active. Ceci contribue à augmenter de 50 dB (un facteur 100000 !) la sensibilité des cils dans leurs domaines fréquentiels spécifiques, c'est un peu l'hypothèse primitive de Helmholtz qui refait surface.
On a pu ainsi préciser une cartographie en fréquences du chemin complet de la membrane cochléaire fonctionnant comme un analyseur fréquentiel.
Pour conclure cette incursion en physiologie, il peut être utile d'insister sur le fait que ce que nous entendons n'est pas ce que les instruments de laboratoire mesurent et d'ailleurs, la comparaison est passablement vide de sens. Les caractéristiques de l'onde de pression peuvent être analysées par un oscilloscope : il suffit d'enregistrer le son au moyen d'un microphone fidèle et de faire apparaître le signal électrique capté à l'écran. Personne ne doute raisonnablement que son graphe est une copie conforme du graphe de l'évolution en pression car il est admis qu'avec un microphone digne de ce nom, la transduction pression-courant se fait sans distorsion. L'oreille procède différemment : elle traite l'onde sonore en échantillonnant ses paramètres de fréquence et d'intensité et en les transcodant sous la forme d'un signal bioélectrique destiné au cerveau. Il n'est nullement garanti que celui-ci coïncide avec l'original car dans le processus invoqué, c'est la chimie de mécanismes ioniques qui est à l'oeuvre. Cette coïncidence n'est d'ailleurs pas vitale car la seule chose qui importe c'est que le (dé)codage se fasse de façon suffisamment stable pour garantir qu'un même auditeur (sain) entende toujours la même chose lorsque le son se répète à l'identique. Si le cerveau reçoit le codage électrique anatomique d'un son grave, il en fait invariablement une interprétation qu'avec nos habitudes culturelles nous nommons "son grave", présumant - mais c'est un acte de foi - que tout le monde entend "la même chose". Vous ne connaîtrez jamais ce que votre voisin entend mais, rassurez-vous, sauf accident survenant à votre ouïe, vous entendrez toujours la même chose dans des circonstances égales. Ces considérations participent davantage de la psychoacoustique que de la biophysique aussi nous ne nous y attardons pas.
Mirages et merveilles de l'électronique
Les problèmes que l'oreille doit résoudre pour assurer les mécanismes de l'audition se retrouvent à peine déguisés dans le domaine du traitement électr(on)ique du son donc de l'enregistrement musical. En particulier, la miniaturisation galopante des microphones et des haut-parleurs questionne un parallèle avec ce qui a été dit à propos de la gestion des sons par notre appareil auditif, du tympan à la cochlée.
Tout enregistrement effectué en studio ambitionne de capturer le son au moyen de microphones et de le coder sur un support matériel aux fins d'être restitué, tôt ou tard, par des haut-parleurs; vos oreilles feront le reste si vous en avez pris soin. Le recours à l'électronique est permanent dans ce processus et la question se pose du rapport du son trafiqué à l'original.
De même qu'on s'est étonné ci-avant que le mécanisme de l'audition puisse se développer dans le cadre exigu de l'oreille interne, on s'émerveille que les microphones actuels portent de mieux en mieux leur nom, dépassant à peine la taille d'une noisette et que les haut-parleurs fassent à peine moins bien pour ne pas encombrer nos salons exigus.
Pourtant, lorsqu'on capte et retransmet un coup de la grande timbale déjà évoquée en introduction, de diamètre 82 cm, on se demande bien comment les petits haut-parleurs vont se débrouiller pour nous faire entendre un do2 (65.4 Hz). Ceci demande quelques mots d'explication.
Précisons d'emblée que les considérations qui suivent ne concernent pas les haut-parleurs de pacotille qui équipent les autoradios ou les postes dits à transistors : aucun n'émet les partiels graves que l'on attend éventuellement car ils sont tous manquants. Nous avons vu que dans ces cas, notre appareil auditif fait de son mieux pour nous donner l'illusion de leur présence au point que roulant seul dans une nuit noire, la Symphonie Pastorale peut garder une part de sa magie éternelle.
Les haut-parleurs s(er)ont toujours le maillon faible d'une chaîne dite de haute-fidélité. Leur membrane vibrante, disons, pour faire simple, de rayon R, d'épaisseur, e, de masse volumique, ρ et soumise à une tension (mécanique) périphérique par unité de longueur, σ, ne peut en aucun cas suivre le modèle théorique de la timbale, fixée fermement tout le long de son périmètre. Si c'était le cas, les conditions aux limites interdiraient toute vibration de fréquence située en-dessous d'un seuil très supérieur à 16 Hz. Les calculs théoriques montrent, en effet, que les fréquences propres d'une membrane contrainte sont données par la relation suivante, où les αm,n sont les zéros des fonctions de Bessel (Jm(αm,n) = 0, m=0, 1, 2,... et n =1, 2, 3,..., le plus bas valant, α0,1 ≈ 2.40483) :
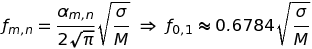
Pour abaisser la fréquence de seuil, f0,1, d'une membrane contrainte, il faut augmenter sa masse, M, et diminuer la raideur (σ) de sa suspension, ce qui revient à l'affranchir de conditions aux limites contraignantes. Il en résulte qu'une membrane unique n'est généralement pas en mesure d'assurer la reproduction de toutes les fréquences du spectre audible : il faut prévoir des membranes distinctes pour couvrir les plages fréquentielles graves ((sub)woofer), medium et aiguës (tweeter). Les membranes graves pêchant par manque de puissance, une amplification électronique s'avère nécessaire pour faire en douceur les raccordements qui s'imposent.
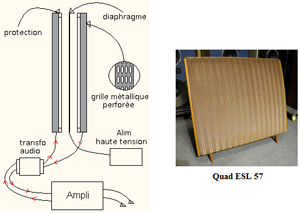
Ces remarques (très) générales concernent les haut-parleurs électrodynamiques, de loin les plus fréquents, mais sachez qu'il existe une alternative qui nous rapproche davantage de l'idéal inaccessible : le haut-parleur électrostatique utilise une membrane conductrice suspendue (chargée sous haute tension continue par une alimentation externe), de grande dimension (pouvant approcher et même dépasser le m2), entraînée à vibrer dans le champ électrique créé par deux électrodes parallèles alimentées par le signal audio. Sa dimension et le fait qu'elle vibre quasiment d'un seul tenant règlent naturellement le problème des basses fréquences. Cette solution extraordinairement élégante et sans doute inégalable, sur le papier autant qu'à l'oreille, est malheureusement onéreuse, fragile, sujette aux variations météorologiques (humidité) et ... encombrante surtout qu'on ne peut pas disposer les enceintes n'importe comment, on tente de se rapprocher de l'acoustique de salle ! N'hésitez pas à visiter un salon qui propose ce genre de haut-parleurs en démonstration, vous entendrez la différence, en particulier sans fatigue auditive ! Très peu de constructeurs ont investi ce domaine de recherche, le modèle pionnier, exposé ci-contre, est celui de ma jeunesse mais il a été remplacé par des modèles plus récents.
Le microphone n'est jamais qu'un haut-parleur fonctionnant à l'envers. Il en existe de beaucoup de sortes mais les plus fréquents sont à bobine mobile, collée à la membrane vibrante. Comme pour les haut-parleurs, celle-ci doit être suspendue et certainement pas fixée fermement. Comme le tympan, elle ne vibre que faiblement car elle est loin de la résonance. Une amplification électronique est dès lors nécessaire. Dans le cas du tympan elle reste modérée car le cerveau n'a pas besoin de recevoir un signal intense pour déclencher une réponse auditive. En comparaison, le microphone exige une amplification d'autant plus importante qu'il s'agira in fine d'alimenter des haut-parleurs réputés de faible rendement lorsqu'ils sont fidèles.
De même qu'il existe des haut-parleurs électrostatiques il existe des microphones fonctionnant sur le même principe : une surface mobile recouverte d'une couche conductrice est disposée parallèlement à une surface fixe avec laquelle elle fait condensateur plan, de capacité, C = εS/d. Toute vibration de la surface mobile modifie la distance, d, donc la capacité du condensateur. Les surfaces sont porteuses d'une charge, Q = CV, desservie par une alimentation extérieure (dite fantôme), de tension continue, V. Lorsque le micro entre en activité, la membrane se déplace sous l'effet de l'onde de pression, faisant varier la distance, d, donc aussi la capacité, C. Comme la charge est constante, c'est la tension entre les armatures qui varie, selon la loi, V = Qd/(ε S), fidèle à la pression de l'onde. Une amplification de V est cependant nécessaire pour alimenter les haut-parleurs.
Bien que tout enregistrement représente une mise en boîte musicale, nul n'en conteste l'utilité car lui seul permet l'accès à tous les répertoires disponibles. Quant à parler de haute-fidélité, tout dépend de quelle hauteur on parle. Les accrocs aux écouteurs justifient leur pratique en faisant remarquer qu'il ne s'agit après tout que d'un (dé)codage de plus comme il y en a déjà tant, du tympan au cerveau. Les autres rétorquent que même les yeux bandés, jamais ils ne confondront le son direct, vécu en salle, et le son manipulé, même avec le plus grand soin. Ceci pose le problème plus vaste d'une véritable diététique acoustique mais, chut, ce sera pour une autre fois (Cf Musique et Art culinaire).