Faits divers
Modalité musicale et arithmétique modulaire
Sommaire
[ afficher ]- Construction d'une gamme primitive
- La gamme pythagoricienne
- Le mode ionien
- Les autres modes anciens
- La dérive hellénistique
- La gamme zarlinienne
- L'émergence de la tonalité
- Comment sonnent les modes anciens ?
- La gamme chromatique à 12 sons
- Les modes de la gamme chromatique à 12 sons
- Les modes à transpositions limitées
- Le mode 2048 : l'atonalité dodécaphonique
Le langage musical occidental repose sur une tradition écrite qui appelle un alphabet (fini) ainsi qu'une syntaxe et une grammaire adaptées aux lois de l'acoustique. A cet effet, deux questions demandent à être réglées préalablement, relatives à la construction d'une gamme primitive et de son découpage éventuel en modes :
- Il convient de sélectionner un ensemble (fini) de fréquences sonores utiles (les notes) parmi l'infinité des fréquences audibles entre 16 Hz et 16000 Hz. Autrement dit, il faut construire une échelle sonore finie et discrète. Une échelle continue ne conviendrait pas pour deux raisons : une infinité non dénombrable de notes ne pourrait pas être notée à l'aide d'un alphabet fini et l'accordage des instruments à sons fixes ne permettrait pas de les jouer toutes. On pourrait objecter qu'un synthétiseur électronique surmonterait ces difficultés en programmant les notes plutôt qu'en les notant mais cela nous emmènerait hors du champ de la musique acoustique.
Une propriété physi(ologi)que du son simplifie considérablement la construction d'une échelle sonore, c'est le phénomène d'octave : deux mélodies semblables jouées simultanément à une octave de distance résonnent à nos oreilles en donnant l'impression d'une fusion parfaite. Il s'en suit que pour construire une échelle complète, il suffit de définir une échelle partielle (baptisée gamme), valable au sein d'une octave particulière (peu importe laquelle), puis de la décalquer à l'identique sur les 9 octaves adjacentes (Il existe en tout 10 octaves audibles car 16000/16 ≈ 210).
Construire une gamme, c'est partitionner l'octave au moyen d'une suite d'intervalles jointifs (non nécessairement égaux), jouant le rôle de pixels sonores : les notes de la gamme ainsi définie occupent les extrémités de ces intervalles. On réutilise les noms des notes d'octave en octave, seulement flanqués d'un indice entier (par exemple, de do0 à do9) s'il y a lieu de les différencier.
On recommande habituellement de ne pas confondre l'échelle (qui s'adresse à l'étendue du spectre audible) et la gamme (qui ne concerne que l'octave) mais cette distinction inessentielle n'est pas toujours faite. - Lorsqu'un musicien compose, rien n'impose qu'il utilise toutes les notes de la gamme "primitive" à sa disposition. Il est même fréquent qu'il n'en retienne qu'un sous-ensemble "bien" choisi, constituant ce qu'on pourrait appeler une gamme "secondaire". A première vue, cette pratique semble une limitation inutile (Pourquoi se priver de toutes les notes disponibles ?) mais ne pas y recourir entraînerait l'uniformisation des "couleurs" musicales avec la conséquence fâcheuse que toutes les oeuvres finiraient par se ressembler sinon mélodiquement du moins harmoniquement. Le mode, défini comme une restriction volontaire de l'ensemble des notes disponibles, est l'un des ingrédients de cette coloration.
Opter pour un mode, c'est donc se concentrer sur une sous-suite d'intervalles conjoints partitionnant l'octave et s'y tenir. Ces intervalles gagnent sans doute à être consonants mais ce n'est pas une règle absolue surtout en musique moderne. C'est aussi attribuer une fonction harmonique à chacun des degrés de la gamme secondaire considérée (Cf infra). Par définition, la dimension d'un mode (son nombre d'intervalles donc aussi le nombre de notes de la gamme secondaire qu'il génère) est toujours inférieure ou égale à la dimension de la gamme primitive.
La construction d'une gamme primitive est un vieux problème déjà abordé, en Grèce, il y a 2500 ans. Au fil du temps, plusieurs solutions ont été proposées et, si l'on s'en tient à la musique occidentale dite classique, il en a essentiellement existé trois (Pythagoricienne, Zarlinienne et Tempérée), chacune ayant fait fortune à une époque différente de l'histoire. Vous trouverez un exposé historique détaillé dans la chronique Gammes et Tempéraments (en abrégé G&T). Sauf la définition mathématique de la notion d'intervalle reprise ci-dessous car elle est indispensable à la compréhension du texte, nous n'en reproduisons que les conclusions utiles à l'étude des modes.
Construction d'une gamme primitive
On sait que notre perception des hauteurs sonores est logarithmique d'où il est naturel de définir l'intervalle entre deux sons en respectant une loi de ce type (Cf Acoustiques musicales). L'intervalle, mesuré en cents, séparant deux sons périodiques (notes) de fréquences, f1 et f2, est dès lors défini par la formule, Int = 1200 ℓg(f2/f1), où ℓg désigne le logarithme en base 2 et où le facteur 1200 n'est présent que pour des raisons de commodité. Avec cette unité (le cent), l'intervalle d'octave (Ex. do3-do4, rapport fréquentiel 2/1) vaut exactement, O = 1200 ℓg(2/1) = 1200 cents. Deux autres intervalles importants pour la suite sont la quinte (Ex. do-sol, rapport 3/2; Q = 1200 ℓg(3/2) = 701.95 cents) et la tierce majeure (Ex. do-mi, rapport 5/4; TM = 1200 ℓg(5/4) = 386.31 cents).
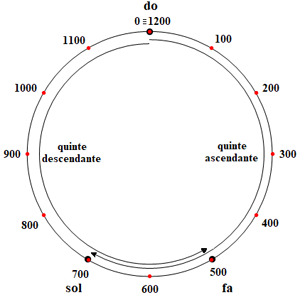
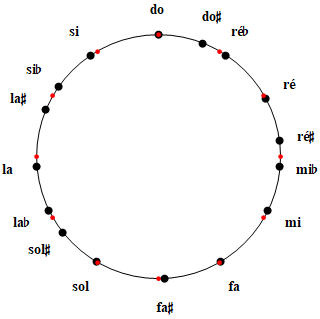
La représentation modulaire est particulièrement utile : un cercle complet représente l'intervalle d'octave (1200 cents) au départ d'une note baptisée "do", située au sommet pour davantage de lisibilité. Afin de faciliter les repérages, le cercle est gradué en 12 parties égales de 100 cents chacune (Les points rouges équidistants sur la figure ci-contre). On positionne les notes appartenant à une octave commune sur le périmètre du cercle en respectent les valeurs des intervalles les séparant du do initial. Un saut d'octave entre deux notes, Ni et Ni+1, correspond à une progression de 1200 cents sur le périmètre ou, ce qui revient au même, à une rotation de 360° au départ de la note Ni. La rotation se fait dans le sens horlogique si l'intervalle est ascendant et dans le sens inverse s'il est descendant. On représente de même un saut de quinte en progressant de 701.95 cents (approximativement 7 intervalles marqués par les repères rouges) ou, ce qui revient au même, en effectuant une rotation de 210° 35' 12". Dans tous les cas, deux notes distantes d'une octave, Ni et Ni+1, sont représentées par un même point sur le cercle, c'est le principe de la représentation modulaire, analogue à celle qui se pratique sur le cadran d'une montre à aiguilles. En arithmétique modulaire (modulo 1200), 100+100=200 mais 600+600=0 et 700+700=200 car à partir de 1200 (resp. en dessous de 0 si cela se produit), tous les résultats sont diminués (resp. augmentés) d'autant de fois 1200 que nécessaire pour rester dans l'intervalle [0,1200[.
Une gamme primitive est exploitable si elle répond à quelques exigences raisonnables :
- L'intervalle minimum séparant deux notes consécutives ne doit pas être trop petit, sous peine de démultiplier inutilement le nombre des notes, ni trop grand, sous peine de créer des lacunes au sein de l'octave. La musique occidentale fixe habituellement la limite inférieure au voisinage de 100 cents (un demi-ton) : outre que le pouvoir de résolution de notre oreille y trouve son compte, cette limite est compatible avec le développement d'une polyphonie qui craint par ailleurs les intervalles trop étroits. D'autres musiques davantage homophoniques (par exemple arabisantes) peuvent abaisser cette limite et explorer les quarts de ton (≈ 50 cents). Une gamme primitive acceptable comporte donc au moins 12 notes mais elle peut en comporter davantage.
- Les notes de la gamme primitive ne peuvent en aucun cas être réparties au hasard au sein de l'octave. Même si l'on trouvait une disposition irrégulière qui donne satisfaction à l'oreille, il subsisterait un grave problème lié à l'absence de transposabilité. La figure ci-dessous illustre cette situation : à gauche, une gamme présumée convenable à l'audition et composées de 12 notes, X, Y, Z, ..., distribuées irrégulièrement à partir de la note de base, X (dite tonique) et à droite, une tentative de transposition par un changement de tonique, de X vers Y. On voit que cette transposition échoue du fait qu'elle fait appel à des notes inexistantes au sein de la gamme primitive (La plupart des flèches pointent dans le vide). Ce défaut de transposabilité est inacceptable pour tout musicien qui veut pouvoir translater une partition vers le grave ou l'aigu, sans perdre la reconnaissance mélodique.
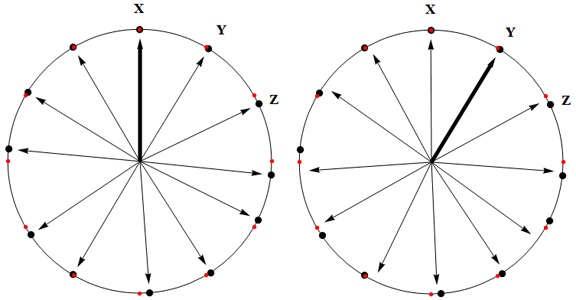
Une condition nécessaire à la transposabilité d'une gamme primitive est que celle-ci soit constituée d'intervalles tous combinaisons linéaires d'un petit nombre d'intervalles élémentaires. C'est trivialement le cas si les notes de la gamme primitive sont équidistantes mais l'exemple ci-après de la gamme pythagoricienne montre cela reste possible même si elles ne le sont pas. En toute rigueur, cette condition est mathématiquement incompatible avec l'exigence assez naturelle de consonance entre les notes, à savoir que leurs rapports fréquentiels se réduisent à des fractions simples. Par bonheur, une compatibilité approchée peut être trouvée qui ne heurte pas l'oreille. Les sections suivantes présentent les gammes primitives en vigueur aux époques médiévale, renaissante, enfin moderne. Elles précisent la nature et l'utilité des modes dans chaque cas.
Les Modes anciens
On qualifie d'anciens (mais pas forcément antiques, cf infra) un ensemble de 7 modes partitionnant la gamme de Pythagore, définie comme suit.
La gamme pythagoricienne

On attribue à l'école de Pythagore (6ème siècle avant notre ère) la construction de la première gamme primitive exploitable. Serrant au plus près l'arithmétique élémentaire, elle y a gagné une pertinence telle qu'elle demeure enseignée de nos jours.
Pythagore et (plus probablement) ses disciples ont assez naturellement choisi de privilégier l'intervalle de quinte (rapport 3/2), le plus consonant de tous après l'octave (rapport 2/1). Ces rapports concernent les sons émis par une corde à vide ou raccourcie de moitié (donnant l'octave supérieure) ou aux deux tiers (donnant la quinte supérieure). On sait aujourd'hui que ces rapports de longueurs de corde correspondent aussi et surtout au rapport (inverse) des fréquences des sons émis.

La gamme pythagoricienne est construite sur la base d'un empilement de quintes : au départ d'une note, fa en l'occurrence afin de respecter la nomenclature en usage, on définit, dans un premier temps, 6 nouvelles notes situées récursivement une quinte plus haut. En multipliant la fréquence d'une note par 3/2, on obtient donc la fréquence de la note suivante à condition de diviser éventuellement le résultat par 2 si l'on est sorti de l'octave considérée. Les 7 notes ainsi définies, nommées, fa, do, sol, ré, la, mi, si, dans l'ordre dit des quintes, constituent la gamme heptatonique de Pythagore. Leurs fréquences sont données par la formule, fm = f0 3m/2Floor[m ℓg3] (m = -1, 0, ..., 4, 5, où Floor[x] désigne la partie entière de x soit le plus grand entier inférieur ou égal à x). On trouve, dans le détail, fk = f0 {1/1 (=fa), 3/2 (=do), 9/8 (=sol), 27/16 (=ré), 81/64 (=la), 243/128 (=mi), 729/512 (=si)}, où la valeur exacte de f0 dépend du diapason choisi. Sur le cercle des quintes, chaque note se positionne à l'abscisse, pyth[m] = 1200 (m ℓg3-Floor[m ℓg3]) cents soit, dans l'ordre des intervalles croissants : 0 (=do), 203.91 (=ré), 407.82 (=mi), 498.045 (=fa), 701.955 (=sol), 905.865 (=la), 1109.78 (=si) et (1200 = do suivant). On observe que tous ces intervalles sont proches d'un multiple de 100 cents, une coïncidence remarquable qui favorisera bien plus tard l'avènement de la gamme tempérée.
La construction pythagoricienne peut être prolongée par empilement de quintes supplémentaires (Cf G&T) : 1) 7 quintes ascendantes au-delà du si (générant la gamme des dièses) et 2) 7 quintes descendantes, en-deçà du fa (générant la gamme des bémols). On obtient la suite,

Ces 21 notes constituant la gamme, pyth21, apparaissent, sur le cercle d'octave, dans l'ordre des fréquences croissantes, fm = f0 3m/2Floor[m ℓg3], aux abscisses, pyth[m] = 1200 (m ℓg3-Floor[m ℓg3]) cents (m = -8, -7, ..., 11, 12).
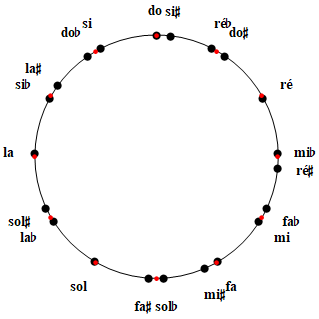
La gamme de Pythagore (à 21 notes) est aisément transposable car tous ses intervalles sont des combinaisons linéaires de deux intervalles élémentaires seulement : le demi-ton diatonique, td = 1200 ℓg(28/35) = 90.225 cents (Ex. les intervalles mi-fa, si-do, ...) et le demi-ton chromatique, tc = 1200 ℓg(37/211) = 113.68 cents, séparant une note de sa variante altérée (Ex. fab-fa, fa-fa#, ...). Le ton, T = 1200 ℓg(9/8) = 203.91 cents, vaut la somme des précédents, T = tc+td (= P + 2td, une variante utile au paragraphe suivant) et le petit comma pythagoricien séparant les notes voisines (dites anharmoniques, ex. réb-do#), vaut : P = tc - td = 1200 ℓg(312/219) = 23.46 cents.
Le mode ionien
Si l'on observe la position des 21 notes pythagoriciennes sur le cercle d'octave, on constate que les intervalles entre les notes consécutives sont de trois types, P, td-P et td, et qu'ils se succèdent dans l'ordre, {P, td-P, P, td, td, P, td-P, P, td, P, td-P, P, td, td, P, td, td, P, td-P, P, td}. C'est la partition la plus serrée de l'octave que le cycle de 20 quintes propose. En soi, elle constitue un mode possible mais musicalement impraticable car faisant intervenir l'intervalle, P, beaucoup trop étroit (23.46 cents) pour être consonant. On trouve assez miraculeusement une bien meilleure partition de l'octave en regroupant les 21 intervalles précédents en 7 sous-listes :
{ {P, td-P, P, td} , {td, P, td-P, P} , {td} , {P, td-P, P, td} , {td, P, td}, {td, P, td-P, P}, {td} } = {T, T, td, T, T, T, td}
Cet arrangement définit le mode heptatonique ionien, encore appelé mode de do. Il est assurément le plus connu parmi tous les modes existants puisqu'il coïncide avec notre mode majeur. On vérifie aisément qu'il partitionne l'octave vu que l'on a bien : 5T+2td = 1200 cents. La figure dynamique suivante affiche le cycle des quintes en mettant en évidence les intervalles du mode ionien grâce à un système de flèche dont l'une, en gras, pointe vers la tonique de départ :
Les 7 flèches pointent vers les autres notes de la gamme secondaire ainsi définie, do-ré-mi-fa-sol-la-si(-do). On la nomme assez naturellement gamme de do en mode ionien ou plus sûrement gamme de do en mode de do (Cf infra).
Rien n'oblige à choisir la note do comme tonique, celle-ci peut être l'une quelconque des 21 notes du cycle. Pour voir comment la gamme est altérée dans ce cas, il suffit de déplacer le curseur situé en bas de la figure précédente : la tonique change ainsi que les autres notes mais bien entendu les intervalles du mode ionien, {T, T, td, T, T, T, td}, sont préservés. Si, par exemple, on choisit ré comme nouvelle tonique, on trouve la gamme de ré en mode de do (ionien) où apparaissent deux altérations en dièse : ré-mi-fa#-sol-la-si-do#(-ré). Vérifiez qu'en mode ionien, seules les 15 toniques appartenant à l'intervalle [dob-do#] (dans l'ordre des quintes) proposent un schéma de notes ne dépassant pas l'altération simple. La gamme de do# en mode de do impose que toutes les notes soient diésées mais si l'on pousse un rang plus loin dans l'ordre des quintes (gamme de sol# en mode de do), on voit qu'une flèche pointe dans le vide, en fait vers un fa double dièse (fa##), qui apparaîtrait si on poursuivait l'empilement des quintes au-delà de 20 (Cf G&T). De même, du côté des bémols, la gamme de dob exige 7 bémols et la gamme précédente, celle de fab, fait appel à un si double bémol (sibb).
Les autres modes anciens
Six autres modes ont été définis qui sont venus s'ajouter au mode ionien. Leur schéma d'intervalles dérive du schéma ionien par simple permutation circulaire. Le tableau suivant les résume (NB : la notation chiffrée des intervalles est commode à condition de se rappeler que le demi-ton diatonique ne vaut pas exactement la moitié d'un ton; cela ne sera vrai qu'en tempérament égal) :

Le mode locrien, longtemps considéré comme dissonant à cause de sa quinte diminuée, n'a jamais fait partie des modes anciens mais on l'a inclus dans le tableau par souci de complétude. On vérifie, en effet, que la Quinte (somme des 4 premiers intervalles) est juste (3T+td = 701.955 cents) pour tous les modes sauf pour le mode locrien où elle est diminuée d'un demi-ton chromatique (2T+2td = 588.27 cents).
Une vidéo dynamique est naturellement possible pour chacun des 6 modes ajoutés et elle permet de visualiser les gammes dans chaque mode :
On peut trouver la liste des notes constitutives de n'importe quelle gamme dans un mode donné par une procédure différente, qui présente l'avantage de mettre en lumière la progression des altérations d'une gamme à l'autre. On commence par afficher la suite de, disons, 26 quintes au départ de sibb, ce qui livre 27 notes, de sibb à la## :
La fenêtre soulignée affiche (dans l'ordre des quintes) les notes constitutives de la gamme de do en mode de do. On trouve les notes constitutives de la gamme de X en mode de Y en déplaçant cette fenêtre comme suit. On commence par compter le nombre, noté Δ, d'intervalles séparant X de Y (positivement si X est situé à droite de Y et négativement sinon). Ensuite, on déplace la fenêtre de Δ notes vers la droite, si Δ est positif, et vers la gauche, si Δ est négatif. Il ne reste plus qu'à réordonner les notes soulignées dans l'ordre naturel des fréquences croissantes au départ de la tonique, X. Si la fenêtre déborde de la suite affichée ci-dessus c'est qu'il convient de la prolonger, à gauche dans l'ordre des bémols et à droite dans celui des dièses. On ne va pas au-delà de Δ=±13 car on serait confronté à l'apparition d'altérations triples dont la musique ne fait aucun usage. Voici deux exemples pour fixer les idées :
- Exemple 1 : gamme de la en mode de sol (mixolydien). Δ = +2 donc déplacer la fenêtre de deux cases vers la droite (sol ré la mi si fa# do#), soit, en commençant par la tonique, la, et en poursuivant dans l'ordre ascendant, la gamme : la, si, do#, ré, mi, fa#, sol. Un raccourci mental est possible si l'on connaît l'ordre d'apparition des dièses dans le cycle des quintes : Δ = +2 implique deux dièses, nécessairement fa# et do# et on complète la gamme par les notes naturelles manquantes, en commençant par la tonique.
- Exemple 2 : gamme de mib en mode de do (ionien). Δ = -3 donc déplacer la fenêtre de trois cases vers la gauche (lab mib sib fa do sol ré), soit en commençant par la tonique, mib, et en poursuivant dans l'ordre ascendant, la gamme : mib, fa, sol, lab, sib, do, ré. Le même calcul mental est également possible : Δ = -3 implique trois bémols, nécessairement sib, mib et lab et on complète la gamme par les notes naturelles manquantes en commençant par la tonique.
Les modes anciens souffrent de redondance, ne serait-ce que parce qu'ils dérivent les uns des autres par simple permutation circulaire de leurs intervalles constitutifs. Le tableau en annexe affiche les 105 gammes dépourvues d'altération multiple, gammes de X (15 possibilités) en mode de Y (7 possibilités). Les toniques, X (en tête de gammes), y sont rangées horizontalement dans l'ordre des quintes ascendantes et les modes, Y, le sont verticalement. On constate que toutes les gammes situées sur une même colonne sont composées des mêmes notes (altérations comprises), seulement permutées circulairement.
Sans doute souhaitez-vous entendre comment sonnent ces modes anciens mais ce n'est pas si simple car aucun instrument moderne à sons fixes n'est prévu pour jouer la gamme pythagoricienne. Il est cependant possible de se faire une bonne idée en les adaptant au piano. Il suffit de remplacer les intervalles pythagoriciens, T (203.91 cents) et td (90.225 cents), par leurs équivalents tempérés, T (200 cents) et t (100 cents), ce qui ne fait guère de différence pour une oreille pas trop exigeante. Chaque mode ancien correspond alors au jeu des seules touches blanches au départ de sa note caractéristique (do pour ionien, ré pour dorien, etc), jusqu'à atteindre l'octave. C'est évidemment pour cette raison qu'on a renommé les modes anciens, mode de do, de ré, etc. La gamme entendue est dans chaque cas la gamme de X en mode de X. Si l'on veut entendre, au piano, la gamme de Y en mode de X, c'est évidemment possible, il suffit de partir de la touche correspondant à la note Y et de progresser en respectant les intervalles du mode, ce qui contraint à passer par un nombre variable de touches noires. En fait, tous les modes anciens étant constitués de 5 tons et 2 demi-tons, la seule chose qui les distingue est la position des demi-tons. C'est elle qui confère son caractère particulier à chacun (Cf ci-après, la section consacrée à la sonorité des modes anciens).
Leonard Bernstein a consacré une leçon aux modes anciens (ou plus exactement à leur adaptation à la gamme tempérée) dans le cadre de ses "Young People's Concerts". Voici quelques extraits significatifs sous-titrés en français, relatifs aux modes dorien (Sibelius, début de la Symphonie n°6, en 4:20), phrygien (Liszt, Rhapsodie hongroise n°2, en 0:57, Rimsky-Korsakov, Scheherazade, en 1:25 et même Brahms, mouvement lent de la Symphonie n°4, en 1:54), mixolydien (Debussy, La Cathédrale engloutie, en 3:25) et lydien (Prokofiev, Lieutenant Kijé, en 1:50, et Sibelius, Symphonie n°4, en 2:50).
La dérive hellénistique
L'appellation "modes anciens" doit être considérée avec circonspection. Il est prudent de distinguer les modes antiques, dont on sait fort peu de choses, et les modes anciens, diversement qualifiés, selon les auteurs et les époques, de médiévaux, grégoriens ou ecclésiastiques. Bien que leurs appellations soient clairement d'origine grecque, les modes anciens décrits ci-avant n'ont jamais été définis tels quels par les grecs et encore moins pratiqués. Les historiens qui ont étudié la question n'ont à leur disposition que des informations de seconde main, datant du Moyen-Age et qui mélangent sans avertissement les acquis antiques à d'autres nettement postérieurs. Comme pour se justifier, on prétend trouver une évocation des modes antiques chez Platon mais on trouve de tout chez ce grand philosophe y compris des passages sur l'Atlantide ..., aussi convient-il de rester prudent. Dans un ouvrage de référence, intitulé fort à propos "L'imbroglio des modes", le musicologue français, Jacques Chailley, confesse d'ailleurs avoir abusé d'aspirine en tentant de s'y retrouver.
Rapportons simplement que les grecs n'ont explicitement défini que les modes dorien, phrygien, lydien et mixolydien, dans une forme qu'ils ont qualifiée d'authent(iqu)e. Il est impensable qu'ils n'aient pas remarqué que la suite des intervalles de chacun se suivait au travers d'une simple permutation circulaire des intervalles (Vérifiez en comparant les lignes 2 à 5 du tableau des modes anciens). Ils avaient donc tous les éléments en main pour poursuivre la manoeuvre circulaire et définir les 3 modes restants. Au lieu de cela, ils se sont égarés en inventant pour chacun une variante, dite plagale, obtenue en permutant le tétracorde final de la forme authente (ses 3 derniers intervalles) et le tétracorde initial (les 3 premiers intervalles) :
N1 N2 N3 N4 N5 N6 N7 (f. authente : dorien, phrygien, lydien ou mixolydien)
N5 N6 N7 N1 N2 N3 N4 (f. plagale : hypodorien, hypophrygien, hypolydien ou hypomixolydien)
Dans tous les cas, la note N5 est située une quinte au-dessus de N1 ou une quarte en-dessous, ce qui revient au même (D'où le préfixe "hypo"). En jouant avec les applications dynamiques ci-dessus, vous pouvez vérifier que la gamme de ré en mode lydien soit, (ré-mi-fa#)-sol#-(la-si-do#), devient (la-si-do#)-ré-(mi-fa#-sol#), en mode hypolydien, qui n'est rien d'autre que la gamme de la en mode ionien.
Par ce procédé, l'hypolydien donne naissance à l'ionien, l'hypodorien à l'éolien, l'hypophrygien au locrien, et le mixolydien retourne au dorien. Au bilan, les grecs se sont retrouvés avec 8 modes quand 7 auraient suffi, le mode hypomixolydien faisant double emploi avec le mode dorien déjà présent en forme authente. Pourquoi faire simple quand on peut faire compliqué ? Euclide (4ème siècle avant J-C) s'était montré mieux inspiré dans ses rigoureux Eléments de Géométrie.
Note. Ces subtilités (qui n'en sont pas vraiment) ont jeté le trouble parmi les auteurs, au 19ème siècle, au point qu'ils ont erronément renommés les 7 modes anciens (do = lydien, ré = phrygien, mi = dorien, fa = hypolydien, sol = hypophrygien, la = hypodorien et si = mixolydien). C'est pour éviter toute confusion que l'on préfère actuellement s'en tenir aux appellations modernes, modes de do, de ré, etc. Les modes éolien et ionien ainsi que leur variante plagale (hypoéolien et hypoionien) n'ont été ajoutés qu'au Moyen-Age, faisant passer bien inutilement le total des modes à 12, d'où le titre du fameux traité d'Heinrich Glaréan (Dodecachordon, 1567). Le mode locrien, peu pratiqué du fait de sa quinte diminuée peu flatteuse pour l'oreille, est encore plus tardif.
L'élégance de la gamme pythagoricienne a sans doute entretenu, chez les grecs, l'espoir d'une théorie mathématique de la musique. Aussi limpide qu'imparable, à ses débuts, elle a ouvert la voie à une définition claire des 7 modes anciens mais, inexplicablement, les théoriciens de l'époque se sont égarés dans des digressions compliquées qui les ont éloignés d'une pratique musicale exploitable : dès lors, la musique grecque est demeurée homophonique pour un résultat médiocre, sans aucun rapport avec celui atteint dans les arts de la représentation (sculpture et architecture) au siècle de Péricles (-495, -429). On pourrait tenter une explication au motif que l'instrumentarium demeurait limité pour des raisons techniques évidentes mais cela ne justifie rien car même le chant n'a connu aucun développement digne de ce nom. La musique savante, née dans le Nord de la France au Moyen-Age, ne disposait pas non plus d'instruments sophistiqués mais un chant polyphonique est né dans l'attente, qui a permis l'éclosion d'un art déjà sans pareil. C'est à ce point que parler de Renaissance en musique, à partir de 1500, apparaît comme un contresens manifeste, aucun modèle antique n'ayant guidé l'exploration d'un art qui a dû s'inventer pratiquement de toutes pièces.
La gamme zarlinienne


On rapporte que le modèle pythagoricien aurait été contesté dès l'Antiquité par Aristoxène (-360, -300), à qui l'on prête la recommandation de juger la valeur des consonances en se fiant autant au jugement auditif qu'aux proportions simples. Sous réserve que cette information soit exacte, on y voit une première tentative de mettre en doute la nécessité de n'obéir qu'à une logique arithmétique et d'assurer un avenir à l'intuition musicale. On crédite habituellement Gioseffo Zarlino (1517-1590) et Johannes Lippius (1585-1612) d'avoir relayé cette idée en la formalisant.
Le (plain) chant grégorien, essentiellement horizontal, a eu largement recours aux modes anciens. S'il convenait aux sobres monastères, il n'était plus vraiment en accord avec la verticalité des cathédrales alors en pleine érection. La polyphonie verticale allait montrer une nouvelle voie, encore fallait-il dégager les règles de compatibilité dans la superposition des notes.
Au Moyen-Age, les musiciens occidentaux ont continué de privilégier la quinte (rapport 3/2, juste par construction, donc aussi la quarte, rapport 4/3, son complément naturel au sein de l'octave, 701.955+498.045=1200 cents). Ils ont délaissé la tierce pythagoricienne (81/64, soit 407.82 cents) au motif qu'elle ne coïncidait pas avec la tierce majeure acoustiquement pure (rapport 5/4, soit 386.314 cents). Ce faisant, ils l'ont reléguée au rang des dissonances infréquentables. Seuls les anglais ont cultivé cette tierce légèrement fausse, trouvant un plaisir auditif dans les frottements qu'elle engendrait. Mais avec le temps et le commerce des épices, l'idée a fait son chemin parmi les musiciens continentaux qu'il serait temps d'apprivoiser cette tierce et de la (ré)concilier avec la quinte et naturellement l'octave.
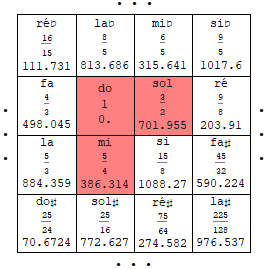
Quintes ascendantes de gauche à droite
Tierces ascendantes de haut en bas
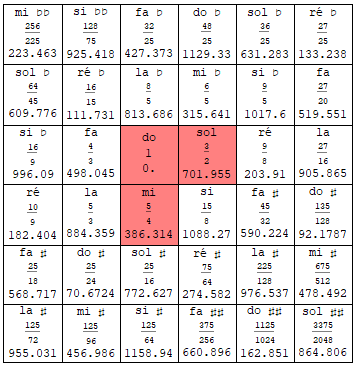
Zarlino a tenté une généralisation de la gamme pythagoricienne par empilement de quintes et de tierces pures : elle conserve la quinte (rapport 3/2) mais lui adjoint la tierce (majeure, rapport 5/4). On obtient le tableau bidimensionnel ci-dessus à gauche, où la progression horizontale, de gauche à droite, correspond aux quintes ascendantes et où la progression verticale, de haut en bas, correspond aux tierces ascendantes. Les notes do-mi-sol (cases peintes en rose) dessinent le dénommé "accord parfait majeur" et il peut être reproduit autant de fois qu'on le souhaite, il suffit de répéter le motif "en coin" au sein du tableau (Par exemple les classiques, fa-la-do et sol-si-ré mais aussi mib-sol-sib, etc, vérifiez vos fractions !). On retrouve les notes usuelles sur base de trois accords parfaits, do-mi-sol (en rose), fa-la-do (à sa gauche) et sol-si-ré (à sa droite).
Les fréquences des 16 premières notes zarliniennes au sein d'une octave unique, [f0(=doi)- 2f0(=doi+1)[, répondent à la loi, fm,n = f0 3m 5n/2Floor[m ℓg3+n ℓg5] (m, n = -1, 0, 1, 2), où la valeur exacte de f0 dépend comme toujours du diapason choisi. Les intervalles entre ces notes et le do de base valent, zarl[m,n] = 1200 (m ℓg3+n ℓg5-Floor[m ℓg3+n ℓg5]), et on les a reportés sur le cercle d'octave ci-dessus.
Cette gamme primitive à 16 notes est en principe transposable car ses intervalles constitutifs (td+P-2Z, 3Z-P, td+P-Z et td+Z) sont des combinaisons linéaires de 3 intervalles élémentaires, td, P et Z (défini ci-après). La figure dynamique suivante affiche la gamme de do en mode zarlinien de do : celui-ci ressemble au mode ionien du fait d'un schéma similaire d'intervalles sauf que les valeurs en cents sont légèrement différentes (Comparez les figures correspondantes pour le vérifier).
Des problèmes de transposabilité existent cependant : si l'on change de tonique, de do vers ré par exemple, trois flèches pointent dans le vide, ce qui indique que la gamme de Zarlino à 16 notes est très loin de suffire à elle-même. On pourrait tenter de remédier à la situation en élargissant le tableau 4x4 précédent en un tableau 6x6, ce qui ferait passer la gamme de 16 à 36 notes, avec l'espoir que les trois notes manquantes figureraient parmi les 20 notes ajoutées. Poursuivons donc l'empilement horizontal des quintes et vertical des tierces, on trouve :
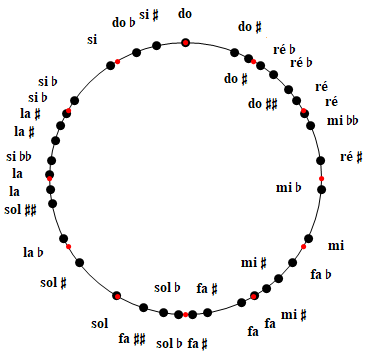
On voit apparaître des variantes de notes qui sont absentes dans la construction pythagoricienne, c'est le prix à payer lorsqu'on tente de concilier les quintes et les tierces. Par exemple, la note située à gauche du la (5/3) est clairement un ré puisque située une quinte plus bas. Toutefois ce ré (rapport 10/9, 1200 ℓg(10/9) = 182.40 cents) est légèrement plus grave (d'un comma zarlinien, Z = 1200 ℓg(81/80) = 21.506 cents) que le ré (9/8, 1200 ℓg(9/8) = 203.91 cents) déjà présent au tableau 4x4 et cette situation a tendance à se reproduire avec d'autres notes.
Dans la conception de Zarlino, les variantes de ré, 9/8 et 10/9 (ou de la, 5/3 et 27/16, etc ... ) sont aussi valables l'une que l'autre; cependant elles posent problème. Non seulement la notation doit pouvoir les distinguer mais les claviers ordinaires à sons fixes ne conviennent plus pour les matérialiser toutes. Plus grave, la démultiplication des notes homonymes croît à mesure qu'on étend le réseau zarlinien, au point qu'on se trouve bien vite confronté à une pléthore difficilement gérable.
On est à présent en mesure de préciser la nature de deux des trois notes manquantes dans la gamme à 16 notes lors de la transposition de do vers ré : ce sont en fait des variantes de la (la 27/16, 905.865 cents) et de do# (do# 135/128, 92.1787 cents). Quant à la troisème note manquante, un mi (81/64, 407.82 cents), il ne fait même pas partie de la gamme à 36 notes, il en faudrait 64 !
En résumé, la gamme zarlinienne est transposable mais elle ne l'est que partiellement : il manque sans cesse des notes lorsqu'on change de tonique et lorsqu'on tente d'élargir la gamme pour pallier le problème, celui-ci se repose intact.
La multiplication des notes zarliniennes entraîne une prolifération des modes du fait que l'octave peut être "pixellisée" de multiples façons : si l'on s'en tient à la gamme à 36 notes, il ne faut pas moins de 7 intervalles élémentaires, td+P-2Z, Z, 2Z-P, td+2P-4Z, td+2P-5Z, 3Z-P et td+P-3Z, pour la décrire, c'est beaucoup trop. Du coup, la notion de mode y a perdu de sa pertinence, elle est même passée au second plan, supplantée par celle du choix d'un bon tempérament. Cette notion essentielle en musique ancienne ayant été détaillée dans G&T, bornons-nous à rappeler que 12 quintes étant trop longues de P = 23.46 (cents) pour refermer exactement l'octave et que 4 quintes étant trop longues de Z = 21.506 (cents) pour fabriquer une tierce majeure pure, il faut, d'une manière ou d'une autre, raccourcir ces quintes (tempérer est le terme exact) donc les fausser légèrement. Concilier octaves, quintes et tierces peut se faire de diverses manières mais toujours approximativement à cause d'une impossibilité arithmétique : on trouve dès lors sur le marché toutes sortes de tempéraments approchés, plus ou moins compatibles avec une transposition dans tous les tons.
Ayant apprivoisé les tierces enfin admises au rang de consonances, la Renaissance (1430-1600) a développé une écriture polyphonique verticale où l'accord parfait (octave-quinte-tierce) a régné sans partage. Obsédée par la pureté des tierces, elle a cultivé un son lisse, sans tension ni résolution (Palestrina, Victoria), qui ne pouvait durer éternellement. Elle a inévitablement fait un pas de côté lorsqu'elle a épuisé le sujet. Un nouveau chapitre de l'histoire musicale s'est alors ouvert, c'est l'ère du Baroque (1600-1750). La gamme zarlinienne est tombée aux oubliettes et la modalité a refait surface dans une forme sérieusement allégée.
L'émergence de la tonalité
Le baroque musical s'est décliné en deux temps, l'un largement vocal, de Monteverdi à Cavalli, et l'autre, postérieur, bénéficiant de l'essor phénoménal de l'instrumentarium, en particulier de la lutherie crémonaise. C'est le baroque tardif qui a appelé une réforme pertinente des modes anciens.
Dérivant les uns des autres par permutations circulaires de leurs intervalles constitutifs, les modes anciens partagent une information commune et on ne devrait rien perdre d'essentiel en n'en gardant qu'un seul. Telle est l'idée à la base de la notion de tonalité :
- Elle conserve intact le mode de do (ionien) dont la déclamation ascendante affirme le caractère conquérant. Renommé mode majeur (M), sa signature intervallique coïncide évidemment avec celle du mode ionien, T-T-td-T-T-T-td.
- Toutefois, un deuxième mode davantage introverti a été jugé nécessaire, pour faire contraste, et il a pris le nom de mode mineur (m, dit harmonique). Il dérive du mode majeur en affectant d'un bémol ses degrés III et VI (les notes modales), ce qui revient à les abaisser d'un demi-ton chromatique. La signature du mode mineur harmonique est donc, T-td-T-T-td-(T+tc)-td, ce qui l'apparente au mode éolien, par la position de ses deux premiers demi-tons. On récapitule comme suit le passage du mode majeur au mode mineur harmonique :
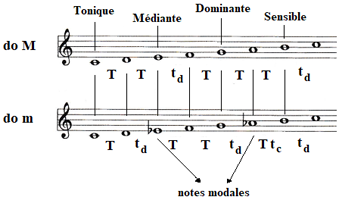
Note. L'intervalle élargi, T + tc , propre au mode mineur harmonique est difficilement chantable. C'est pourquoi on relève éventuellement son 6ème degré d'un demi-ton diatonique ce qui mène au schéma du mode mineur mélodique (ascendant). Dans l'exemple, do m, la gamme mélodique s'énonce donc : do ré mib fa sol la si (do).
Chaque note occupe un degré de la gamme. On n'a mentionné sur la figure que les degrés impairs, les plus significatifs. Dans la gamme majeure, les notes successives sont à une distance de seconde, de tierce (M), de quarte, de quinte, de sixte (M), de 7ème et d'octave par rapport à la tonique de départ.
Chaque degré exerce une fonction tonale au sein de la phrase musicale. La tonique, premier mais aussi 8ème degré de la gamme, est importante car, dans une phrase musicale, elle fonctionne souvent à la manière d'un point final. La sensible n'est pas moins importante du fait de l'attraction qu'elle subit de la part de la tonique lorsqu'elle n'est qu'à une distance d'un demi-ton (Par exemple, décliner la gamme de do M en mouvement conjoint ascendant demande de terminer sur un rappel de la tonique, le do suivant, sous peine de créer un point de suspension appelant une résolution).
La musique instrumentale à partir de 1700 a adopté cette modalité restreinte aux seuls modes majeur et mineur. Par exemple, les 4 Saisons de votre enfance sont clairement référencées dans les tonalités de mi M (Printemps), sol m (Eté), fa M (Automne) et fa m (Hiver).
A l'époque classique, la dichotomie majeur-mineur est devenue la règle et la théorie s'est calée sur ce modèle. En particulier, chaque mode s'est trouvé caractérisé par un ensemble d'altérations systématiques, dièses ou bémols, qui ont pu être mises en évidence à la clé. C'était, de fait, un bel exemple de simplification d'une théorie ancienne inutilement alambiquée. Tonalité et modalité ne s'opposent pas : la première est un cas particulier de la seconde, choisie pour sa pertinence musicale ... jusqu'à ce qu'elle épuise ses effets, doucement à partir de 1850.
Comment sonnent les modes anciens ?
Nous savons comment faire sonner approximativement les modes anciens au piano : pour rappel, on entend la gamme de X en mode de X (X ∈ {do, ré, mi, fa, sol, la, si}) en jouant les touches blanches au départ de la note X jusqu'à la même note située une octave plus haut.
Il est moins facile de reconnaître ces modes anciens dans le feu de l'action musicale tant nos oreilles ont été habituées, pendant trois siècles, aux sonorités des modes majeur et mineur. Et pourtant ils sont moins rares qu'il y paraît, surtout depuis le regain d'intérêt pour les musiques nationales, amorcé vers le milieu du 19ème siècle. Une façon d'aborder le problème consiste à comparer n'importe quelle la gamme de X en mode de X à la gamme de X en mode majeur (ou mineur, c'est à voir selon les cas) et à regarder comment on passe de la première à la seconde.
- Mode Ionien (X=do). Ce cas est simpliste puisque la gamme de do en mode de do (ionien) n'est autre que la gamme de do majeur donc elle sonne comme elle, do-ré-mi-fa-sol-la-si-do. Ce sont les autres cas qui sont intéressants.
- Mode Lydien (X=fa). La gamme de fa M est connue : fa-sol-la-sib-do-ré-mi-fa (Si vous doutez, retournez à l'application dynamique du mode majeur au paragraphe précédent). Si on la compare à la gamme de fa en mode de fa (lydien), on trouve : fa-sol-la-si-do-ré-mi-fa. On constate que le degré IV est augmenté d'un demi-ton chromatique. Cette quarte augmentée signe le mode lydien. Le mouvement lent du Quatuor n°15 de Beethoven est un exemple assez unique dans la musique de cette époque d'une écriture en mode lydien : il accentue l'atmosphère d'intériorité voulue par le compositeur célébrant une guérison attendue.
- Mode Mixolydien (X=sol). La gamme de sol M est connue : sol-la-si-do-ré-mi-fa#-sol. La gamme de sol en mode de sol (mixolydien) s'énonce : sol-la-si-do-ré-mi-fa-sol. On constate, cette fois, que c'est le degré VII qui est diminuée d'un demi-ton chromatique. C'est cette septième diminuée qui signe le mode mixolydien, la soustrayant à l'attraction vers l'octave. La tension qui en résulte a été très pratiquée en jazz mais pas seulement : La Cathédrale engloutie, l'un des Préludes du Premier Livre de Debussy, fait également usage de ce mode.
- Dorien (X=ré). La gamme de ré m est connue : ré-mi-fa-sol-la-sib-do-ré (Si vous doutez, retournez à l'application dynamique du mode mineur au paragraphe précédent). La gamme de ré en mode de ré (dorien) s'énonce : ré-mi-fa-sol-la-si-do-ré. On constate, cette fois, que c'est le degré VI, la sixte, qui est augmentée d'un demi-ton chromatique. La Toccata & Fugue BWV 538 de J-S Bach est de ce type, ré m sans bémol à la clé.
- Mode Eolien (X=la). Ce mode est peu utilisé en musique classique. Par rapport à la gamme de la m (la-si-do-ré-mi-fa-sol#-la), la gamme de la en mode de la (éolien) présente une septième diminuée d'un demi-ton chromatique : la-si-do-ré-mi-fa-sol-la.
- Mode Phrygien (X=mi). La gamme de mi m est connue : mi-fa#-sol-la-si-do-ré#-mi. La gamme de mi en mode de mi (phrygien) s'énonce : mi-fa-sol-la-si-do-ré-mi. Cette fois, deux degrés, II et VII, sont diminués d'un demi-ton chromatique. Ces deux altérations confèrent au mode phrygien un caractère triste, perceptible dès le début de la Rhapsodie hongroise n°2 de Franz Liszt.
- Le cas, X=si, correspondant au mode locrien n'est pas considéré. La gamme de si en mode de si (locrien), si-do-ré-mi-fa-sol-la-si, possède une quinte diminuée dissonante qui rend ce mode inusité.
La modalité généralisée
Avec l'usure du temps, la tonalité a fini par épuiser ses effets. Un relâchement a bien été tenté, consistant à déroger localement aux règles du mode en multipliant les altérations accidentelles. C'est la stratégie adoptée par Liszt et Wagner pour libérer la musique du carcan tonal et ouvrir, à terme, la porte à l'atonalité, on y reviendra. Par ailleurs, l'émergence des écoles nationales a suscité un intérêt croissant pour les musiques populaires dont certaines pratiquaient depuis toujours des modes totalement inusités. Ces deux circonstances ont ouvert la porte à un élargissement de la modalité donc à une diversification des atmosphères musicales. L'adoption du tempérament égal a été l'instrument de cette ouverture.
La gamme chromatique à 12 sons
Vers 1800 sinon en pratique bien avant, la saga des tempéraments divers et variés s'est (définitivement ?) clôturée sur un compromis qui a contrarié les puristes mais qui a réjoui tous ceux qui pensaient avec pragmatisme qu'il était temps d'opter pour le tempérament égal grâce auquel le problème de la transposition trouvait enfin une solution imparable.
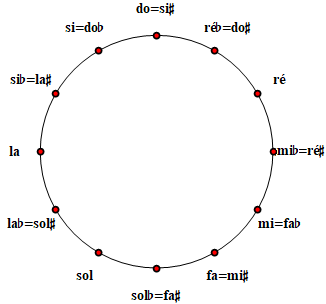
Tout est parti de cette observation que les notes pythagoriciennes voire zarliniennes ont nettement tendance à se grouper aux voisinages des sommets d'un dodécagone régulier (Les points rouges sur toutes les figures qui précèdent). Les musiciens ont dès lors pris la décision radicale de confondre ces paquets de notes dites anharmoniques en une note unique, tout en se réservant la possibilité de les noter différemment selon leur fonction tonale. C'est le principe d'une orthographe musicale où des notes sonnant à l'identique peuvent s'écrire différemment en fonction du sens que l'on veut donner à la phrase.
La gamme tempérée est une invention ancienne qui ne s'est véritablement imposée qu'à partir des années 1800, le temps nécessaire pour vaincre les réticences. Les fréquences des 12 notes (dites chromatiques) appartenant à une octave unique répondent à la loi, fm = f0 2m/12 (Hz, m = 0, 1, ..., 11), où la valeur de f0 dépend du diapason adopté. Sur le cercle d'octave, les notes occupent les points rouges aux abscisses, temp[m] = 100 m; elles sont espacées de 100 cents, valeur exacte du demi-ton tempéré, t, qui remplace td et tc. L'échelle complète des fréquences audibles, couvrant 10 octaves, est représentée au tableau suivant avec un diapason fixé à la valeur de la440 Hz.
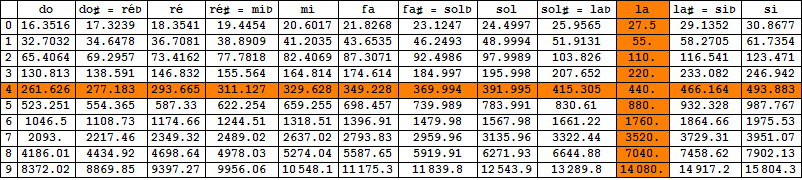
La gamme (chromatique) tempérée peut servir de gamme primitive pour un inventaire complet des modes modernes. Elle s'énonce : do-do#(=réb)-ré-ré#(=mib)-mi-fa-fa#(=solb)-sol-sol#(=lab)-la-la#(=sib)-si. Si elle n'est sans doute pas idéale en ce qui concerne la justesse de ses intervalles, cela est plus que largement compensé par le fait qu'elle est totalement transposable puisque ses intervalles constitutifs se réduisent au seul demi-ton, t. Pour transposer dans n'importe quelle tonalité, il suffit donc de décaler toutes les notes du multiple approprié de 100 cents.
Les modes de la gamme chromatique à 12 sons
La gamme chromatique semble le compromis idéal entre justesse et transposition. Cependant la décliner en montant (ou en descendant) répand un sentiment de monotonie qui frise l'ennui (Jouez toutes les touches blanches et noires sur ce piano virtuel). Au vu de ce qui vient d'être dit, le remède est connu, il consiste à s'en tenir à quelques modes bien choisis. Grâce à l'égalité de ses intervalles constitutifs, la gamme chromatique permet l'inventaire exhaustif de tous les modes possibles.
Rappelons que le principe de la modalité est de se concentrer sur un sous-ensemble d'intervalles couvrant l'octave de référence. Par exemple, le mode majeur, construit sur la suite d'intervalles T-T-t-T-T-T-t, soit, 200-200-100-200-200-200-100 si l'on travaille en cents. En divisant ces intervalles par 100 on obtient une notation condensée valable pour le mode majeur soit {2, 2, 1, 2, 2, 2, 1} dont le total vaut 12 comme il se doit. On entend le mode majeur si on presse les seules touches blanches du piano virtuel, au départ du do. Si on presse les seules touches noires, on définit un mode pentatonique répondant au schéma, T-Tt-T-T-Tt = {2, 3, 2, 2, 3}, et on vérifie, à nouveau, que le total fait 12. Ce mode, répandu en Extrême-Orient, peut évidemment être joué au départ de n'importe quelle tonique, à condition de respecter la suite des intervalles.
On fait l'inventaire complet des modes en cherchant toutes les compositions arithmétiques de l'entier 12, définies comme étant les sommes ordonnées d'entiers positifs livrant un total égal à 12. Par exemple, le mode majeur correspond à la composition, 12 = 2+2+1+2+2+2+1 et le mode pentatonique considéré ci-avant correspond à la composition, 12 = 2+3+2+2+3 (Mais il en existe quatre autres, obtenus par permutation circulaire des intervalles : 12 = 3+2+2+3+2 = 2+2+3+2+3 = 2+3+2+3+2 = 3+2+3+2+2).
On démontre, en arithmétique, que tout entier, N, admet 2N-1 compositions distinctes. Par exemple, l'entier N=4 admet 23=8 compositions, à savoir : 4, 1+3, 2+2, 3+1, 1+1+2, 1+2+1, 2+1+1 et 1+1+1+1. Dans le cas qui nous intéresse, N=12, il existe donc 211=2048 modes différents. Dans le détail, ils se répartissent en nk = C11k modes comprenant k intervalles (k=1, 2, ..., 12), soit la suite de valeurs, nk = {1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1}, la 12ème ligne du triangle de Pascal pour les matheux. On vérifie que le total vaut bien 2048.
Il est possible de numéroter ces 2048 modes d'une infinité de manières mais l'une d'elle semble naturelle, qui range les modes dans l'ordre croissant du nombre d'intervalles constitutifs et, à nombre égal, en suivant l'ordre lexiconumérique. Avec cette convention :
- Le mode n°1 répond à la composition {12} soit un intervalle de 1200 cents couvrant l'octave à lui seul; la gamme correspondante ne comporte qu'une seule note et l'échelle sonore complète n'est faite que des do successifs, une formule pas très intéressante !
- Les 11 modes suivants (n°2 à 12) ne comportent que 2 intervalles soit, dans l'ordre lexiconumérique, {1,11} (gamme do-do#-do), {2, 10} (gamme do-ré-do), {3, 9} (do-ré#-do), etc jusqu'à {11,1} (gamme do-si-do). Ces 11 gammes à deux notes sont également inintéressantes.
- On passe ensuite tout aussi rapidement sur les 55 compositions à 3 intervalles, {1, 1, 10}, {1, 2, 9}, {1, 3, 8}, {1, 4, 7}, ..., et sur les 165 compositions à 4 intervalles, {1, 1, 1, 9}, {1, 1, 2, 8}, {1, 1, 3, 7}, ..., car elles définissent des gammes à moins de 5 notes, exagérément lacunaires.
- Poursuivant de la même manière, il existe 330 modes pentatoniques numérotés de 233 (1+1+1+1+8) à 562 (8+1+1+1+1). Les extrêmes sont peu intéressants car ils répartissent les notes fort inégalement au sein de l'octave. Par contre le mode pentatonique, 2+3+2+2+3, considéré ci-avant, porte le n°408. Avec ses variantes circulaires, il est utlisé en Chine ... ou en Occident, lorsqu'on veut évoquer ce lointain pays parfois jusqu'à la caricature. On trouve un exemple dans l'oeuvre célèbre de Maurice Ravel, Ma Mère l'Oye, Laideronnette Impératrice des Pagodes, en 7:50.
- Parmi les 462 modes à 6 intervalles, il en est un qui a fait fortune, c'est le mode n°849, dit "par tons". Répondant à la composition, 2+2+2+2+2+2, il a effectivement été utilisé par Claude Debussy, par exemple dans Voiles, extrait du 1er Livre des Préludes. Ce mode est particulier car il n'est transposable que d'une seule manière, par translation d'un demi-ton; toute autre transposition restituerait en effet les mêmes notes. C'est le premier mode à transposition limitée à avoir été vulgarisé.
- Parmi les 462 modes heptatoniques, on retrouve évidemment les modes majeur (n°1361) et mineur (n°1324) tempérés ainsi que leurs variantes héritées des modes anciens par permutations circulaires.
Les modes à transpositions limitées
L'immense majorité des modes chromatiques, soit 2010 sur 2048 (dont les modes majeur et mineur), autorisent les 12 transpositions possibles sur les degrés de la gamme chromatique, livrant à chaque fois une gamme différente. A contrario, 38 modes ne permettent qu'un nombre restreint de transpositions. Ce sont les modes dont la formule présente un motif combinatoire répétitif. Tel est le cas du mode n°849 (par tons), de formule 2+2+2+2+2+2, qui répète (six fois) la cellule 2 mais aussi du mode n°1594, de formule 1+1+3+1+1+1+3+1, qui répète (deux fois) la cellule 1+1+3+1. Le premier n'autorise que 2 transpositions tandis que le deuxième n'en autorise que 6. La règle est que le nombre de transpositions autorisées vaut le quotient de 12 par le nombre de motifs élémentaires répétés. La division est assurée de tomber juste car la périodicité du motif est toujours un diviseur de 12.
On crédite habituellement Olivier Messiaen (1908-1992) d'avoir isolé 7 modes à transpositions limitées, d'en avoir étudié les propriétés harmoniques et de les avoir pratiqués. Ces modes répertoriés de I à VII possèdent les caractéristiques suivantes :
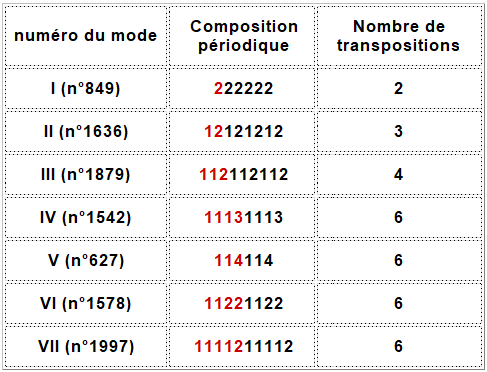
Remarque. En jouant avec l'application dynamique relative au mode V (114114, simple exemple), vous pouvez vérifier que la gamme de fa s'énonce, fa-fa#-sol-si-do-do#, et qu'elle ne diffère pas fondamentalement de la gamme de do en mode V permuté circulairement (141141) soit, do-do#-fa-fa#-sol-si-do. Cette remarque qui vaut pour tous les modes tempérés dispense de détailler les classes d'équivalence obtenues par permutation circulaire des intervalles.
Bien qu'une analyse détaillée dépasse le cadre de cet exposé élémentaire, indiquons quelques exemples musicaux ayant recours à ces modes particuliers. Le mode I n'a pas été inventé par Messiaen ni d'ailleurs par Debussy : il a été utilisé par plusieurs compositeurs avant lui, en particulier par l'école russe et par Gabriel Fauré dans son Impromptu n°5. On trouve le mode II (octotonique) chez Bela Bartok (Suite opus 14, en 4:16) ou dans le Tambourin, 3ème Danse symphonique de Maurice Duruflé. Quant à Messiaen, il a mis sa théorie en pratique dans l'une de ses oeuvres pour orgue les plus connues, La Nativité du Seigneur.
Messiaen croyait son inventaire complet mais il ne l'était pas : il manquait les modes n°712 (1+3+1+3+1+3), 684 (1+2+3+1+2+3) et 720 (1+3+2+1+3+2) (On ne compte plus les permutations circulaires, cf la remarque précédente). Il manquait également les modes, n°7 (6+6), 43 (4+4+4), 98 (1+5+1+5), 135 (2+4+2+4), 164 (3+3+3+3), 186 (4+2+4+2) et 202 (5+1+5+1), mais ce n'était certainement pas un oubli car ces modes comportant moins de 5 intervalles sont inexploitables. Enfin, il y a lieu de réserver un traitement à part au mode entièrement chromatique, n°2048 (1+1+1+1+1+1+1+1+1+1+1+1).
Le mode 2048 : l'atonalité dodécaphonique
Le dernier mode (n° 2048) est particulier puisqu'il inclut la totalité des notes de la gamme primitive. Il n'est pas transposable car toute tentative en ce sens mènerait à une gamme identique à celle de départ. Il génère une gamme, dite dodécaphonique, où les 12 sons sont traités à égalité, c'est-à-dire sans la moindre hiérarchie entre ses degrés, dépourvus en particulier d'un centre tonal.
Le courant atonal a été initié par Arnold Schoenberg (1874-1951), vers 1910, et il s'est propagé, avec plus ou moins de bonheur, à la classe de ses élèves (Alban Berg (1885-1935), Suite Lulu, arrangée à partir d'éléments de son opéra éponyme, à la demande du grand chef Erich Kleiber) et plus généralement chez ses adeptes, un peu partout dans le monde.
Ce courant musical n'a guère été apprécié du grand public et le passage encore plus radical à l'étape sérielle n'a pas arrangé les choses. Un grand nombre de compositeurs d'après-guerre (40-45), comprenant que la voie était probablement sans issue, sont alors revenus non pas forcément à la néo tonalité, ce qui aurait constitué une régression, mais plutôt à une modalité généralisée. C'est la nouvelle vogue du courant postmoderne, réceptacle de toutes les traditions passées, présentes et à venir.