Simple binary Turing machines, their numbering, behaviour and output.
1. Wolfram’s numbering scheme of Turing machines with s states and k characters, half infinite tape and no explicit halting state.
Number of Turing machines with s states and k characters (binary machines are enligthed) :
![]()
| s→2 | s→3 | s→4 | s→5 | |
| k→2 | 4096 | 2985984 | 4294967296 | 10240000000000 |
| k→3 | 2985984 | 198359290368 | 36520347436056576 | 14348907000000000000000 |
| k→4 | 4294967296 | 36520347436056576 | 1208925819614629174706176 | 109951162777600000000000000000000 |
| k→5 | 10240000000000 | 14348907000000000000000 | 109951162777600000000000000000000 | 2980232238769531250000000000000000000000000 |
Instructions table of a machine whose rule number is given (instructions refers to Wolfram’s original mode but shiftedinstructions should have been more judicious) :
![]()
![]()
![]()
![]()
![]()
![]()
Rule number of a machine whose instructions table is given :
![]()
![]()
![]()
Clearly TMNumber annihilates instructions :
![]()
![]()
The s×k triplets, (s,k,d), associated to a given rule, in Wolfram’s canonical order (s =1, 2, ...; k=0, 1, ...; d=-1,+1) :
![]()
![]()
![]()
The same triplets in shifted mode (s =0, 1, ...; k=0, 1, ...; d=0,1) :
![]()
![]()
![]()
Recovering the machine rule number from the shifted triplets :
![]()
![]()
![]()
![]()
Analysis of the 4096 2-states binary machines.
Activation of preliminary instructions :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Search for the first time a new sequence is printed :

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
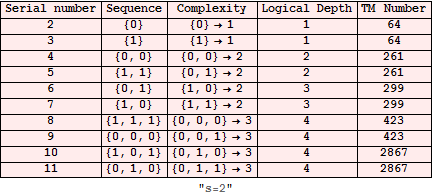
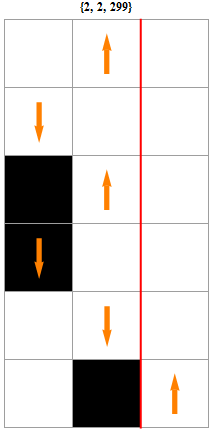
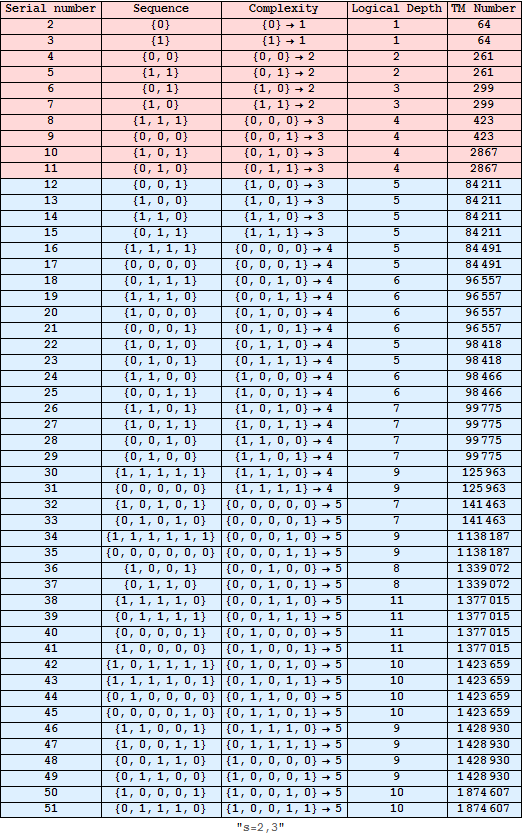
Summary when s=2 (Symmetric sequences have been set as equals) :
![]()
![]()

![]()
![]()
Analysis of the 2985984 3-states binary machines.
Activation of preliminary instructions :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
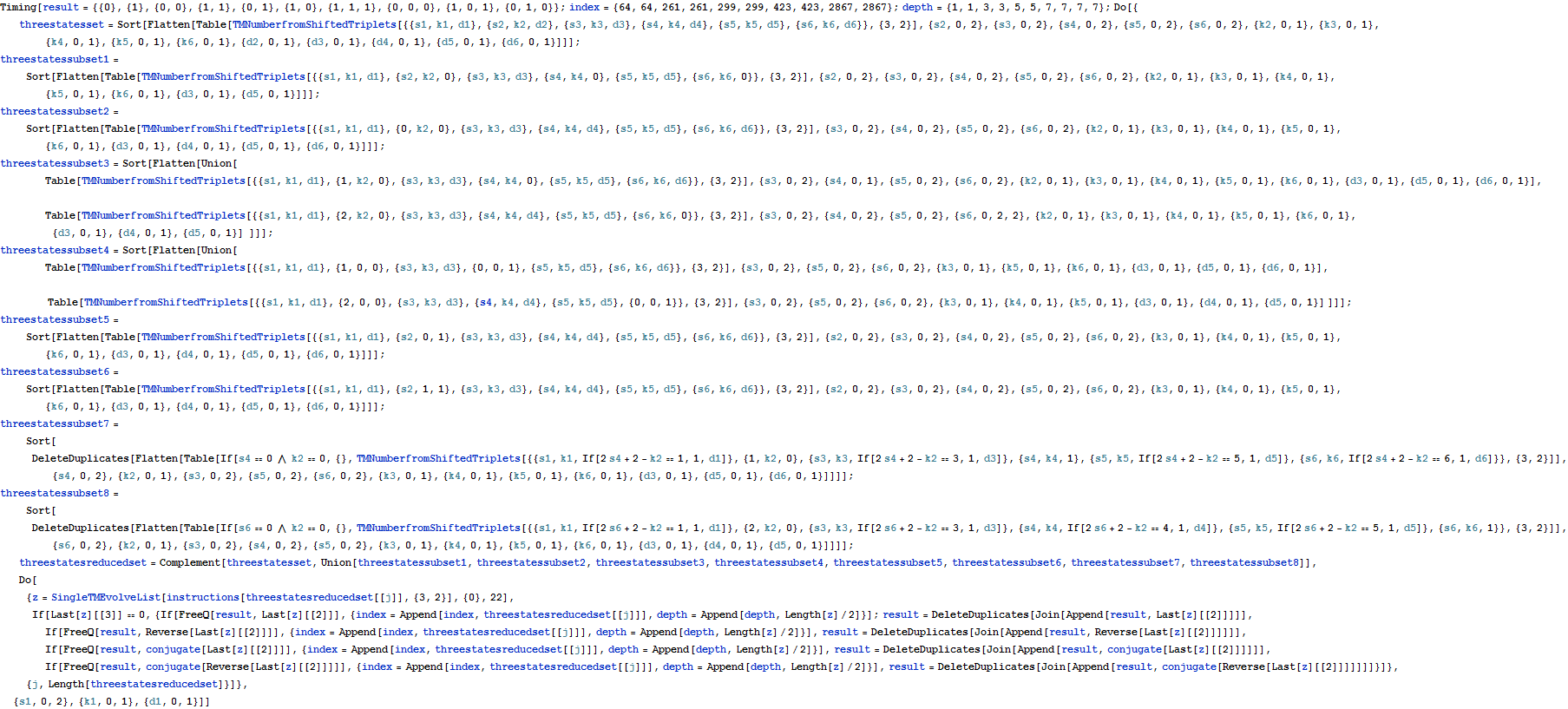
Search for new sequences :
![]()
![]()
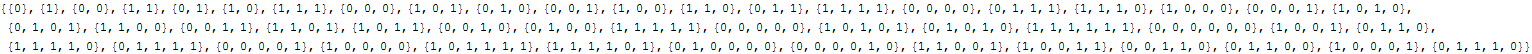
![]()
![]()
![]()
![]()
![]()
![]()

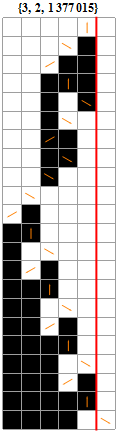
![]()
Analysis of the 4294967296 4-states binary machines (Incomplete).
Activation of preliminary instructions :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Search for new sequences :

![]()
![]()

![]()
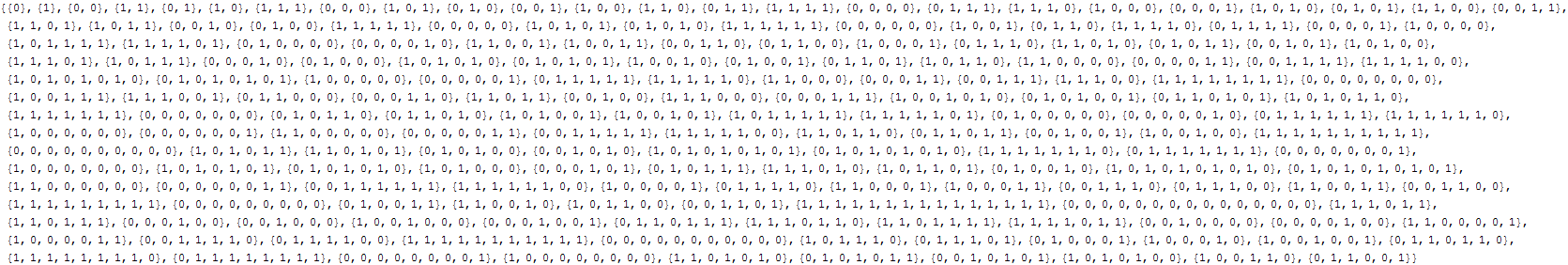
![]()
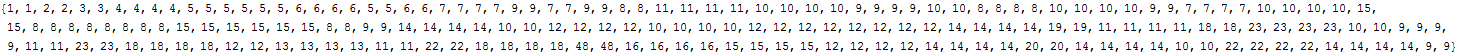

![]()

![]()

2. Modified numbering scheme of Turing machines with s states and k characters, half infinite tape and no explicit halting state.
Once s and k are known, their exist 2s k distinct triplets (numbered from 0 to 2s k - 1) :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
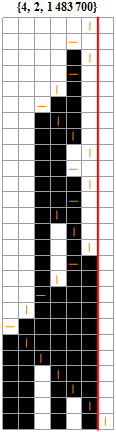
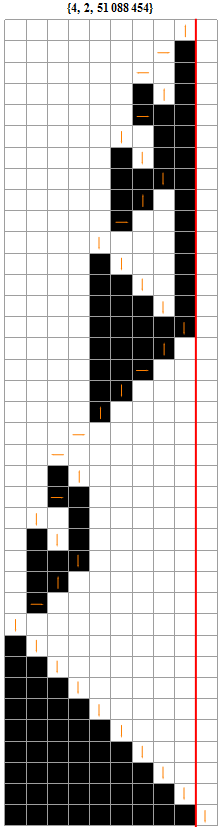
Running a particular machine (new numbering !) :


![]()
Even on a multi core PC Mathematica is unable to run 4294967296 machines in a reasonable time (a few days are needed). A C++ program is much more rapid and GPU programming helps a lot : a few minutes suffice !
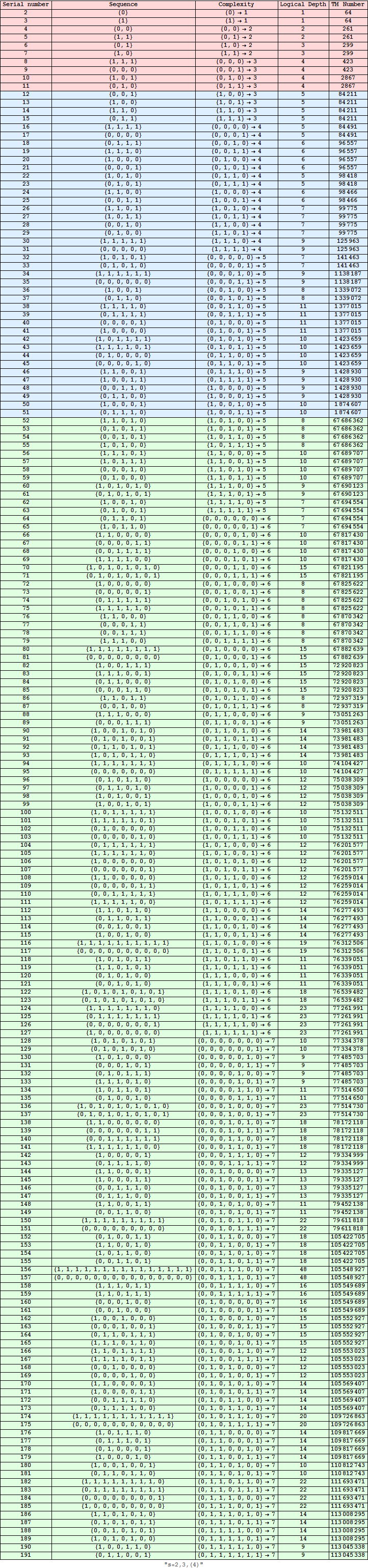
Treatment of the sequences output by 4-states binary TM (Parallelized in C++ : MT4_cuda.exe -> MT4.txt).
Reading the output file in Mathematica ({Machine number, number of steps, printed sequence}) :
![]()
![]()

Busiest beaver :
![]()
![]()
![]()
![]()
Most productive beaver :
![]()
![]()
![]()
![]()
{Machine number, logical depth, printed sequence} :
![]()

Symmetrization and reordering of the results (sequence, reversed sequence, conjugate sequence and reversed conjugate sequence) :
![]()
![]()

![]()
![]()

![]()
![]()