Walsh functions and lossy compression.
Walsh functions are best introduced via Hadamard matrices.
Hadamard matrices :
![]()
![]()
![]()
![]()
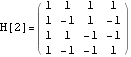
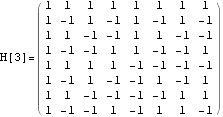
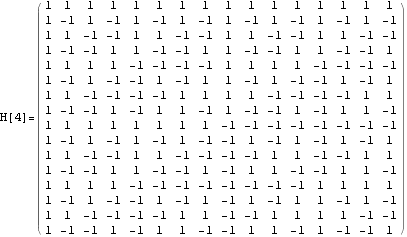
Walsh-1D functions :
Walsh functions are given by the rows (equivalently the columns) of the Hadamard matrices.
![]()
Two examples : s = 3 (8 functions) and s = 4 (16 functions) :
![]()
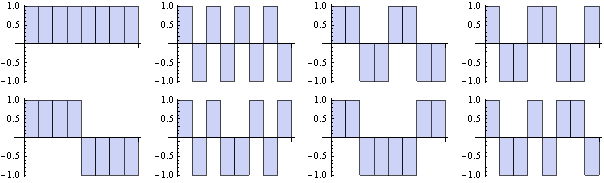
![]()
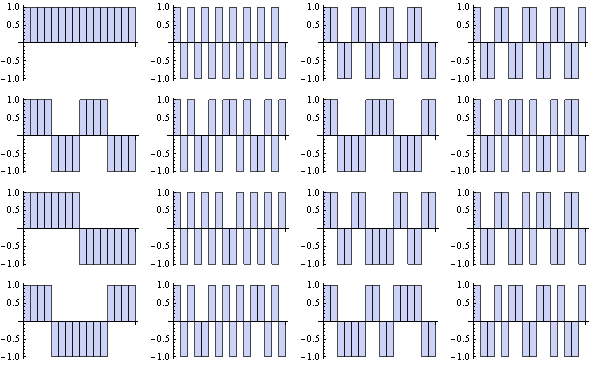
Walsh functions are orthonormed with respect to the following scalar product :
![]()
![]()
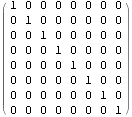
An arbitrary binary 1D-function (say {1,1,1,1,1,1,-1,-1} if s = 3) is expandable in the basis of 1D-Walsh functions :
![]()
![]()
Walsh-2D functions :
![]()
![]()

The following character, R, is pixellized in a 64x64 grid :
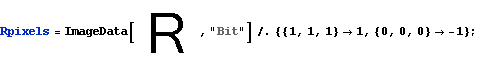
![]()
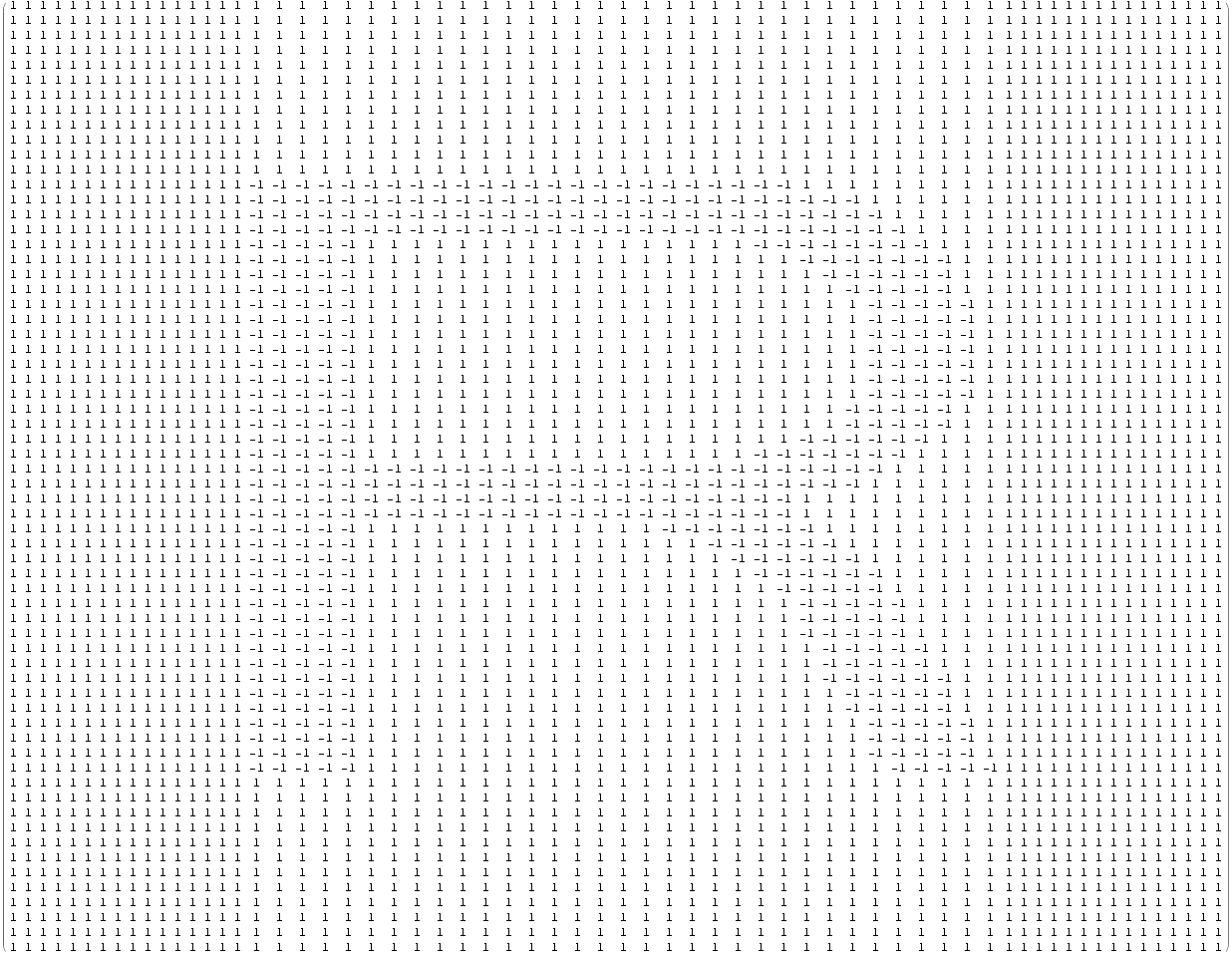
![]()
![]()
The walsh coefficients for the letter R :
![]()
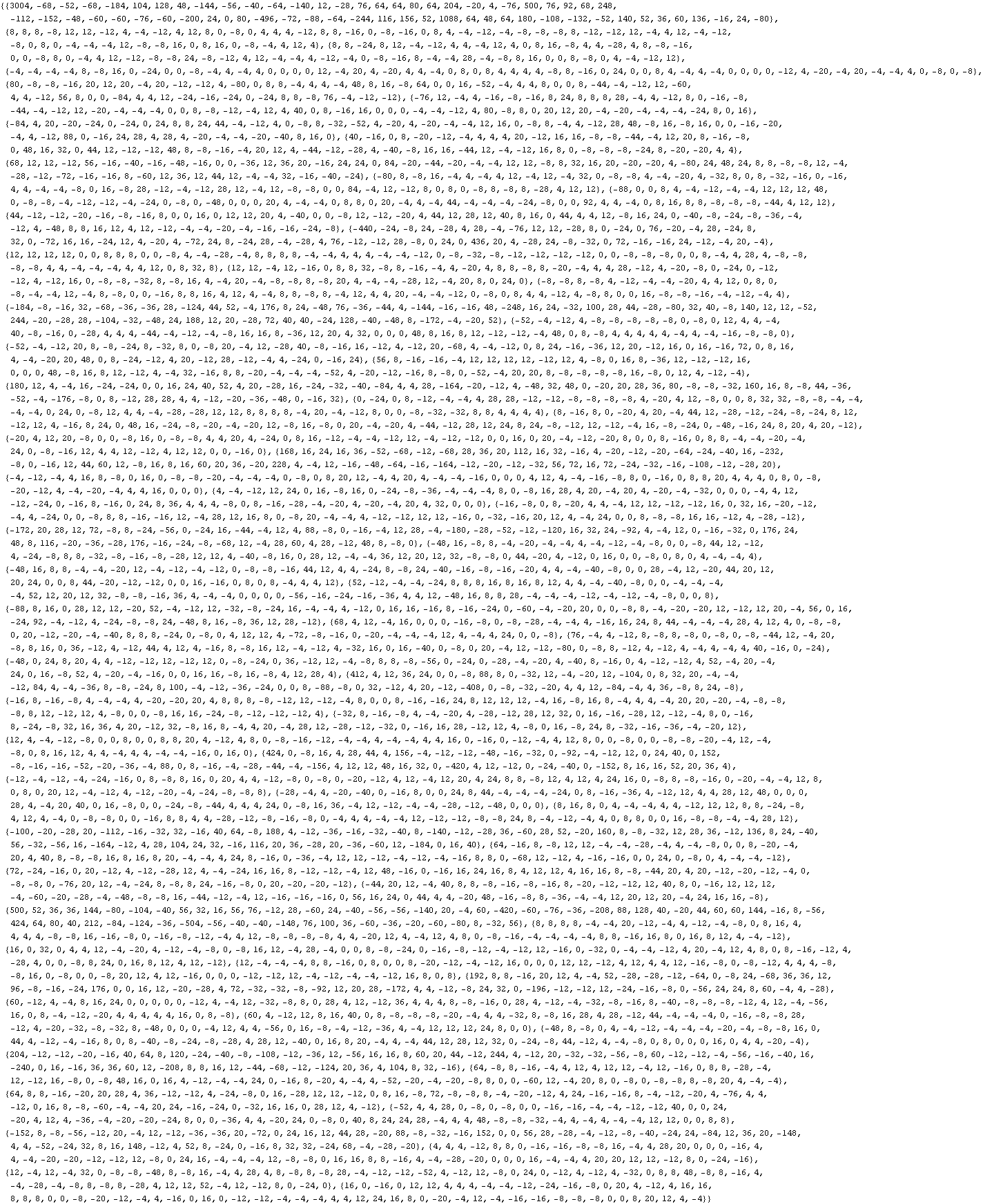
The walsh coefficients for the letter R, sorted in decreasing order (absolute value) :
![]()
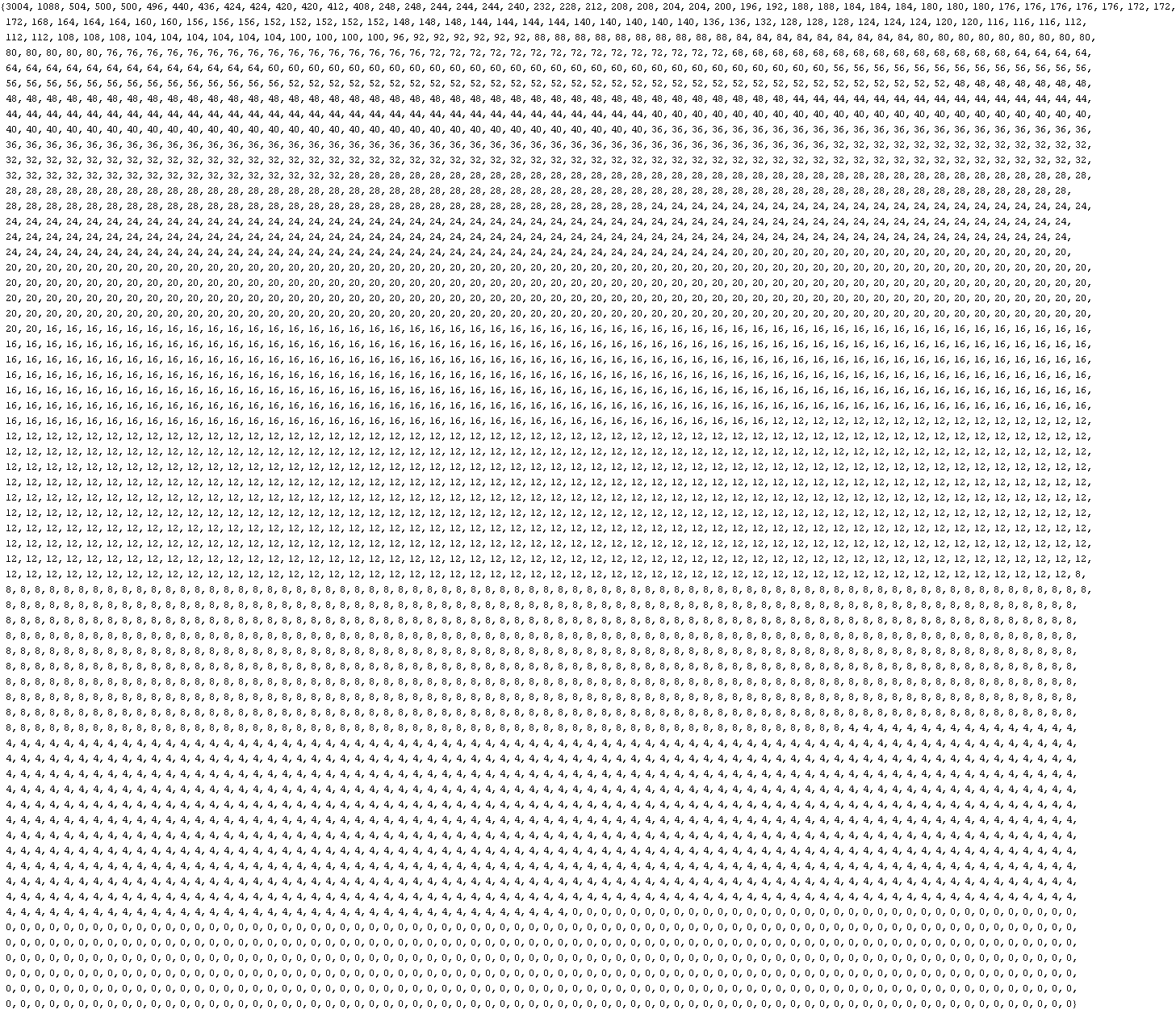
An arbitrary binary 2D-function (say Rpixels) is expandable without loss in the basis of 2D-Walsh functions :
![]()
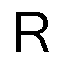
![]()
![]()
Light truncation :
![]()
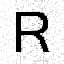
![]()
![]()
Light truncation with greylevels erased :
![]()
![]()
![]()
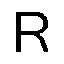
Medium truncation :
![]()
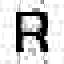
![]()
![]()
Medium truncation with greylevels erased :
![]()
![]()
![]()
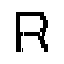
Strong truncation :
![]()
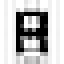
![]()
![]()
Strong truncation with greylevels erased :
![]()
![]()
![]()