Phys
Quelques problèmes de physique, instructifs, curieux ou amusants
Sommaire
[ afficher ]- Chandelle à bascule
- Capture d'une balle
- Equilibre stable
- Moteur simplissime
- Synchronisation spontanée
- Bachelier, où est la faille ?
- Billard rectangulaire, classique et quantique
- Heurs et malheurs du boson de Higgs
- Dynamique intégrable ou chaotique d'un billard convexe
- Variations sur le thème du gaz de Szilard
- Compressions astronomiques : Hipparque contre Newton
- Chorégraphies classiques
- Chute libre relativiste
- Attraction universelle
- Galilée versus Lorentz
- Le faux paradoxe des vrais jumeaux
- Optique quantique, un bel exemple de pléonasme
- Réflexion sur un miroir mobile
- Expériences par la pensée en relativité restreinte
Cette section, en construction permanente, présente des expériences ou des problèmes de physique, vus par le petit bout de la lorgnette.
Capture d'une balle
Pour des détails techniques concernant le mouvement d'une particule pesante, assujettie à se mouvoir sur une surface imposée, voir ici (Notebook Mathematica).
Synchronisation spontanée
Cette expérience, futile en apparence, pourrait suggérer que l'on dispose les sections de 1er et de seconds violons, d'altos et de violoncelles des orchestres symphoniques, sur des plates-formes posées sur rouleaux afin d'obtenir que les musiciens jouent enfin de concert !
Bachelier, où est la faille ?
La présentation d'un problème recourt parfois à des simplifications - louables, à première vue - qui sont de nature à désorienter sinon fourvoyer le lecteur. Quel étudiant universitaire en sciences démêlerait rapidement (et même lentement !) le pseudo-paradoxe suivant ?
Un véhicule, de masse m, animé de la vitese v0 par rapport au sol, atterrit tangentiellement, touchant le sol à l'instant t = 0. Les freins ayant été préalablement bloqués, il s'immobilise bientôt sous l'effet des forces de frottement. Son énergie cinétique passe donc de la valeur classique, Kin = m v02/2, à la valeur Kfin = 0. Cette énergie n'a pas disparu pour autant, elle se retrouve (intégralement ? pas si sûr, cfr infra) sous forme de chaleur, Q, dissipée dans les pneumatiques et le sol. Jusque là, tout semble aller bien. Là où les choses paraissent se corser, c'est lorsqu'on observe la scène dans le référentiel (inertiel, comme celui lié au sol), animé de la vitesse v0 par rapport au sol. On serait tenté de raisonner comme suit : le véhicule passe de la vitesse nulle à la vitesse -v0 donc il acquiert une énergie cinétique, m v02/2 (c'est correct). D'où vient cette énergie, sûrement pas des freins qui se refroidissent !
Solution. Le piège se situe au niveau d'une hypersimplification de l'énoncé, renforcée par le dessin suivant , qui sème le trouble. La conservation de l'énergie ne se conçoit que dans un système isolé et le fait est que le système représenté à gauche ne l'est qu'imparfaitement. Considérer que le sol est rivé à une terre immobile donc qu'il n'intervient pas dans le bilan énergétique est faux : on s'en rend compte en remaniant le dessin comme représenté à droite.

Le recul du sol doit être pris en compte et c'est ce que la figure de droite représente en posant ce sol sur une surface de base sans frottement. A présent les bilans énergétiques s'établissent comme suit, selon le référentiel dans lequel on travaille :
- Dans le référentiel absolu, S, on a que les vitesses des masses m et M évoluent selon les lois, v = v0- (f/m) t et V = 0 + (f/M) t. L'instant final, tfin = Mm v0/[(M+m)f], est celui où la vitesse relative de m par rapport à M devient nulle (V=v). A cet instant, l'ensemble, M+m, se déplace à la vitesse m v0/(M+m). Le bilan énergétique se détermine comme suit : à l'instant initial, tin = 0, Ein = K(m) + K(M) = m v02/2 + 0 et à l'instant final, tfin = Mm v0/[(M+m)f], Efin = K(m) + K(M) + Q = 0 + m2 v02/[2(M+m)] + Q.
La quantité de chaleur dissipée, Q, vaut le travail de la force de frottement lors du mouvement relatif des surfaces,Au bilan et après simplifications, on a que l'énergie se conserve sous la forme, Ein = Efin. Bien noter que ce bilan ne dit pas tout à fait que la quantité de chaleur dissipée vaut l'énergie cinétique initiale de m car la terre, en reculant, emporte une partie microscopique de l'énergie (le rapport m/M est ridiculement petit) mais c'est cette différence qui règle son compte au pseudo-paradoxe. Voyons cela de plus près en raisonnant dans le référentiel en mouvement, S'.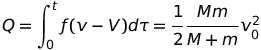
- Dans le référentiel, S', animé de la vitesse, v0, par rapport à S, les vitesses évoluent selon les lois, v = 0 - (f/m) t et V = -v0 + (f/M) t. L'instant final, tfin = Mm v0/[(M+m)f], n'a pas changé, se calculant comme dans S. De même, la quantité de chaleur dissipée, Q, vaut encore, Q = Mm v02/[2(M+m)]. Le bilan énergétique se détermine comme suit : à l'instant initial, tin = 0, Ein = K(m) + K(M) = 0 + M v02/2 et à l'instant final, tfin = Mm v0/[(M+m)f], Efin = K(M+m) + Q = M2 v02/[2(M+m)] + Mm v02/[2(M+m)] = M v02/2 = Ein. L'énergie est bien conservée et la contradiction disparaît. Autrement dit, l'énergie se conserve dans ce référentiel mais il faut tenir compte du recul de la terre ! C'était déjà le cas dans S mais cette subtilité n'y jouait pas un rôle aussi apparent.
- Le bachelier vraiment très curieux souhaitera peut-être vérifier la conservation de l'énergie dans le référentiel (non inertiel !), lié à la masse m. La deuxième loi de Newton continue de s'appliquer, dans ce référentiel, à condition de considérer qu'un champ fictif d'inertie y règne, indiscernable d'un champ de gravitation, g = f/m, orienté en sens contraire de l'accélération absolue de m, soit de gauche à droite sur la figure. Le bilan énergétique doit, cette fois, prendre en considération qu'une énergie potentielle de type, mgh, est associée à ce champ. La masse m est solidaire du référentiel non inertiel donc son énergie cinétique est nulle à tout instant. On peut en dire autant de l'énergie potentielle puisque la position de m est évidemment invariable par rapport à elle-même (mgh = 0 car h = 0). En définitive, le bilan énergétique ne fait intervenir que M et Q. En détail, l'énergie cinétique de M diminue de la valeur Kin = M v02/2 à la valeur Kfin = 0. L'énergie potentielle augmente (car en mouvement relatif, M se déplace vers la gauche par rapport à m (il remonte les lignes de champ), d'une quantité égale à M gfictif h = M (f/m)(em-eM) = M2 v02/[2(M+m)]. Au bilan, on vérifie que l'on a bien : M v02/2 - M2 v02/[2(M+m)] = Mm v02/[2(M+m)] = Q, comme il se doit. On note que Q possède la même valeur dans tous les référentiels considérés.
Billard rectangulaire, classique et quantique
Les billards considérés par les mathématiciens et les physiciens ont peu de points communs avec le divertissement bien connu : ils considèrent habituellement des aires planes, limitées par une courbe périmétrique simple (= sans point multiple) et convexe (= toute droite du plan coupe la courbe en moins de 3 points). Les points anguleux sont autorisés (comme dans les billards polygonaux) et certains auteurs étudient même des situations plus complexes qui ne nous concernent pas ici (billard à 2 dimensions sur une surface non plane, billard à 3 dimensions, billards en présence d'un champ de gravité actif (non orthogonal à la table), etc. Les règles de ce jeu idéal sont faciles à comprendre : tout point matériel, qui se déplace sans frottement sur la table, se réfléchit sur le périmètre en respectant la loi de l'optique géométrique. Dans le cas des billards polygonaux, on peut ajouter cette règle que tout point atteignant un coin rebondit en revenant sur ses pas.
Aussi étonnant que cela puisse paraître, beaucoup de questions élémentaires relatives à des billards très simples ne sont toujours pas élucidées. Par exemple, l'(in)existence de trajectoires périodiques dans un billard triangulaire obtusangle n'est pas démontrée lorsqu'on exclut les coins. La même question est, par contre, facile à résoudre dans le cas du billard rectangulaire grâce au fait qu'on peut indéfiniment paver le plan à l'aide de rectangles identiques. Voici pour fixer les idées, quelques trajectoires périodiques dans un rectangle dont les côtés ont été choisis égaux à a=2 et b=1 (exigez un va-et-vient complet dans les deux premiers exemples !) :

Commençons par chercher toutes les trajectoires périodiques en les classant dans l'ordre des longueurs croissantes. L'intérêt de la solution à cette question apparaîtra lorsqu'on passera au billard quantique. Une procédure est connue qui résout la question posée de façon particulièrement élégante.
Pour déterminer la trajectoire suivie par le point mobile lorsqu'on le lance à partir d'un point quelconque, disons, (x=0.7, y=0.3), on pourrait calculer les rebonds successifs sur les côtés du rectangle; c'est possible mais c'est fastidieux et il y a beaucoup mieux à faire. On commence par paver le plan par des copies du rectangle de base comme l'indique la figure suivante. Dans chaque nouveau rectangle ainsi défini, on pose, de proche en proche, que les points homologues au point de départ sont situés symétriquement par rapport au côté qui les sépare. La figure représente quelques copies du rectangle primitif et les points homologues (seuls les points noirs importent à ce stade de l'exposé). En développant un minimum de géométrie élémentaire, on se convainc aisément que tout segment de droite qui joint le point initial à l'un quelconque de ses homologues représente le déplié exact d'une trajectoire brisée fermée (revenant au point de départ). La figure en représente deux, à titre d'exemple : le segment noir horizontal est le déplié de la trajectoire qui revient au point de départ après un seul rebond sur le côté droit. Le segment noir oblique est le déplié d'une trajectoire qui subit autant de rebonds qu'il y a d'intersections avec les joints du pavage, soit 6. Le lecteur est invité à redessiner mentalement la trajectoire réelle dans le rectangle primitif.
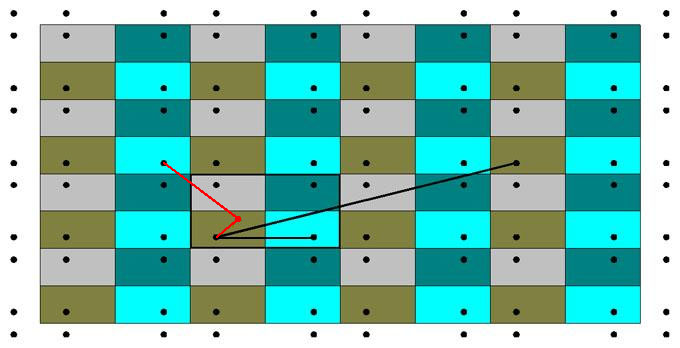
Cette procédure permet de faire l'inventaire complet des trajectoires fermées, celles qui reviennent au point de départ. Elles ne sont pas nécessairement périodiques car pour qu'elles le soient, il faut encore s'assurer que la vitesse finale du point est orientée comme à l'instant initial et ce n'est le cas que pour le deuxième exemple considéré. C'est ici qu'intervient le coloriage du pavage. On note que les rectangles ont été regroupés 4 par 4, chaque couleur correspondant à une orientation différente du vecteur vitesse (il n'y en a que 4, d'où les 4 couleurs). Pour que la trajectoire soit périodique, il faut que le point homologue final soit positionné dans un rectangle de même couleur que le point initial. Si l'on note (x0, y0), les coordonnées du point initial, les points homologues se notent : (±x0 + 2j a, ±y0 + 2k b), pour j, k = 0, ±1, ±2,, ... ). Ceux qui appartiennent à un rectangle de même couleur que lui se notent : (x0 + 2j a, y0 + 2k b). La longueur des trajectoires périodiques s'en déduit :
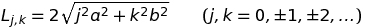
soit : {2, 4, 4.47214, 5.65685, 6, 7.2111, 8, 8.24621, 8.94427, 10, 10.7703, 11.3137, 12, ...}, dans l'exemple, a=2 et b=1, et quelles que soient les coordonnées du point de départ.
Il existe un rapport surprenant entre la liste des Lj,k et celle des énergies quantifiées du même billard, quantique cette fois. Il s'agit d'un billard nanoscopique, où la particule se déplace à une vitesse de l'ordre de ℏ/(μ a).
Le billard quantique rectangulaire est assimilable à un puits de potentiel nul, flanqué de parois "verticales" infinies donc infranchissables. Cette fois toutes les vitesses ne sont plus autorisées surtout pas la vitesse nulle, ce qui serait en contradiction avec le principe d'incertitude : seules certaines vitesses sont possibles donc certaines énergies (cinétiques puisque le potentiel est nul dans l'enceinte du billard). Les états permis sont solution de l'équation de Schrödinger, flanquée des conditions aux limites sur les bords du billard :
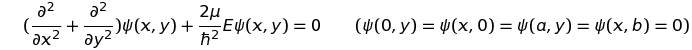
La solution de cette équation est classique (m, n = 1, 2, 3, ...) :
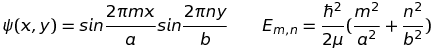
Dès les premiers pas de la mécanique quantique, vers 1913, on a cherché l'hypothétique moyen de relier les trajectoires classiques aux états quantiques quitte à y adjoindre une condition de quantification évidemment absente de la théorie classique. Ce fut l'idée qui prévalut lors de la conception de la première mécanique quantique de Bohr & Sommerfeld : ils ont proposé de ne retenir que les trajectoires périodiques dont l'intégrale d'action était un multiple de la contante (réduite) de Planck. Ce procédé a vite connu ses limites, singulièrement lorsque le système étudié exhibait une dynamique chaotique. Il est dès lors tombé en désuétude jusqu'à ce que son fantôme ressuscite sous une forme étonnante, suite aux travaux de Martin Gutzwiller, en rapport avec l'approximation semi-classique. Voici quelques éléments simplifiés à l'extrême et de nature à initier l'amateur distingué. On considère la fonction suivante (pour rappel, E=p2/(2μ)) :
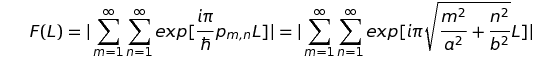
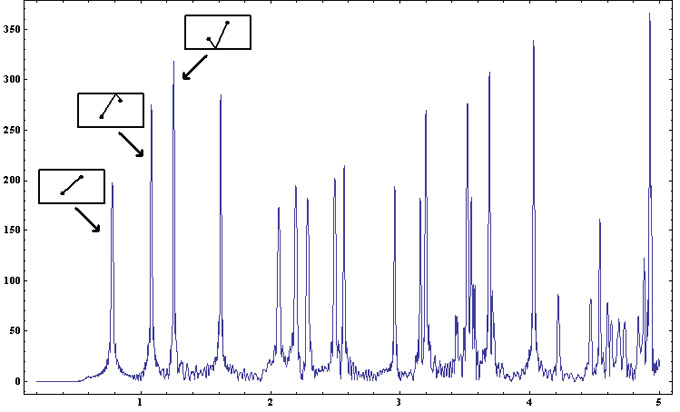
Le graphe de cette fonction présente des pics bien visibles dont les positions coïncident avec les longueurs des trajectoires périodiques prises dans l'ordre croissant, soit aux valeurs déjà trouvées, {2, 4, 4.47214, 5.65685, 6, 7.2111, 8, 8.24621, 8.94427, 10, 10.7703, 11.3137, 12, ... .
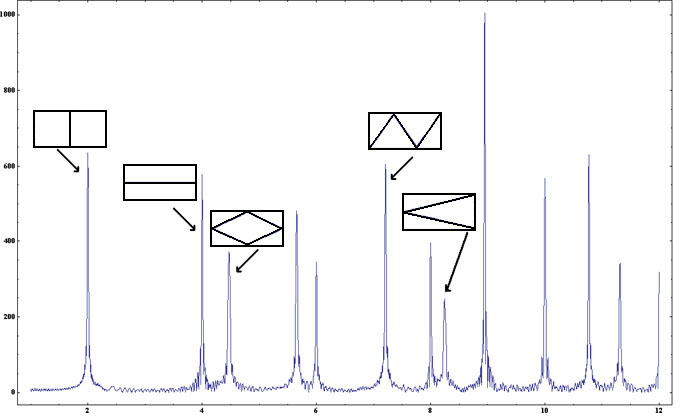
Ceci n'est pas un hasard : on peut effectivement retrouver les longueurs des trajectoires périodiques d'un billard classique à partir des états quantifiés d'énergie (donc de quantité de mouvement puisque le potentiel est nul à l'intérieur du billard) du billard quantique correspondant. Le lecteur motivé s'en assurera sur le billard circulaire voire elliptique.
(In)formellement, on note que F(L) n'est rien d'autre que la transformée de Fourier de la densité de quantité de mouvement, g(p) :
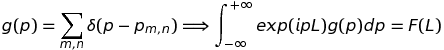
On s'attend dès lors à ce que la transformée de Fourier inverse permette de repasser de F(L) à g(p) :
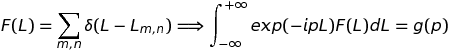
Autrement dit, connaissant les longueurs des trajectoires périodiques du billard, on pourrait espérer reconstruire le spectre quantique de quantité de mouvement, donc d'énergie. C'est possible dans le cas du billard rectangulaire et il n'est pas nécessaire de se lancer dans de savants calculs pour s'en convaincre car on a, par transformée de Fourier :
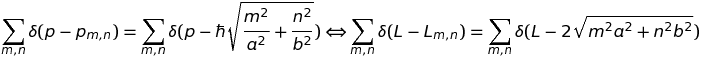
Le seul point délicat concerne les domaines de parcours des indices, m et n, qui ne sont pas absolument identiques, 0 étant exclu dans les niveaux d'énergie alors qu'ils sont autorisés dans les longueurs de trajectoires (sauf m=n=0). La conséquence est la présence de pics parasites dans le spectre d'énergie. Voyons cela de plus près. On considère la fonction,
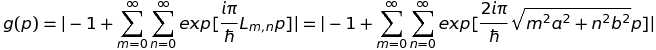
Son graphe présente les pics espérés plus des pics surnuméraires correspondant à de faux états quantiques (m = 0 ou n = 0, non physiques car la fonction d'onde serait nulle) :
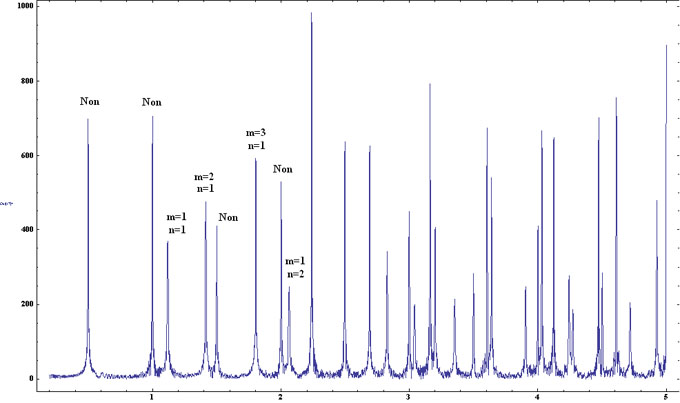
Revenant à la fonction, F(L), montrons que les coïncidences ne s'arrêtent pas là. Si on généralise F(L) en incorporant la fonction d'onde calculée en un point quelconque du billard, par exemple, (x1=0.7, y1=0.3),
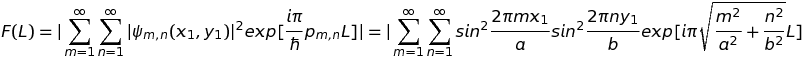
On trouve un graphe du même genre que précédemment sauf qu'il présente des pics correspondant aux trajectoires fermées (non nécessairement périodiques) passant par ce point :
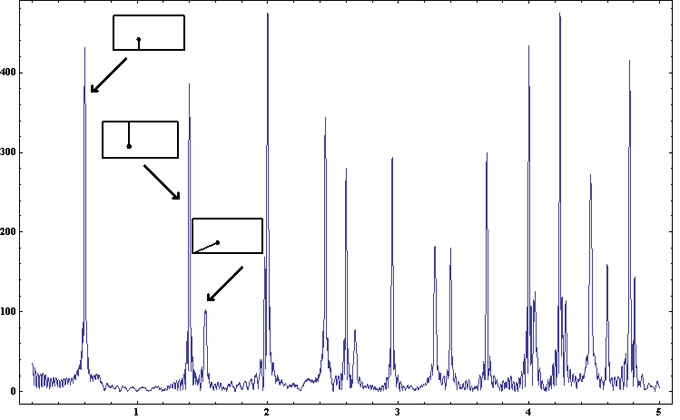
On peut encore aller plus loin en sélectionnant deux points quelconques sur le billard, par exemple, (x1=0.7, y1=0.3) et (x2=1.3, y2=0.8). Cette fois on construit la fonction,
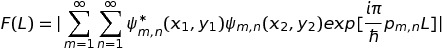
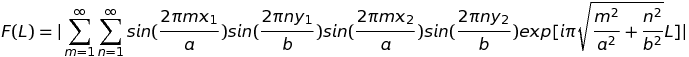
On obtient le graphe suivant où les pics correspondent, dans l'ordre des longueurs croissantes, aux trajectoires ouvertes qui relient les deux points. Le premier pic correspond à la plus courte d'entre elles soit le segment de droite joignant les deux points. On peut facilement dresser l'inventaire de toutes ces trajectoires ouvertes en ajoutant le point, (x2=1.3, y2=0.8), sur le rectangle primitif de la première figure ci-dessus (ce point y est représenté en rouge). Les trajectoires déployées s'obtiennent en joignant ce point à (x1=0.7, y1=0.3) et à tous ses homologues. Les trajectoires réelles s'en déduisent par repliement.
Heurs et malheurs du boson de Higgs
Le CERN de Genève nous a une nouvelle fois gratifié d'un de ces effets de manche dont il est coutumier (cfr les neutrinos supra-luminaux) en annonçant la mise en évidence expérimentale de l'hypothétique boson de Higgs. En fait d'événement, il s'agit plutôt d'un non-événement : il y a belle lurette que le modèle standard a intégré l'existence de cette particule dont le champ est sensé conférer la masse à toutes les autres. A cet égard, l'événement eut été que ce boson n'existât pas.
Les mathématiciens sont logés à la même enseigne depuis plus d'un siècle que Riemann a conjecturé que les zéros non triviaux de la fonction Zêta sont tous situés sur la droite, Re[z]=1/2 : le scoop - et le pavé dans la mare ! - serait que cette conjecture soit fausse car les énoncés abondent qui commencent par la sentence "Sous réserve que l'hypothèse de Riemann soit correcte, alors on a ...".
Si ce boson existe avec une probabilité de 99.99 % (dixit le communiqué du CERN, drôle d'usage de la notion de probabilité mais, j'en conviens, c'est un autre débat), la physique ne s'en trouve pas plus avancée pour autant. Le moins que l'on puisse demander à une particule qui confère sa masse à toutes les autres est qu'elle explique pourquoi le proton est 1836 fois plus massif que l'électron et le neutron 1838 fois. Or cela, elle ne le peut pas et ne le pourra vraisemblablement jamais car si cette prouesse était réalisable, il y a longtemps qu'elle aurait été accomplie. On en revient toujours au même point : le modèle standard est très loquace quand il n'y a rien à calculer de précis mais parfaitement muet quand il s'agit d'expliquer le résultat de mesures précises parfois au-delà du milllionième. Cette critique n'est pas neuve, Feynman la sous-entendait déjà dans les années 1980, pointant du doigt que le modèle standard ne respectait pas le protocole physique idéal, rappelé ci-après.
Alors que les mathématiciens vivent dans un monde confortable où tout système axiomatique non contradictoire est digne d'étude, les physiciens vivent dans le monde réel et à la contrainte de non contradiction s'ajoute celle de ne retenir que les axiomes compatibles avec les observations faites. C'est une quête sans fin "à l'envers" : on ne pose pas les axiomes afin de les développer, on tente de remonter des faits observés et mesurés aux axiomes, ce qui est très différent.
Selon Feynman, la physique progresse idéalement en trois étapes dans un ordre déterminé :
- Elle observe les phénomènes et en mesure certains paramètres objectifs.
- Elle cherche un modèle mathématique (une formule "toute faite", une équation différentielle, un programme informatique, ... ) capable de restituer ces données expérimentales.
- Elle affine une interprétation du modèle, en langue vulgaire, essentiellement destinée à permettre de le diffuser et de l'enseigner. Tout nouvel ensemble de mesures exige éventuellement une réactualisation du modèle ou de l'interprétation.
Il est faux de croire qu'il n'existe qu'un seul modèle capable de restituer un ensemble de données. Il peut en exister beaucoup, asymptotiquement tangents, même s'il il est vrai que toute nouvelle acquisition de données peut éventuellement disqualifier certains d'entre eux.
Toute l'histoire du modèle standard est en rupture avec ce protocole car la théorie y a toujours dicté sa loi à l'expérimentation. Un grand nombre de grandeurs "mesurées" - par exemple des paramètres de désintégration - ne sont que des variables définies par un modèle qui croit en leur existence et la justifie au motif que l'ajustement des données expérimentales a fourni un intervalle de confiance pour sa valeur numérique. Qu'un tel ajustement fournisse une valeur particulière ne nous apprend rien car la méthodologie suivie est circulaire.
Les deux nucléons (proton et neutron) sont les deux particules les mieux mesurées au plan de leur masse, m, et de leur moment magnétique, μ. On connait :
Aucun modèle, fut-il standard (sous-entendu, reçu par la communauté scientifique), ne peut se targuer de quelques succès que ce soit s'il n'est pas capable de rendre compte de ces valeurs avec un degré de précision convenable. Voici un modèle arithmétique qui ne prétend nullement être parfait mais qui possède, au moins, cette vertu. Il a été publié pour la première fois, en 1965, par Antoine Hautot, Professeur de Physique à l'Université de Liège (Bull. Soc. Roy. Sci. Liège, Vol. 34 (pp 97 et suiv.) et j'y ai ultérieurement collaboré dans quelques essais rétrospectifs (Physics Essays : 5 (1992), pp 90-96 et 9 (1996), pp 159-185). Ce modèle, basé sur une arithmétique élémentaire, est bien trop précis pour qu'il souffre d'un hasard numérologique. Voici quelques règles simples sur lequel il repose :
- La masse est quantifiée et le quantum de masse vaut la mase de l'électron : me = 1 qm.
- Les quanta de masse sont usuellement groupés en couches numérotées par un entier, n, pouvant prendre toutes les valeurs entre 1 et 7 (incluses). Une couche de rang n contient exactement 16 n2 qm (Cette loi correspond à l'empilement non dense de sphères autour d'une sphère centrale). Voici le détail des populations autorisées pour les couches : 16, 64, 144, 256, 400, 576 et 784 (qm).
- Toute particule est formée de couches assemblées éventuellement autour d'un quantum central. La masse réelle de la particule est inférieure à la masse numérique, M, ainsi définie, du fait de l'existence d'une énergie de liaison, valant, en première approximation, -M/784.
Un modèle numérique ne se discute pas : il fonctionne ou il ne fonctionne pas et il n'est pas question de l'écarter au seul prétexte qu'il est incompatible avec une théorie pré-existante - le modèle standard - qui échoue précisément à expliquer les mêmes données. Autrement dit, on ne juge pas de la valeur d'une théorie à la lumière d'une autre.
Avant de tester ce modèle arithmétique sur le nucléon, observons comment il se débrouille avec les mésons les mieux connus, μ, π et K :
Le cas des nucléons est encore plus impressionnant. Leur structure numérique de base est identique, à un détail près :
- Neutron (un quantum central plus les couches, n = 1, 2, 3, 4, 6 & 7) : 1 + 16 + 64 + 144 + 256 + 576 + 784 = 1841 qm.
- Proton (un quantum central plus les couches, n = 1, 2, 5, 6 & 7) : 1 + 16 + 64 + 400 + 576 + 784 = 1841 qm.
On trouve les moments magnétiques, en première approximation, en considérant que seuls le quantum central et les couches impaires (1 + 16 + 144 + 784 = 945) du neutron sont spinales et paires (1 + 64 + 576) = 641 dans le cas du proton. Les moments s'en déduisent sur base de la formule classique, μ = mp/mspinale (μN) :
Telles sont les données brutes qu'un simple modèle arithmétique révèlent instantanément. Elles peuvent être améliorées et elles l'ont été dans le cadre d'une théorie interprétative exposée dans les articles cités en référence. Celle-ci ne prétend nullement être "vraie" en l'état mais il est tout-à-fait envisageable que de réels progrès suivraient si seulement les chercheurs déployaient, dans cette direction, la même ardeur qu'ils ont mise, souvent à perte, au service du modèle standard depuis 50 ans. Rien n'exclut d'ailleurs que les modèles standard et arithmétique, a priori si éloignés, se rejoignent un jour.
Dynamique intégrable ou chaotique d'un billard convexe
Le billard plan des physiciens est une table horizontale, limitée par un contour fermé, sur laquelle évolue un point matériel selon une suite de mouvements rectilignes uniformes. Lorsque la trajectoire atteint la frontière du billard, le rebond s'effectue conformément à la loi de la réflexion en optique géométrique (l'angle d'incidence vaut l'angle de réflexion). Nous nous limitons ici aux billards convexes, ceux que toute droite sécante ne coupe, au plus, qu'en deux points. Nous ne considérons donc pas les billards concaves ni les billards limités par une courbe non simple. On illustre ces différences sur l'exemple du billard limité par la courbe d'équations paramétriques,
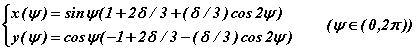
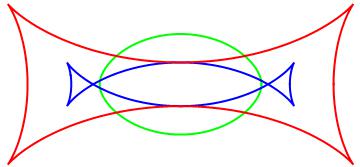
δ=2 : billard non simple (bleu)
δ=4 : billard concave (rouge)
Le repérage des rebonds successifs sur la frontière du billard n'est commode dans aucun système de coordonnées usuels (cartésiennes ou polaires). Pour une gestion numérique agréable de ces rebonds, il est préférable d'investir dans un système de coordonnées angulaires (ψ, α) ou, ce qui revient au même, dans le système dérivé (s, p), tous deux définis ci-après.
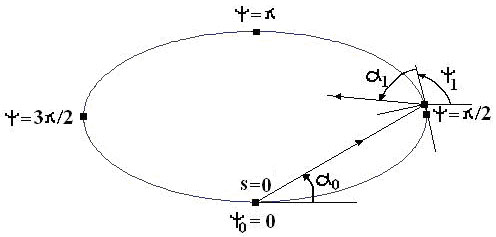
ψ, mesure, en tout point, l'angle que fait la tangente positive à la courbe avec l'axe horizontal positif (Ox). α, mesure l'angle que fait la trajectoire issue du rebond avec la tangente positive avec en ce point. On remplace avantageusement l'angle, α, par son cosinus, noté p, et l'angle, ψ, par la longueur d'arc mesurée à partir du point de référence, ψ=0, nécessairement situé au point le plus bas. L'espace des phases (s, p) occupe le domaine, (0, L)x(-1,+1), où L est le périmètre du billard. En résumé :
- Si R(ψ) désigne le rayon de courbure de la frontière au point, ψ, on a que :
-
-
l'arc séparant le point, ψ, de l'origine vaut :
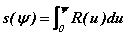
-
les coordonnées cartésiennes du point, ψ, sont données par :
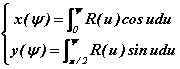
-
les coordonnées des rebonds successifs se calculent récursivement, (αi, ψi) → (αi+1, ψi+1), en résolvant (numériquement) le système :
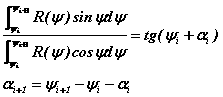
-
l'arc séparant le point, ψ, de l'origine vaut :
1. Un billard intégrable : le billard elliptique d'équation cartésienne
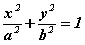
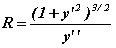
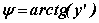
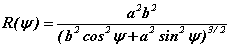
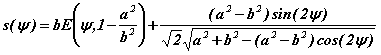
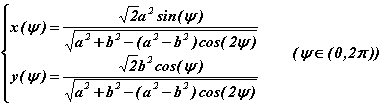
Considérons l'exemple, a=2, b=1. La figure suivante présente 9 trajectoires correspondant aux conditions initiales, ψ0= 0, π/6 et π/3 et α0= 1, 3/2 et 2. Le point de départ est noté en gras et l'itération porte sur 20 rebonds successifs. La figure suivante montre le portrait de phase (s, p) dans chaque cas :
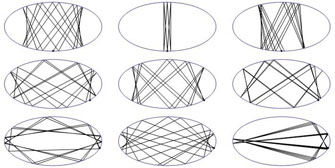
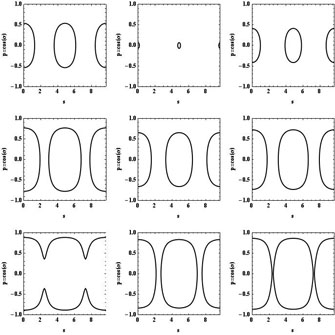
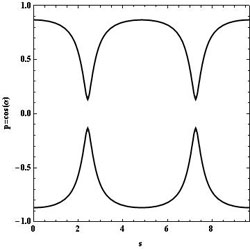
Le portrait de phase complet est constitué de l'infinité non dénombrable des trajectoires de phase qui couvrent densément le plan (on n'en a dessiné que quelques-unes) :
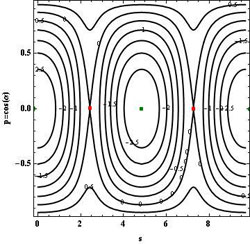
Ce portrait est simple parce que le billard elliptique est intégrable : on signifie par là que les coordonnées des rebonds successifs sont reliées entre elles par une relation analytique (on parle d'invariant) qui limite les évolutions possibles aux trajectoires régulières périodiques (rarement) ou quasi-périodiques (le plus souvent). Cet invariant se note :
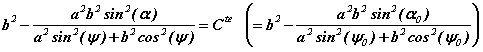
Chaque courbe du portrait de phase est une courbe de niveau de cet invariant dont la valeur constante est déterminée par le choix des conditions initiales. Il y a une infinité non dénombrable de conditions initiales qui respectent une même valeur de la constante et chacunes d'elles engendrent un nombre fini (si la trajectoire est périodique, ce qui est rare) ou dénombrablement infini (si elle n'est pas périodique, ce qui est le cas le plus fréquent) de points qui se répartissent le long de la courbe de niveau. Au bilan, la courbe apparaît dense.
L'examen du portrait de phase du billard elliptique révèle la présence de points particuliers, situés respectivement en :
- p=0 et s=0 (ou s=L, ce qui revient au même) et p=0 et s=L/2. Ces points (elliptiques, marqués en vert) correspondent aux extrémités de la trajectoire périodique stable longeant le petit axe de l'ellipse,
- p=0 et s=L/4 ou 3L/4. Ces points (hyperboliques, marqués en rouge) correspondent aux extrémités de la trajectoire périodique instable longeant le grand axe de l'ellipse.
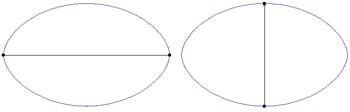
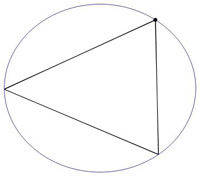
Ces deux trajectoires ont ceci de particulier qu'elle sont isolées : aucune autre trajectoire périodique n'existe qui soit infiniment proche d'elles. C'est la raison pour laquelle son portrait de phase se limite à deux points parfaitement visible sur le portrait global. Le billard elliptique accepte beaucoup d'autres trajectoires périodiques (à plus de deux rebonds), en fait une infinité dénombrable mais elles cessent d'être isolées. Voici, pour l'exemple, quelques trajectoires périodiques triangulaires :
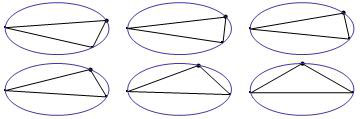
Toutes ces trajectoires résultent d'une déformation continue de l'une quelconque d'entre elles et si le portrait de phase de chacune se limite forcément à 3 points, l'ensemble de ces triplets peuplent densément la courbe de niveau correspondant à leur invariant commun. Ces trajectoires périodiques non isolées sont typique des systèmes intégrables. Nous allons voir que, dans le cas d'un billard non intégrable, les trajectoires périodiques sont généralement isolées et que cela change radicalement l'aspect du portrait de phase.
2. Un billard ovale, non intégrable (chaotique)
On considère le billard dont le contour présente un rayon de courbure égal à :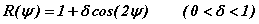
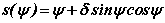
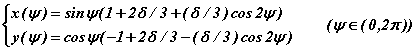
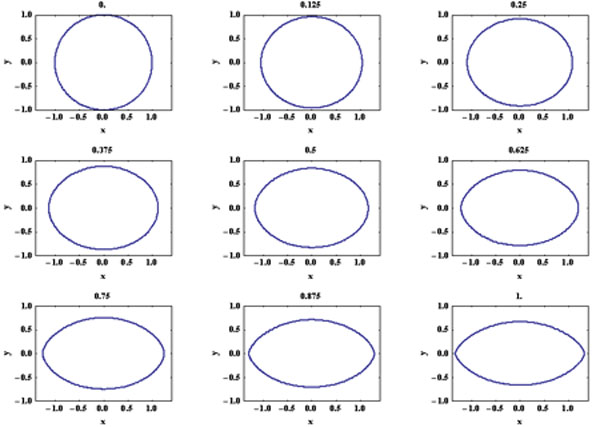
Voici quelques exemples de déformations ovales du cercle primitif (δ=0). Au-delà de δ=1, la frontière cesse d'être simple.
Il n'existe généralement pas d'invariant isolé pour ce type de billard. On s'en rend compte lorsqu'on dresse numériquement le portrait de phase : plus δ se rapproche de 1, plus les points se distribuent irrégulièrement, le signe que les trajectoires adoptent un comportement erratique. Voici une esquisse du portrait de phase dans deux cas opposés, δ=0.2 et δ=0.8
Exemple 1 (peu chaotique) : δ = 0.2.
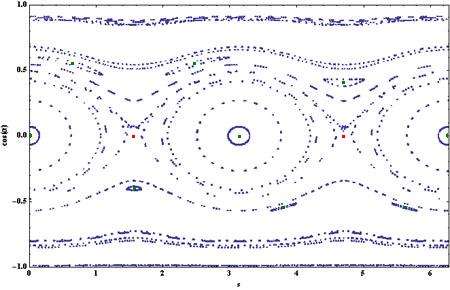
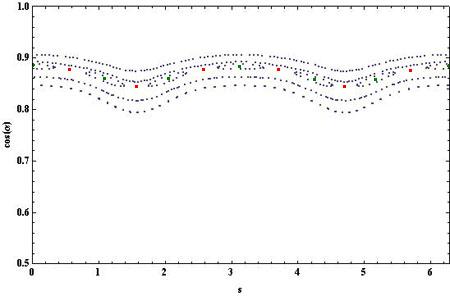
La grande différence avec le billard intégrable elliptique, c'est la présence d'un grand nombre de points fixes elliptiques isolés situés au centre d'îlots de stabilité. Ces points, asssociés par paquets de n, correspondent à une trajectoire périodique isolée à n rebonds. Par exemple, l'ensemble des trois points fixes visibles aux alentours de p=0.5 correspond à une trajectoire triangulaire isolée et l'ensemble des six points fixes visibles sur l'agrandissement correspond à une trajectoire hexagonale isolée :
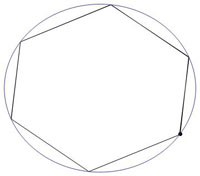
Entre deux points elliptiques, il existe toujours un point hyperbolique (correspondant encore à une trajectoire périodique isolée mais cette fois instable), situé à l'intersection des séparatrices. C'est au niveau de ces points instables que le chaos apparaît en premier lieu lorsque δ croît. Seul un net agrandissement des régions concernées et la prise en considérations d'au moins 10000 trajectoires pourraient mettre le phénomène en évidence lorsque δ ne vaut que 0.2. La situation est plus favorable si δ augmente.
Exemple 2 (nettement chaotique) : δ = 0.8.
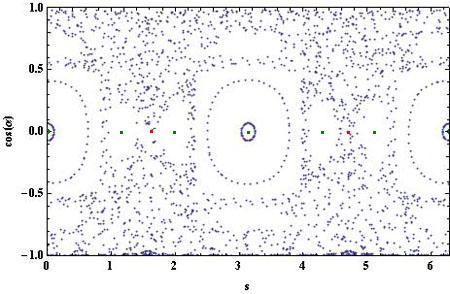
On constate qu'un grand nombre de courbes invariantes ont disparu, remplacée par des point dispersés dans le plus grand désordre. C'est la signature du chaos. Ce chaos prend naissance au niveau des points fixes hyperboliques et le degré de destruction est fixé par le théorème KAM (Kolmogorov-Arnold-Moser). Ce théorème prédit que lorsque l'on perturbe progressivement un système intégrable (ici c'est le paramètre, δ, qui mesure cette perturbation sachant que lorsque δ=0, le billard est circulaire donc intégrable), c'est au voisinage des points hyperboliques que l'invariant garant de la stabilité du système cesse d'exister.
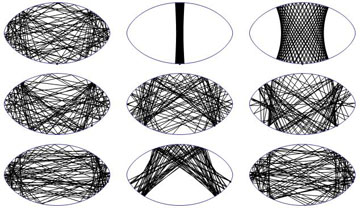
Voici à titre d'exemples 9 trajectoires correspondant aux conditions initiales, ψ0= 0, π/6 et π/3 et α0= 1, 3/2 et 2. On oberve que certaines sont quasi-périodiques et d'autres sont chaotiques :
Variations sur le thème du gaz de Szilard
On précise ici un point abordé par ailleurs, dans un exposé consacré à la Thermodynamique du Calcul. Le gaz parfait de Szilard idéalise une molécule ponctuelle unique, rebondissant perpétuellement et élastiquement sur les parois d'une boîte parallélépipédique à D dimensions (D = 1, 2 ou 3).
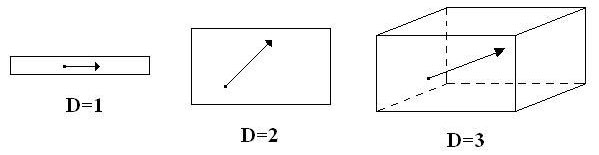
C'est un sujet d'étude classique de calculer les caractéristiques physiques d'un tel gaz et de montrer que les lois du gaz parfait s'appliquent à lui :
-
Equation d'état :
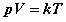
-
Energie interne :
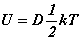
-
Entropie :
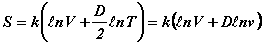
-
Pression :
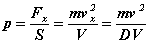
-
Vitesse de la molécule selon la température :
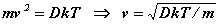
-
Chaleurs massiques :
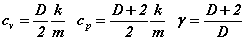
A titre d'exemple, voici le travail extractible du gaz de Szilard monomoléculaire dans quelques cas de figures classiques consistant à ôter ce qu'il faut de masse du contrepoids afin que le volume du gaz double (Dans les cas réversibles *** la masse soulevée l'est par fragments infinitésimaux successifs) :
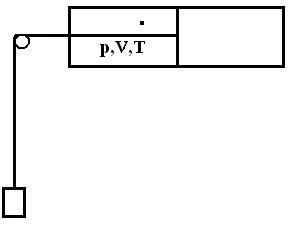
| pf | Vf | Tf | Wextr | ΔS | M | |
|---|---|---|---|---|---|---|
| isoth rév | p/2 | 2V | T | kT ln2 | 0 | *** |
| isoth irrév | p/2 | 2V | T | kT/2 | k(ln2-1/2) | (pV)/(gl) |
| adiab rév | p 2-1-2/D | 2V | 2-2/DT | (1-2-2/D)DkT/2 | 0 | *** |
| adiab irrév | Dp/(2D+2) | 2V | DT/(D+1) | DkT/(2D+2) | k(ln2+(D/2)ln(D/(D+1))) | DpV/((2D+2)gl) |
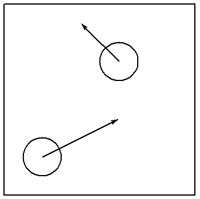
On peut compliquer ce modèle par adjonction de molécules supplémentaires mais cela ne suffit pas à le rendre réaliste. En particulier, cela n'explique pas la croissance de l'entropie jusqu'à l'état d'équilibre. Pour parvenir à cette fin, il faut incorporer un ingrédient indispensable, une dynamique chaotique. On amorce ce processus en considérant deux molécules identiques, assimilées à des disques rigides lancés initialement avec des vitesses quelconques. Un rappel, relatif à la connection entre la thermodynamique et la théorie de l'information s'impose à ce stade. Si l'on considère (dans le cas bidimensionnel, D=2, pour simplifier) un ensemble de N molécules préparées dans un état initial très particulier, soit les positions alignées aux sommets d'une grille régulière et les vitesses identiques, il est clair que l'entropie (au sens de Kolmogorov : longueur, en bits, du plus court programme qui imprime une description complète du système à la précision imposée) de ce gaz hors équilibre est très basse parce qu'il existe un programme très court qui encode son état initial. En réalité, un tel système a vite fait d'évoluer vers un état où les positions se dispersent au hasard de même que les vitesses sauf que celles-ci, demeurant contraintes par la conservation de l'énergie, doivent respecter une loi exponentielle (dite de Boltzmann) de répartition à l'équilibre. Ce sont les chocs intermoléculaires qui sont responsables de cette évolution, encore faut-il qu'ils induisent une dynamique chaotique, seule capable d'allonger le programme d'encodage des positions et des vitesses des molécules donc finalement d'augmenter l'entropie.
Deux molécules assimilées à des disques rigides et élastiques suffisent à développer une dynamique de ce type et ce sont les collisions successives qui sont à la base de la sensibilité requise aux conditions initiales. Il est possible d'écrire un programme qui suit fidèlement l'évolution d'un tel système mais son temps d'exécution est d'autant plus long que le rayon des disques moléculaires est petit en comparaison de la taille de l'enceinte (NB : beaucoup de programmes disponibles dans le commerce prétendent y parvenir en un temps "raisonnable" pour N>>2 mais ils trichent généralement en tronquant la suite complète des événements). La simulation qui suit utilise un grand rayon (R=0.2) pour une enceinte carrée de côté, L=1. Cela augmente le nombre moyen de collisions donc accélère la redistribution des vitesses, sans altérer le pouvoir de suggestion du modèle.
Les conditions initiales des molécules, nommées a et b, sont les suivantes : xa(0)=0.2, ya(0)=0.2, xb(0)=0.6, yb(0)=0.7, vxa(0)=2, vya(0)=1, vxb(0)=-1, vyb(0)=1. Si l'on pose que la masse de chaque molécule vaut 2 dans un système d'unités arbitraires, l'énergie cinétique totale de ce gaz élémentaire vaut 7, répartie initialement, entre a et b, dans le rapport 5/2. Les collisions successives, notoirement chaotiques entre deux disques, vont avoir pour effet de modifier progressivement ce rapport afin qu'il tende vers la parité, aux fluctuations près : c'est l'équiparttion de l'énergie pour laquelle l'entropie est maximale.
Le corps du programme repose sur la loi de transformation des vitesses lors du choc élastique des disques :
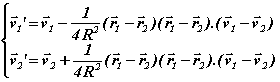
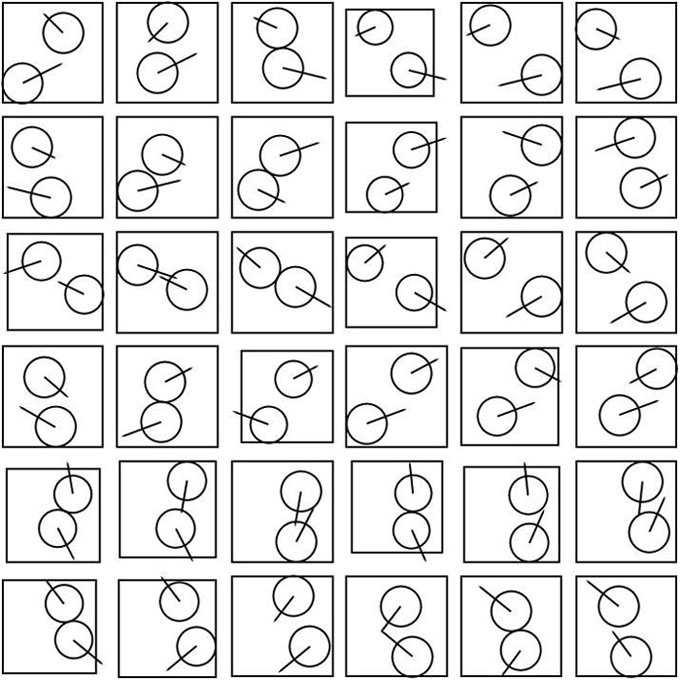
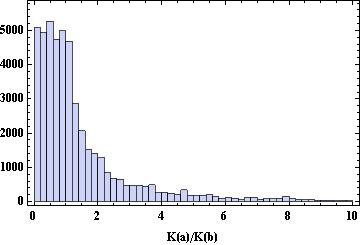
En quasiment 3000 unités de temps, 50000 collisions se produisent dont un peu plus de la moitié sont intermoléculaires (Le programme complet et les détails de calculs sont fournis en annexe (Notebook Mathematica)). C'est largement suffisant pour qu'un équilibre statistique ait le temps de s'installer. L'histogramme du rapport des énergies cinétiques des deux particules, valant initialement K(a)/K(b) = 2.5, se concentre à présent autour de la valeur 1, ce qui correspond à l'équipartition statistique de l'énergie (< Ka> = < Kb> que l'on vérifie par ailleurs, dans l'annexe) donc à l'entropie maximale.
Cette dernière inférence résulte de ce que la composante de l'entropie dépendante des vitesses moléculaires d'un gaz de Szilard bimoléculaire vaut ln(va)+ln(vb)=ln(va vb); son maximum sous la contrainte que va2+vb2 se conserve exige que va=vb.
Remarque finale : on lit fréquemmet que les seules lois de la mécanique newtonienne, notoirement invariantes par renversement du temps, ne peuvent prédire un accroissement irréversible d'entropie. Cela cesse d'être vrai lorsque la dynamique du système est chaotique et que l'on adopte la définition informationnelle (au sens de Kolmogorov) de l'entropie (dans l'unité, k ln(2)), à savoir, la longueur (en bits) du plus court programme qui décrit l'état du système à une précision fixée d'avance. Cette longueur augmente naturellement avec le temps du fait que si on exige une description de l'état actuel précise à 10-n, l'encodage de conditions initiales de plus en plus lointaines exige d'encoder un beaucoup plus grand nombre de chiffres significatifs. Rappelons que l'équilibre du système est atteint lorsqu'aucun programme ne peut prétendre faire mieux que la simple description in extenso : l'entropie cesse alors de croître.
Compressions astronomiques : Hipparque contre Newton
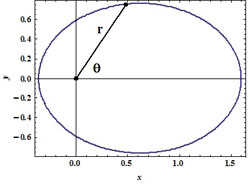
On illustre, sur un exemple simple, ce principe fondamental que la science est l'art de (bien) compresser les données. Le test choisi est certes académique mais il permet de cerner l'enjeu du problème : il s'agit de repérer l'évolution d'un astre autour d'un centre gravitationnel considéré comme fixe, pour simplifier. Nous connaissons, depuis les travaux de Newton, un excellent programme compresseur de l'ensemble des mesures que l'on peut faire à ce sujet. Ce programme encode la résolution des équations hamiltoniennes à partir d'un jeu de conditions initiales (Pour la suite, celles-ci ont été posées égales à, r(0) = 1.6, θ(0)= 0, r'(0) = 0, θ'(0)= 0.3, dans des unités qu'il n'est pas nécessaire de préciser et qui correspondent au choix, μ = 1) :
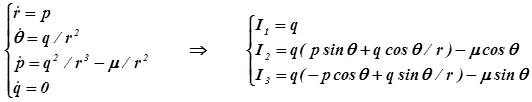
La solution analytique la plus élégante de ce système passe par la recherche des invariants autonomes, moment cinétique (I1) et vecteur de Lenz (I2, I3) (qui incluent la conservation de l'énergie),
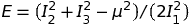
Une simple élimination de p et q entre ces trois invariants autonomes livre la trajectoire elliptique bien connue,
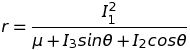
Quant à l'évolution de l'astre le long de cette trajectoire, on la calcule à l'aide du quatrième invariant, nécessairement non autonome (= dépendant explicitement du temps),
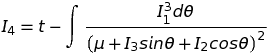
En particulier, voici comment varie l'angle, θ, en fonction du temps sur une période de trajectoire :
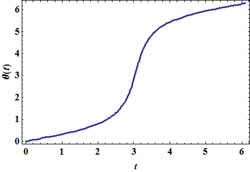
Ce graphe représente l'ensemble des seules mesures accessibles aux premiers astronomes (Les babyloniens, il y a 2700 ans !) qui ont, de fait, commencé à repérer les positions angulaires des planètes par rapport aux étoiles fixes de la voûte céleste.
Hipparque qui vécut entre -190 et -120, fut parmi les premiers à chercher une logique - un programme compresseur - à ces mesures. Convaincu comme le furent beaucoup d'autres encore longtemps après lui que dans un monde parfaitement ordonné par la Divinité, le cercle parfait devait être la clé de toute trajectoire céleste, il s'engagea dans une voie semblable à celle décrite ci-après. Le modèle d'Hipparque sera raffiné trois siècles plus tard par Claude Ptolémée et les choses en resteront là pendant plus de 1000 ans jusqu'à ce que s'installe la révolution copernicienne et les travaux de Kepler et Newton.
Le modèle suivant n'est pas exactement celui d'Hipparque mais il suffit pour illustrer les méfaits d'une compression qui s'engage dans une mauvaise direction. Dans un langage modernisé, nous cherchons une solution modélisée par deux paramètres, a1 et b1, sous la forme trigonométrique,
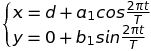
Si on ajuste les valeurs des paramètres libres, a1 et b1, de telle manière que le graphe de θ(t) soit exact en t=2 et t=4, par exemple, les calculs repris en annexe (Notebook Mathematica) révèlent les valeurs, a1 = 0.655882 et b1 = 0.352826. (Note : le paramètre d n'est pas ajustable, en fait, on peut lui donner la valeur que l'on veut car il ne fait que dicter l'échelle dimensionnelle du système. Les mesures angulaires ne contiennent aucune information sur la taile réelle du système gravitationnel étudié, elles ne sont donc pas en mesure de livrer la moindre information à ce sujet et, de fait, les anciens sous-estimaient largement la taille du système solaire).
On contrôle la validité de ce modèle approximatif en superposant les courbes exacte et approchée, puis en affichant la différence absolue entre les deux :
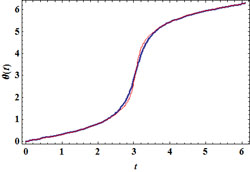
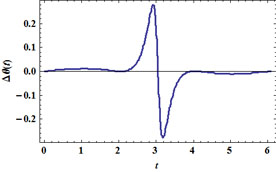
La trajectoire complète est une ellipse mais ce n'est pas la "bonne" ellipse newtonienne. Elle n'est pas davantage parcourue à la "bonne" vitesse mais au bilan les erreurs se compensent presque exactement donnant l'illusion d'un modèle valable.
On peut géométriser ce modèle en faisant appel à deux cercles générateurs, cela fera plaisir à Hipparque. Observez que le cercle rouge est parcouru à vitesse constante dans le sens trigonométrique et que le cercle vert est parcouru à la même vitesse constante mais dans le sens inverse) : au bilan, le point vert qui représente l'astre en mouvement décrit la trajectoire annoncée.
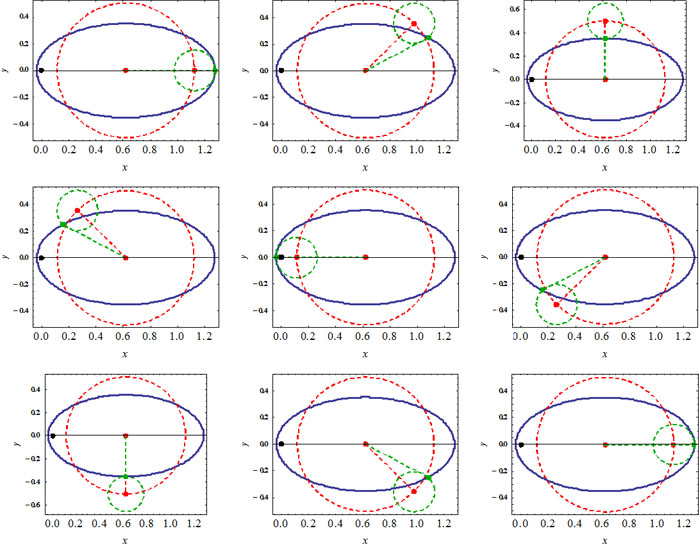
Vu que le modèle précédent ne compresse qu'imparfaitement les données, l'idée vient naturellement de le raffiner en introduisant deux paramètres supplémentaires, a2 et b2, et de recommencer l'ajustement sur base du modèle affiné,
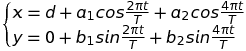
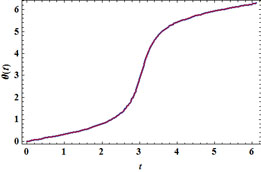
Cette fois, on peut exiger que le graphe de θ(t) soit exact en quatre points, t = 2, 2.5, 3.5 et 4 (par exemple) : les calculs repris en annexe trouvent les valeurs, a1 = 0.788279, a2 = 0.153621, b1 = 0.269198 et b2 = 0.0896554. On contrôle comme suit l'amélioration apportée par ce modèle raffiné :
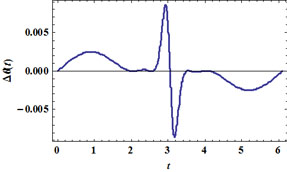
La géométrisation fait cette fois appel à quatre cercles générateurs : le cercle rouge est parcouru à vitesse constante dans le sens trigonométrique, le cercle vert est parcouru à la même vitesse constante mais dans le sens inverse, le cercle violet en sens direct à vitesse double et le cercle noir, à vitesse double et en sens inverse. Au bilan, le point noir qui représente l'astre en mouvement décrit une trajectoire excessivement excentrée qui n'est plus elliptique.
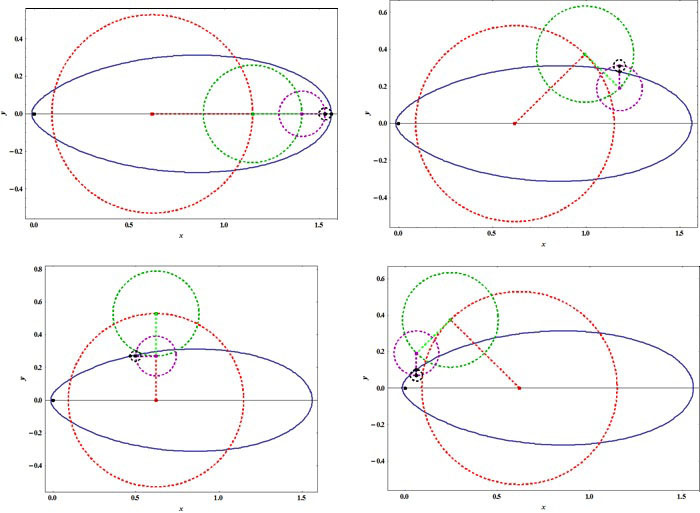
Il semblerait qu'on puisse se montrer très satisfait du résultat obtenu : quelques lignes de programme, à peine, garantissent une précision d'au moins un pour mille. A priori, cela semble nettement plus compact que le programme de Newton qui doit naturellement contenir toutes les sous-routines qu'impliquent la résolution numérique des équations différentielles hamiltoniennes. Le modèle newtonien est pourtant supérieur à deux égards :
- il ne se contente pas de compresser la donnée angulaire, θ(t), il fait de même avec les distances mesurées ce que ne fait pas le modèle d'Hipparque. Il suffit pour s'en convaincre de comparer les trajectoires issues des deux modèles, seule l'ellipse newtonienne correspond à la réalité.
- le critère de la taille du programme compresseur est certes essentiel mais il faut également veiller à l'augmentation de la taille de ce programme lorsqu'une précision accrue est exigée. C'est là que le modèle newtonien prend toute sa valeur : pour obtenir une précision double, le modèle newtonien n'exige que l'encodage des conditions initiales en précision double. En comparaison, la série trigonométrique d'Hipparque converge tellement lentement qu'elle nécessite l'adjonction de termes supplémentaires de plus en plus nombreux au point que la dimension du programme compresseur finit par exploser.
Chorégraphies classiques
En mécanique newtonienne, on nomme chorégraphie le ballet que N corps (N>2) décrivent dans l'espace à trois dimensions, sous l'effet des forces de gravitation, pourvu que les trajectoires soient périodiques dans le temps. Un article paru récemment (M. Šuvakov and V. Dmitrašinović, Three Classes of Newtonian Three-Body Planar Periodic Orbits, Phys. Rev. Lett. 110, 114301 (2013), arXiv:1303.0181) fait état de nouvelles découvertes de ce genre dans le cas de 3 masses égales évoluant dans un plan. Les résultats esthétiques font l'objet d'une présentation particulièrement réussie sur ce site.
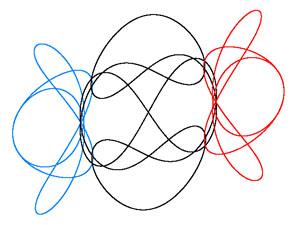
On y apprend qu'une configuration en forme de papillon est possible pour trois masses unitaires sous réserve de respecter un jeu précis de conditions initiales : positions initiales en (-1, 0), (0, 0) et (+1, 0) et vitesses initiales valant respectivement, (v1, v2), (-2 v1, -2 v2) et (v1, v2), où v1 = 0.306893 et v2 = 0.125507. Une trajectoire complète est balayée en 6.235641 unités de temps. Dans les figures proposées, 3 couleurs différentes ont été utilisées pour distinguer les trajectoires.
La figure précédente, empruntée à l'article original, n'est pas dessinée à l'échelle. On a comblé cette lacune en recalculant l'évolution du système en annexe (Notebook Mathematica).

On rend les trajectoires plus lisibles en les restreignant aux deux premières unités de temps d'où on distingue clairement les points de départ et le début de l'évolution de chacune :

Un point demeure cependant obscur, qui concerne les conditions physiques autorisant ce type de mouvement. Les calculs précédents ont, en effet, été effectués dans un système d'unités réduites sans rapport avec les étalons habituels, le kilogramme, le mètre et la seconde. Il est instructif de repasser aux unités internationales afin de mieux visualiser les bornes des trajectoires et accessoirement de s'assurer que les vitesses ne s'approchent pas de celle de la lumière, auquel cas les équations de Newton perdraient toute signification.
Dans le système international, le hamiltonien qui caractérise entièrement le système à 3 corps, s'écrit en toute généralité :
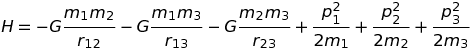
En fait, les calculs ont été effectués sur base d'un hamiltonien réduit, où la constante de la gravitation, G, a été posée égale à 1. Cela présuppose que l'on a défini de nouvelles unités de masse, de longueur et de temps, M, R et T, permettant de réécrire H sous une forme pure (sans unité), où les lettres grecques désignent les grandeurs physiques également débarrassées de leur unité naturelle :
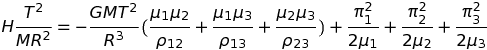
Passer de la valeur classique pour la constante universelle de la gravitation, G = 6.6723 10-11 m3/(s2kg), à la valeur pure, G = 1, revient à substituer au kilogramme, au mètre et à la seconde des unités, M, R et T satisfaisant la relation,
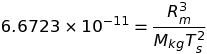
Il y a donc une triple infinité de conditions initiales garantissant des trajectoires en forme de papillon, de dimensions évidemment différentes. Le dernier paragraphe illustre ce point sur deux exemples aux échelles dimensionnelles opposées.
- L'exemple 1 est académique : M = 1 (kg) et L = 1 (m), autrement dit 3 masses d'un kg sont initialement alignées à 1 mètre de distance l'une de l'autre, quelque part dans l'espace, loin de toute autreinfluence gravifique. Pour déterminer les vitesses initiales qu'il convient de leur communiquer, il faut connaître l'unité de temps, T. La relation précédente fournit la valeur, T = 122423 (s) = 1.41693 (jours). Vu que l'unité de longueur n'a pas changé (L = 1 (m)), les vitesses pures, v1 = 0.306893 et v2 = 0.125507, doivent simplement être multipliées par 1/T, ce qui donne : v1 = 2.50682 10-6 et 1.02519 10-6 (m/s). Ces valeurs sont très faibles d'où la période du mouvement est longue, soit, 6.324449 x 122423 (s) = 774258 (s) = 8.96132 (jours).
- L'exemple 2 est plus proche d'une réalité astronomique : M = 1022 (kg) et L = 108 (m). Pour déterminer les vitesses initiales, il faut recalculer l'unité de temps, T. La même relation fournit une valeur 10 fois plus grande qu'au point 1 alors que L est 100 millions de fois plus grand. Il en résulte que les vitesses, v1 = 0.306893 et v2 = 0.125507, multipliées par L/T, sont 107 fois plus grandes, soit, v1 = 25.0682 et 10.2519 (m/s). La période du mouvement est naturellement 10 fois plus grande, soit, 89.6132 (jours).
Dans tous les cas étudiés, les vitesses demeurent faibles par rapport à celle de la lumière (c = 3 108 (m/s)) et l'approximation newtonienne classique est valable. Cela cesserait d'être vrai si les masses augmentaient considérablement plus vite que les dimensions des systèmes astronomiques. A ma connaissance, personne n'a jamais calculé une chorégraphie relativiste.
Chute libre relativiste
On considère le cas (idéalisé) d'un point matériel de masse (au repos), m0, initialement au repos (v0 = 0), tombant d'une altitude, r0, sur un centre de masse, M. On pose M>>>m0 afin d'être en mesure de considérer que ce centre demeure fixe. En mécanique classique, l'équation de Newton, F = - GMm0/r2 = d(m0 v)/dt, décrit cette chute et il n'y a pas besoin de mettre des vecteurs, vu qu'on est à une dimension.
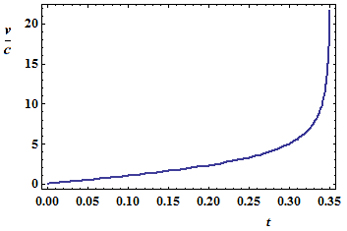
A mesure que le point chute, r tend vers 0, la force tend vers l'infini donc ausi l'accélération et la vitesse. La conservation de l'énergie confirme ce dernier point :
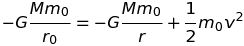
La solution qui précède n'est réaliste qu'aux faibles vitesses, v/c << 1 : on sait, depuis Einstein, que la vitesse d'un point matériel ne peut excéder, c, la vitesse de la lumière. En fait l'équation de Newton cesse d'être valable lorsque v approche c.
Physiquement, on peut voir les choses comme suit : lorsqu'un objet prend de la vitesse, sa masse inerte incorpore l'énergie cinétique acquise, K, sous la forme d'un complément de masse Δm = K/c2. L'équation de mouvement s'écrit encore, F = - GMm/r2 = d(m v)/dt, où y a lieu de remplacer la masse au repos, m0, par la "masse en mouvement", m = m0/sqrt[1-v 2/c 2]. L'équation complète s'écrit à présent :
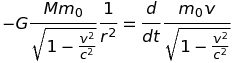
Le second membre de cette équation incorpore le fait que la masse inerte du point matériel augmente au-delà de toute limite lorsque v approche c, rendant toute accélération additionnelle de plus en plus difficile. Toutefois, le premier membre nous apprend que la force de gravitation augmente, elle aussi, au-delà de toute limite, précisément parce que la masse du point ne cesse d'augmenter. Ces deux effets agissent clairement en sens contraire et il n'est pas clair a priori qui l'emporte. En fait les calculs numériques repris en annexe (Notebook Mathematica) montrent que le second membre dicte sa loi au premier, interdisant à la vitesse de dépasser la limite, c. On peut les confirmer analytiquement en observant que l'équation de mouvement peut être réécrite et intégrée sous la forme :
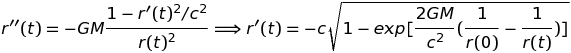
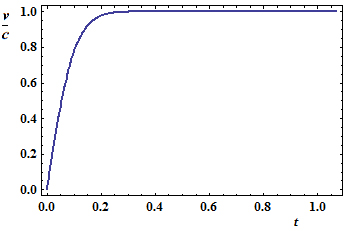
On voit que v = r'(t) tend effectivement vers -c à mesure que r se rapproche de 0 (le signe - parce que l'axe des vitesse pointe vers l'infini). Cette solution peut encore s'écrire sous la forme d'une intégrale première (= constante du mouvement) :
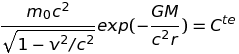
Sa forme est inhabituelle car la force relativiste dépendant de la vitesse, elle ne dérive pas d'un potentiel au sens ordinaire du terme.
Ce calcul a été effectué dans le cadre de la théorie de la Relativité restreinte. A ce titre, il considère que le mouvement se déroule dans un espace euclidien, muni d'une métrique Minkowskienne prenant en compte l'invariance de c pour tous les observateurs inertiels. On considère, depuis 1916 (date de la publication de la théorie de la Relativité générale), qu'une théorie plus correcte de la gravitation doit prendre en considération une métrique plus compliquée correspondant à un espace (non euclidien) déformé par le centre attracteur. Il y aurait lieu de reprendre les calculs, dans cette perspective, pour un résultat similaire : la vitesse de la lumière reste invariante (en grandeur pas en direction) pour tous les observateurs, inertiels ou non, et elle demeure une limite infranchisable. Dans tous les cas, l'existence d'une limite de vitesse infranchissable est liée au fait que pour la dépasser il faudrait dépenser une énergie infinie ce qui n'est pas possible. A noter qu'en Relativité générale, le problème de la chute se complique du fait de l'existence, à proximité immédiate du centre, d'une singularité liée à l'horizon de Schwarzschild, RS = 2G M/c2 (Effet de trou noir).
Il est également possible de développer un argument logique prouvant que c est infranchissable. On montre en relativité qu'un observateur qui dépasserait cette limite serait capable d'inverser l'ordre temporel entre deux événements dont l'un serait la cause naturelle de l'autre. Une telle rétroaction dans le temps serait perçue comme une violation du principe de causalité qui interdit communément à l'effet de précéder sa cause sous peine de paradoxes insurmontables.
Attraction universelle
On sait, depuis Newton, que tous les corps massifs s'attirent en raison directe du produit de leurs masses et en raison inverse du carré de la distance qui les sépare, soit : F = G M1M2/r2. G est une constante universelle dont la valeur est, G = 6.67 10-11 m3/(kg s2), dans le système international d'unités. Cette loi ne suffit pas, il manque le mode d'emploi, également fourni par Newton : dans un référentiel inertiel (cfr l'article 15 pour une définition), tout corps de masse, m, qui subit une force extérieure, F, prend une accélération, a = F/m. Ces deux lois suffisent à décrire à peu près exactement le comportement des objets massifs usuels. Un écart subsiste cependant, minuscule dans le cas des planètes du système solaire (c'est Mercure qui en souffre le plus) mais plus important dans le cas d'objets super-massifs (Trous noirs, par exemple). C'est la Relativité Générale qui explique le mieux (actuellement !) cet écart : Einstein ne croit pas à la notion de force, d'ailleurs il n'en a pas besoin. Il postule plutôt que toute masse, M, courbe l'espace-temps voisin selon une loi bien définie, au point qu'il cesse d'être euclidien. A nouveau, cette loi ne suffit pas, il manque le mode d'emploi : toute masse extérieure, m, qui s'approche de M suit une trajectoire (dite géodésique) qui extrémise le temps propre écoulé, celui mesuré par l'horloge qui accompagne m. Cette horloge doit être synchronisée, à tout instant, dans le référentiel inertiel tangent, en respectant la procédure issue de la Relativité restreinte et basée sur l'invariance de la vitesse de la lumière, c.
Revenons au cas simple, newtonien : Deux billes de verre sphériques identiques, de rayon R et de masse m, sont initialement immmobiles à la distance mutuelle, r0, mesurée de centre à centre. Elles déforment donc l'espace-temps et les lois d'Einstein devraient permettre d'établir qu'elles vont se rapprocher jusqu'à se toucher. Combien de temps cela prendra-t-il ? En fait, il n'est pas nécessaire de déployer l'artillerie lourde pour résoudre ce problème, les lois de Newton suffisent amplement car les masses concernées sont bien trop faibles pour que la relativité introduise une correction ! Le mouvement s'effectuant à une seule dimension (l'axe joignant les centres des billes), il suffit d'écrire que l'énergie se conserve sous la forme (v = dr/dt) :
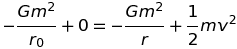
On trouve la distance ρ (de centre à centre) à tout instant, τ, en intégrant :
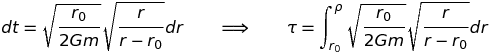
Le résultat s'écrit :
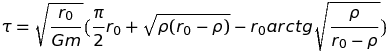
Exemple numérique : si on pose que le rayon des billes vaut, R = 1 cm, que leur densité est égale à 2.5 et que la distance de départ vaut r0 = 1m, on trouve que le temps qu'il faut pour qu'il y ait contact, soit ρ = 2R, vaut 21.7 jours. On note que ce temps s'allonge indéfiniment lorsque m tend vers 0, ce qui est raisonnable.
Galilée versus Lorentz
La notion d'observateur est essentielle en physique, particulièrement lorsqu'il est inertiel. Par définition, un observateur est globalement inertiel lorsqu'il dérive librement (= sans frein ni moteur) dans un espace suffisamment vide de matière et sans rotation par rapport aux étoiles lointaines. Les observateurs globalement inertiels sont privilégiés : ils écrivent les lois de la physique plus simplement que n'importe quel autre observateur. Strictement parlant, de tels observateurs n'existent pas car dans toute portion de l'espace où l'on se propose de faire de la physique intéressante, il y a généralement au moins un astre plus ou moins proche. Cependant les observateurs terrestres ne sont pas si éloignés que cela de cet idéal et ils ont appris à faire les corrections nécessaires en fonction de la précision exigée pour l'analyse des résultats de leurs expériences.
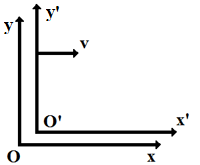
Tout observateur, O', en translation rectiligne uniforme (MRU) par rapport à un observateur globalement inertiel, O, est également globalement inertiel et on passe des coordonnées de l'un à celles de l'autre par la transformation de Galilée, dans le cas classique (typiquement aux faibles vitesse, v<<c), et de Lorentz dans le cas relativiste. Dans un système d'unité où la vitesse de la lumière vaut, c = 1, la vitesse relative entre les observateurs, v, est une nombre compris entre 0 et 1. On pose pour simplifier que cette vitesse relative est alignée selon les axes x et x' confondus. Avec ce choix d'unités, les coordonnées x et t se mesurent en mètres. Les transformations de coordonnées se notent:
- Galilée : x' = x - v t et t' = t qui s'inversent en x = x' + v t' et t = t',
- Lorentz : x' = γ (x - v t) et t' = γ (t - v x) qui s'inversent en x = γ (x' + v t') et t = γ (t' + v x') (on a posé, γ = (1-v2)-1/2).
C'est un sujet d'étude classique de déduire que l'espace et le temps sont absolus dans le premier cas et relatif dans le second. Plus précisément, étant donné un intervalle de temps et une distance, mesurés dans le référentiel au repos, il s'agit d'établir ce que mesure un observateur en mouvement. Le protocole suivant doit être respecté si l'on veut que ces comparaisons aient un sens :
- Dans le référentiel au repos, il importe que l'intervalle de temps considéré sépare deux événements se produisant au même endroit (Δx = 0), sans quoi on pourrait craindre un retard temporel parasite dû au fait que l'information ait mis des temps différents pour parvenir à l'observateur (L'information ne se propage pas à vitesse infine mais à vitesse, c).
- Le repérage des abscisses des extrémités du segment que l'on veut mesurer peut se faire à n'importe quel instant dans le référentiel eu repos (Δt quelconque) mais pas dans le référentiel en mouvement : on doit impérativement avoir Δt' = 0 car il n'y aurait aucun sens de repérer, à des instants différents, les extrémités d'un segment mobile que l'on veut mesurer.
Le calcul est trivial dans le cas classique, on a successivement : Δt = Δt' et Δx = Δx' + v Δt' = Δx', autrement dit les deux observateurs mesurent les mêmes intervalles de temps et d'espace.
Il est moins immédiat dans le cas relativiste et le respect des deux contraintes mentionnées (Δx = 0 et Δt' = 0) livre sans trop de peine, Δt' = γ Δt - v γ Δx = γ Δt (dilatation du temps) et Δx' = γ Δx - v γ Δt = γ Δx - γ v2 Δx = Δx/γ (contraction des longueurs). Ces relations concernent l'observateur O' en translation uniforme par rapport à O. Naturellement, dans le cas où O' se considère au repos, c'est O qui est en mouvement à la vitesse -v et les formules précédentes deviennent, Δt = γ Δt' et Δx = Δx'/γ. Il n'y a pas contradiction entre les deux groupes de formules car elles concernent des observateurs différents.
Il est intéressant de traduire les transformations de Galilée et de Lorentz en forme graphique et de retrouver les formules de contraction et de dilatation.
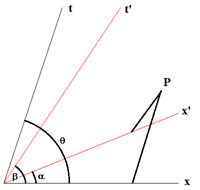
Ces lois de transformation rappellent, en effet, formellement les formules de changement d'axes en géométrie analytique du plan (x, t). L'analogie n'est cependant parfaite que moyennant quelques précautions qui ne sautent pas aux yeux. On rappelle que les relations de changement de repères (obliques) se notent en toute généralité :
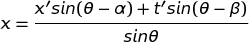
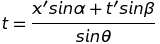
On peut poser θ = π/2 sans altérer la généralité de l'étude. Cela a pour effet de rendre orthogonaux les axes, x et t, de l'observateur O présumé immobile. Par contre, les axes x' et t' doivent demeurer obliques. Les projections se font parallèlement aux axes comme indiqué sur la figure ci-contre, dans le cas du point P. Avec ce choix, θ = π/2, les formules de changement d'axes se simplifient en :
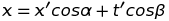
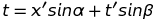
Aucun choix d'angles α et β ne permet de réduire ces formules aux transformations en vue (Galilée et Lorentz). Pour que cela soit possible, il faut adopter des échelles différentes dans la représentation graphique des coordonnées x' et t'. Cela revient à introduire des facteurs d'échelle, λ et μ :
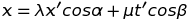
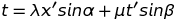
Etudions en détails le cas de la transformation de Lorentz, on doit avoir :
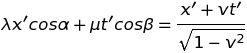
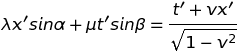
Il suffit d'identifier les coefficients des variables, x' et t', pour trouver l'orientation correcte des axes et les facteurs d'échelle. On trouve : λ = μ = (1+v2)1/2/(1-v2)1/2, tg(α) = v et tg(β) = 1/v (Les angles α et β sont complémentaires).
Les calculs sont plus simples dans le cas de la transformation de Galilée et on trouve cette fois : λ = 1, μ = (1+v2)1/2, α = 0 et tg(β) = 1/v. Les figures qui suivent résument les situations. Insistons sur le fait que les unités portées sur les axes issus de O et de O' s'expriment bien en mètres dans tous les cas et que ce sont les représentations géométriques de ces unités qui sont affichées avec des échelles différentes. Tout calcul effectué sur base de ces figures doit en tenir compte.
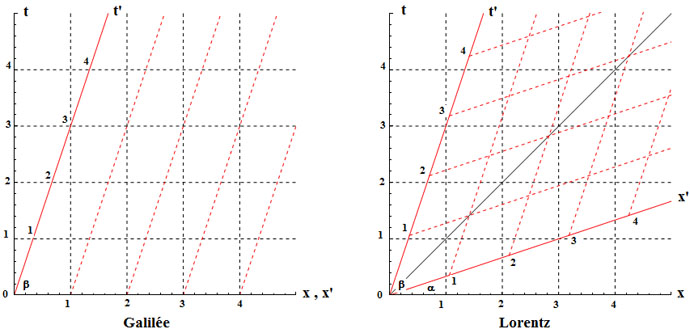
Commençons par expédier le cas peu intéressant de la transformation de Galilée. La figure (de gauche) est exagérée puisque la vitesse est sensée être très inférieure à c (L'axe t' devrait quasiment coïncider avec l'axe t). Quoi qu'il en soit, on voit qu'une longueur unité pour O (base des parallélogrammes) est vue à l'identique (à t' constant) par O', soit Δx = Δx'. En ce qui concerne l'intervalle de temps unité, mesuré par O, il semblerait à première vue qu'il est vu plus grand par O' (Hypoténuse du triangle rectangle lié à l'origine, valant (1+v2)1/2) mais c'est une illusion que corrige le facteur d'échelle, μ = (1+v2)1/2. Lorsqu'on tient compte de ce facteur, on trouve que l'intervalle de temps est identique pour O et O', soit Δt = Δt'. Envisageons, à présent, le cas relativiste, plus intéressant mais plus délicat.
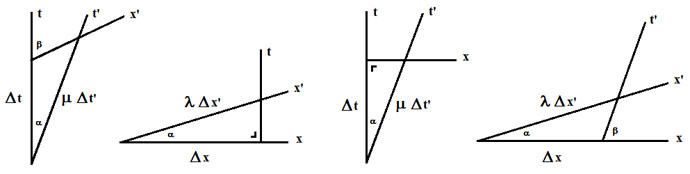
La dilatation du temps et la contraction des longueurs résultent de l'application de la relation des sinus dans les triangles représentés ci-contre.
Les deux figures de gauche considèrent que l'observateur O' est immobile et que O est en mouvement. Imposant les contraintes, on trouve, dans l'ordre :
- Δx = 0 (on a bien que les extrémités de Δt se situent à x constant) d'où, par résolution du triangle, Δt' = γ Δt, et
- Δt' = 0 (les extrémités de Δx' sont repérées à t' constant) d'où, par résolution du triangle, Δx' = Δx/γ.
Les deux figures de droite considèrent que l'observateur O est immobile et que O' est en mouvement. Imposant les contraintes, on trouve, dans l'ordre :
- Δx' = 0 (on a bien que les extrémités de Δt' se situent à x' constant) d'où, par résolution du triangle, Δt = γ Δt', et
- Δt = 0 (les extrémités de Δx sont repérées à t constant) d'où, par résolution du triangle, Δx = Δx'/γ.
Dans tous les cas la prise en compte des facteurs d'échelle, λ = μ = (1+v2)1/2/(1-v2)1/2, est essentielle.
Le faux paradoxe des vrais jumeaux
Cette histoire n'a jamais vraiment cessé de faire couler de l'encre. Bien entendu aucun paradoxe ne pouvant exister dans une théorie physique consistante, ce problème est, de fait, résolu depuis longtemps. Sinon il y a longtemps qu'on aurait changé la théorie et cela se saurait. En substance, le "paradoxe" fait référence à deux jumeaux qui se quittent temporairement pour un voyage relatif. Chaque jumeau, qui connait la théorie de la Relativité restreinte, voit son frère se déplacer par rapport à lui et s'attend à le retrouver plus jeune au moment du retour. Si cela devait se confirmer, la théorie serait inconsistante.
Cette analyse repose sur le fait bien connu que lorsqu'un observateur (globalement) inertiel mesure (avec ses propres instruments) un intervalle de temps vécu par un autre observateur inertiel, en translation rectiligne uniforme à la vitesse, v, par rapport à lui, il trouve un temps dilaté. Cet intervalle de temps pouvant correspondre à un certain nombre de battements de coeur, il en résulte que le jumeau au repos s'attend à ce que son frère vieillisse moins vite que lui.
Elle ignore cependant le fait essentiel que les jumeaux ne peuvent prétendre demeurer inertiels pendant toute la durée de l'expérience : si l'on pose pour simplifier que le jumeau au repos n'a pas cessé de l'être, son frère qui a voyagé a nécessairement dû interrompre sa translation uniforme ne serait-ce que pour faire demi-tour et venir se comparer physiquement à son jumeau. En inversant le sens de sa vitesse, ce frère voyageur a cessé d'être inertiel, ce qui rompt la possibilité d'un raisonnement symétrique. Voyons cela quantitativement en posant, pour simplifier, qu'au départ les deux frères sont au repos dans un même référentiel inertiel. Pour fixer les idées, appelons les frères Félix (F pour fixe) et Marcel (M pour mobile). Le jour de leur 21ème anniversaire, ils se mettent d'accord sur le protocole suivant : F demeure fixe dans le référentiel initial et M entame un périple devant durer, τ = 7 ans, pour l'aller et, τ = 7 ans, pour le retour, soit au total, 2τ = 14 ans, temps mesuré à l'aide de l'horloge embarquée par M. La trajectoire de M dans l'espace-temps de F est connue des deux jumeaux : elle se compose de deux translations à vitesses, v, et ,-v, séparées par un demi-tour supposé instantané.
Pour F, les choses sont simples car étant globalement inertiel, il peut utiliser les lois de la relativité restreinte. Dans son référentiel, F sait que sa trajectoire d'espace-temps correspond au temps propre maximum. Autrement dit, quel que soit le mouvement adopté par M, F sait qu'au moment du retour à la maison, M paraîtra plus jeune que lui, conformément à l'inégalité suivante (On pardonnera l'utilisation du mot anglais pour désigner le vieillisement, trop long en français) :
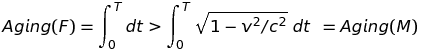
Dans l'exemple qui nous intéresse le calcul des intégrales est immédiat puisque les intégrands sont constants. Les calculs numériques sont simples et parlants si l'on pose que la vitesse relative est proche de la vitesse de la lumière, soit : v = 24/25 c (Valeur empruntée à Taylor et Wheeler - Space Time Physics). Le facteur de Lorentz vaut simplement : (1 - v2/c2)1/2 = 7/25.
On pourrait s'inquiéter de ce que ce modèle ne tient pas compte de l'accélération initiale de M (lorsqu'il quitte F) et de la décélération finale (lors du retour) mais ce point n'est pas essentiel car on peut imaginer un protocole modifié où ces accélérations n'existent pas, les deux frères se faisant signe lorsqu'ils passent l'un en face de l'autre, par deux fois (au départ et à l'arrivée), tout en brandissant une pancarte qui affiche à tout instant l'âge mesuré par chacun.
Le vieillissement de M, mesuré par lui, vaut 2τ = 14 années, par hypothèse. On écrit donc : Aging(M) = 2τ = 14 = T (1 - v2/c2)1/2 = 7T/25, d'où T = Aging(F) = 50 années. Pour F, tout est clair : au moment des retrouvailles, il s'attend à être âgé de 21 + 50 = 71 ans alors que son frère n'aura que 21 + 14 = 35 ans. Toute autre trajectoire, plus compliquée, empruntée par M (et respectant les 14 années de temps propre à M) ne changerait évidemment rien à l'âge final de M (35 ans) mais modifierait celui de F.
F peut raisonner autrement, sur base de l'effet Doppler relativiste longitudinal : imposons à l'horloge de M d'émettre un flash lumineux, en direction de F, toutes les secondes et voyons à quel rythme F les reçoit (On peut remplacer les tics de l'horloge par les battements du coeur de M !). Lors du mouvement d'éloignement il les reçoit à un rythme ralenti, (1 - v/c)1/2 / (1 + v/c)1/2 = 1/7, mais c'est le contraire lors du retour, (1 + v/c)1/2 / (1 - v/c)1/2 = 7. Au bilan, tout se passe comme si F appréciait très différemment les durées de chaque trajet (un rapport 49 dans l'exemple). On a bien : τ (1 - v/c)1/2 / (1 + v/c)1/2 + τ (1 + v/c)1/2 / (1 - v/c)1/2 = 2τ / (1 - v2/c2)1/2 = 50 ans.
Il est intéressant mais nettement plus délicat de raisonner du point de vue de M. La difficulté provient du fait que M ne peut plus appliquer les lois de la relativité restreinte à tout instant car il cesse d'être inertiel lors de la phase d'inversion du mouvement.
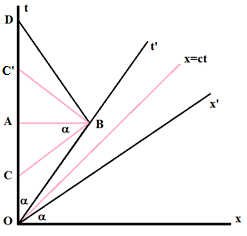
Du point de vue de M, il est bien vrai que chaque MRU a pour conséquence un ralentissement du vieillissement de F d'un facteur 7/25. Sur cette seule base, M prédirait pour F un vieillissement de 14 (7/25) = 3.92 années seulement ce qui contredirait fortement le résutat précédent (50 ans pour rappel !). Ce calcul est cependant largement incomplet car il ne tient pas compte de la phase d'inversion des vitesses. Pour y voir plus clair, considérons d'abord le diagramme ci-contre qui représente le voyage, OBD, de M, dans les référentiels liés à F (x et t) et à M (x' et t'). Par hypothèse, le voyage aller dure 7 ans, mesurés par M : sur la figure, le segment correspondant, OB (aligné sur l'axe t'), mesure 7λ = 12011/2 (n'oubliez pas le facteur d'échelle, λ = (1+v2/c2)1/2/(1-v2/c2)1/2 = 12011/2/7, cfr article 15). Sachant que tg(α) = v/c = 24/25, d'où cos(α) = (1+v2/c2)-1/2 = 25/12011/2 et sin(α) = (v/c) (1+v2/c2)-1/2 = 24/12011/2, on dispose de tout ce qu'il faut pour calculer les segments OC et CA (donc leurs symétriques, C'D et AC'), tous alignés sur l'axe t : il suffit d'appliquer la relation des sinus aux triangles OCB et CAB. On trouve : OC = C'D = 49/25 = 1.96 et CA = AC' = 242/25 = 23.04, d'où OA = 25 et OD = 50 années comme attendu. Les segments, CB, et son symétrique, BC', représentent les lignes de simultanéité pour M (t' y est constant, d'abord à l'aller puis au retour, axes x' et t' non représentés dans ce deuxième cas pour ne pas encombrer la figure). Autrement dit, du point de vue de M, le vieillissement de F calculé sans tenir compte de l'inversion de trajectoire correspond aux seuls segments OC+C'D = 3.92 années. Les segments manquants, CA+AC' = 46.08 années, comptabilisent les effets de l'accélération brutale subie par M.
Il reste à comprendre l'origine physique de la désynchronisation de l'horloge de F telle que perçue par M au moment de l'inversion de trajectoire (le segment CC' = 46.08 années, aligné sur t). Lors de cette inversion, M, qui se considère au repos, ressent un violent pseudo-champ de pesanteur orienté dans le sens opposé à l'accélération relative, g, entre M et F, donc dans le sens allant de F vers M. Tout se passe, pour M, comme si F et M se situaient pendant un court instant en deux points, situés à distance d, entre lesquels règnent une différence de potentiel gravifique considérable valant, φ = g d. On sait que l'horloge située au point de potentiel le plus bas accélère par rapport à l'autre d'un facteur φ/c2. Lors du demi-tour, M, passe brutalement, disons plutôt en un temps très court, Δt', de la vitesse v à la vitesse -v : il éprouve un pseudo-champ de gravitation, φ = 2v d /Δt'. M se situe en amont dans ce champ, là où le potentiel gravifique est plus élevé, et F se situe en aval, où le potentiel est plus bas, et d est la distance séparant M de F. Pour F, cette distance, d, vaut AB = v T/2 (24 années dans l'exemple si on pose c=1) mais pour M, qui nous intéresse plus particulièrement, elle ne vaut que, d = v T/2 (1 - v2/c2)1/2 (contraction de Lorentz). Pendant le très court intervalle de temps qu'a duré l'inversion de vitesse, la marche, Δt, de l'horloge de F est vue, par M, considérablement accélérée, du facteur, φ/c2. Autrement dit, M voit Δt durer (1 + φ/c2)Δt, soit un accroissement de 2v d (Δt/Δt')/c2. Dans l'exemple, en tenant compte de la dilatation des temps mesurés par F et M , Δt/Δt' = 1/(1 - v2/c2)1/2 , on (re)trouve que, pour M, l'horloge de F avance brutalement d'une quantité égale à : (2v/c2)(vT/2) = (24/25)2 50 = 46.08 années, c'est bien la mesure du segment CC' qu'on voulait expliquer. En résumé, au cours de son voyage, M a vu l'horloge de F tourner plus lentement la majeure partie du temps mais galoper à folle allure pendant le court instant qu'a duré l'inversion de vitesse, ce dernier effet l'emportant largement, au bilan.
Cette analyse est grossière dans la mesure où, dans la réalité, le demi-tour exécuté par M ne peut se faire instantanément. Il y aurait lieu de reprendre les calculs sur des bases plus réalistes en posant par exemple que M suit une trajectoire qui l'éloigne de F puis le rapproche continûment. La prédiction de l'âge de M, effectuée par F, demeurerait facile, elle serait encore donnée par l'intégrale ci-dessus. Par contre la prédiction de l'âge de F, effectuée par M, devrait tenir compte du pseudo-champ de gravitation vécu par M, à tout instant, ce qui nécessiterait de connaître la métrique d'espace-temps correspondant à la trajectoire suivie.
Optique quantique, un bel exemple de pléonasme
Les lois, quantiques, qui régissent le monde nanoscopique sont très différentes de celles, classiques, qui gouvernent le monde macroscopique. En particulier, elles impliquent une logique non classique où une porte peut être simultanément ouverte et fermée. Elles fascinent les esprits curieux tout en leur semblant hors de portée alors qu'il n'en est rien : l'optique physique, enseignée traditionnellement comme l'étude des lois de la réflexion, de la réfraction, de la polarisation, de la diffraction et de l'interférence de la lumière est quantique par essence et son étude constitue l'approche la plus immédiate de ce monde étonnant. Celui qui étudie l'optique est comme Monsieur Jourdain, il fait de la physique quantique sans (peut-être) le savoir.
Le statut d'une théorie physique.
La physique ambitionne de compresser l'ensemble des observations faites à propos des systèmes qu'elle étudie. Elle y parvient au moyen d'un modèle mathématique - ou plus généralement informatique - aussi concis que possible. On distingue trois phases :
- Le temps de l’observation, celui où l’on collecte un maximum de données relatives aux phénomènes qui se produisent spontanément dans la nature ou à ceux que révèlent l’expérimentation en laboratoire.
- Le temps de la modélisation mathématique, celui où l'on tente de compresser l’ensemble les données collectées en un programme (au sens informatique du terme) aussi court que possible. Ce programme doit être capable de recalculer, sans perte, les données compressées et de les imprimer au terme d'une exécution qui se termine.
- Le temps de l’interprétation, celui qui décrit le programme compresseur dans le langage de tous les jours afin d’en permettre la diffusion et l'enseignement dans le cadre d'une logique acceptée par le plus grand nombre.
Cette démarche ne se déroule pas toujours aussi idéalement et les exemples abondent de théories qui, ayant trouvé leurs limites, doivent être repensées voire bouleversées. L'optique physique offre un bel exemple d'une théorie qui a évolué au cours des siècles, à mesure que les données expérimentales se sont affinées.
L'optique physique des origines à nos jours.
Dès la seconde moitié du 17ème siècle, l'optique naissante a proposé deux modèles théoriques rivaux :
- Le modèle géométrique (Newton, Snellius, Descartes, Fermat), considère que la lumière se propage selon des trajectoires (rayons) généralement rectilignes mais brisées au contact d'un obstacle réfléchissant (miroir) ou réfractant (dioptre). On imagine que ces auteurs avaient en tête que les rayons lumineux étaient parcourus par des corpuscules de lumière, sans autre précision puisque le photon était inconnu à cette époque.
- Le modèle ondulatoire (Huygens, Fresnel, Young, Malus), assimile la lumière à une onde centrée sur un point source, éventuellement une infinité si la source est large. Cette onde est censée se propager de proche en proche : à tout instant, t, les points atteints par l'onde et constituant son front deviennent autant de sources secondaires d'ondelettes qui interfèrent entre elles, par superposition algébrique, pour construire le nouveau front d'onde, à l'instant, t+Δt.
Bien que ces deux approches soient encore enseignées de nos jours, la première dans le cycle élémentaire et la seconde dans le cycle supérieur, il est établi, depuis les travaux de Thomas Young, vers 1800, que l'approche géométrique est inadaptée car elle n'explique correctement que la réflexion et la réfraction, échouant à expliquer la diffraction, l'interférence et la polarisation.
L'approche ondulatoire est certainement très supérieure puisqu'elle explique tous les phénomènes précités. Vers 1865, James Maxwell a précisé la nature électromagnétique de cette onde, composée de deux champs couplés, l'un électrique et l'autre (d'induction) magnétique, tous deux transversaux par rapport à la direction de propagation. Il également trouvé les équations de propagation auxquels ces champs obéissent (Equations de Maxwell).
L'expérience de Taylor.
L'histoire semblait terminée et pourtant elle ne l'était pas, le modèle ondulatoire finissant lui aussi par trouver ses limites :
- Dès 1839, Antoine Becquerel, le grand-père du futur prix Nobel, Henri Becquerel, a mis en évidence un embryon d'effet photoélectrique qui aurait dû mettre la puce à l'oreille des physiciens. Personne à l'époque n'a véritablement compris l'importance de cette découverte qui, de fait, ne sera complètement élucidée qu'en 1905, par Albert Einstein, sur base d'un modèle qui semble faire machine arrière puisqu'il remplace l'onde par le photon.
- En 1909, le physicien anglais, Geoffrey Ingram Taylor a publié les résultats d'une expérience décisive qui a sonné le glas de la théorie ondulatoire et (définitivement ?) accrédité celle du photon.

Taylor a eu l'idée d'exposer une plaque photographique au rayonnement d'une source lumineuse atténuée à l'extrême. Le résultat a surpris tout le monde : la plaque s'est trouvée progressivement impressionnée en des points isolés, répartis aléatoirement. Une conclusion s'imposait : la lumière est faite de corpuscules, les photons, confirmant une intuition que Newton avait eue en son temps, sans avoir jamais eu les moyens de l'étayer, et qu'Einstein venait de réactiver.
Taylor a ensuite réitéré l'expérience d'interférence d'Young dans ces conditions extrêmes, en interposant entre la source et le détecteur (= la plaque photographique) un écran opaque percé de deux fentes parallèles, minces et rapprochées. Les impacts lumineux sont restés aléatoires sous la seule contrainte de construire petit à petit le schéma des franges caractéristiques du phénomène d'interférence. Les figures (a, b, c, d et e) correspondent à des temps de pose croissants que Taylor a poussés jusqu'à plusieurs mois !
Ce phénomène d'interférence par les fentes était connu à l'époque de Young mais les intensités lumineuses qu'il manipulait étaient telles que, chaque seconde, pas moins de 1020 photons tombaient sur l'écran, ce qui occultait complètement le caractère discret des impacts.
Les décennies qui ont suivi la découverte de Taylor ont été marquées par une confusion extrême tant les théories ondulatoire et corpusculaire semblaient inconciliables. Un dilemme s'est posé à ce stade : fallait-il abandonner la théorie ondulatoire, pourtant féconde, et tout recommencer à zéro ou tenter une conciliation (L'invraisemblable "Dualité onde-corpuscule", relevant davantage du tour de passe-passe que de la science) ? Richard Feynman a levé toute ambiguïté dans sa thèse doctorale (1942), jetant les bases d'une électrodynamique quantique où le photon est au coeur du phénomène lumineux. Il en existe plusieurs présentations équivalentes dont la plus élégante repose sur la théorie quantique de l'information, c'est celle que nous adoptons pour la suite. Feynman a également proposé un modèle simplifié, lors de quatre conférences destinées à un public large, adaptées ici en français.
Une expérience, due Mach et Zehnder, illustre parfaitement le problème qui se pose : de base, il s'agit d'une banale interférence que la théorie ondulatoire est capable d'expliquer ... sauf que, la lumière étant faite de photons, il faut trouver une autre explication ! Un modèle purement corpusculaire est en fait concevable mais il bouleverse la logique en usage, qui doit être quantique et non plus classique.
L'expérience de Mach-Zehnder.
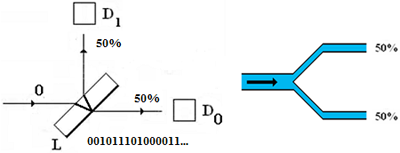
Lorsqu'une lame semi-transparente, orientée à 45 °, reçoit des photons émis au compte-gouttes, on observe qu'elle les distribue aléatoirement vers les détecteurs D0 et D1. Plus précisément, si l'on code par 0 (resp. par 1) l'enregistrement d'un photon par le détecteur, D0 (resp. D1), on trouve que la suite ordonnée des 0 et des 1 est aléatoire (au sens de Kolmogorov). Jusque-là rien d'intrigant : on pourrait imaginer un mécanisme complexe, caché à l'intérieur de la lame, qui serait responsable de ce tri, à la manière de ce qui se produit lorsqu'un canal distribue les molécules d'eau entre deux canaux plus petits.
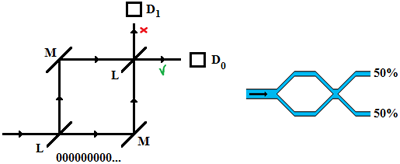
Les choses deviennent nettement étranges lorsqu'on complète le montage par l'adjonction, en série, d'une deuxième lame semi-transparente. Deux miroirs, inclinés à 45°, sont ajoutés afin que la rencontre ait lieu. Le résultat de l'expérience est sans appel : tous les photons sont détectés par D0, l'analogie hydraulique ne vaut manifestement rien ! Précisons que si les photons incidents sont initialement orientés dans la direction S-N (au lieu de O-E, comme sur la figure), alors c'est D1 qui enregistre l'arrivée de tous les photons. Cette expérience est troublante car les deux lames fonctionnent indépendamment et aucun raisonnement de logique classique ne peut expliquer que du hasard + du hasard puisse donner une certitude.
Lorsque les physiciens sont confrontés à un ensemble de phénomènes inexpliqués, la seule attitude raisonnable consiste à mettre au point, sans a priori, un modèle mathématique non contradictoire capable de rendre compte des observations. Ce modèle existe et il a été développé dans le cadre de la théorie quantique de l'information. Il repose sur une algèbre simple des états de base qui définissent le bit quantique (qubit). Cette algèbre et les règles qui l'accompagnent peuvent semblent tomber du ciel et, de fait, elles sont admises sans discussion par la communauté des physiciens précisément parce qu'elles décrivent correctement toutes les observations expérimentales recensées à ce jour. Chacun est libre de les refuser à condition de proposer autre chose qui fonctionne au moins aussi bien, ce qui ne s'est jamais produit !
La théorie quantique de l'information (Un exposé plus complet ici).
Tout système physique à deux états (au moins) peut encoder un bit d'information :
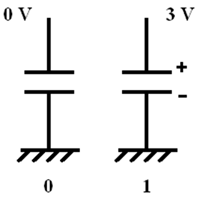
- Si ce système est classique, par exemple un transistor aux bornes duquel existe une tension électrique valant (par exemple) 0 V ou 3 V, ce bit vaut respectivement 0 ou 1, à l'exclusion de toute autre valeur. La logique (booléenne) sous-jacente est classique, posant qu'une proposition bien construite est obligatoirement vraie (V=1) ou fausse (F=0). Dans l'exemple du transistor, 100000 électrons (environ !) sont sans doute responsables de la tension observée et il importe peu qu'il en manque éventuellement 100 ou 1000 : ce bit est encodé de façon robuste. Il est également aisément manipulable, plus ou moins rapidement et au prix d'une dissipation calorifique bien connue des informaticiens.
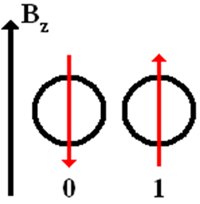
- Si ce système est quantique, par exemple un noyau atomique polarisé dans un champ magnétique extérieur, à la manière d'un aimant, on parle de qubit. Ce noyau isolé est fragile, la moindre perturbation extérieure pouvant le faire basculer d'une valeur 0 (ou 1) à l'autre. Vu sa petitesse, il est également délicat à manipuler (par imposition d'un champ magnétique extérieur convenablement piloté), par contre il ne connaît pas la dissipation car dans le monde atomique, les frottements (contre quoi ?) n'existent pas. Toutefois la différence essentielle est ailleurs : il cesse d'être vrai qu'un qubit ne peut prendre que les valeurs, 0 ou 1, à l'exclusion de toute autre : il peut également exister dans un état de superposition où il est simultanément 0 et 1. La logique sous-jacente cesse dès lors d'être classique, une proposition bien construite pouvant être simultanément vraie et fausse (certains préféreront dire, n'être ni vraie ni fausse).
Le photon autorise au moins deux modes d'encodage du qubit. Bien entendu l'algèbre définie s'applique dans les deux cas.
1) Etats spatiaux du photon.
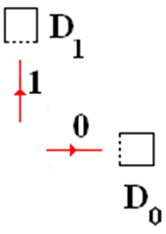
Tout photon issu d'une source peut être préparé dans l'un ou l'autre état spatial de base correspondant à un déplacement, sur une table d'optique, d'Ouest en Est (état |0>) ou de Sud en Nord (état |1>), à l'exclusion de tout autre (Les montages sont prévus pour que la table n'autorise pas les déplacements obliques).
Aussi longtemps qu'un photon, préparé initialement (en t=0) dans un état de base, ψ0 = |0> ou |1>, ne rencontre aucun obstacle, il demeure dans cet état, à un facteur de phase temporelle (inessentiel) près. Si l'on voulait être précis, il faudrait écrire l'état à l'instant t, ψt = exp[-2iπνt] ψ0, où ν est la fréquence du photon mais comme dans le vide tous les photons de même fréquence sont affectés du même facteur, on l'omet fréquemment même si on le sous-entend.
Par contre, lorsque ce photon rencontre un obstacle physique, la théorie quantique pose que son état bascule instantanément dans un nouvel état, conformément à la relation, ψaprès = U ψavant, où U est un opérateur (unitaire, cf infra) caractéristique de l'obstacle.
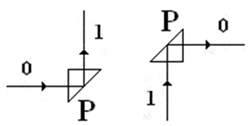
Par exemple, un prisme à réflexion totale (ou un miroir) inverse l'état spatial du photon, le faisant passer de |0> à |1> et inversement. L'opérateur qui garantit cette inversion se note, P = |0><1| + |1><0|, et cela demande quelques mots d'explications. En physique quantique, on distingue deux sortes de produits entre les vecteurs de base, |0> et |1>, et plus généralement entre n'importe quelles combinaisons linéaires (a |0> + b |1>) de ceux-ci :
- Les produits intérieurs (ou scalaires), du style <0||1>, sont des nombres, éventuellement complexes. Tout produit intérieur se calcule en appliquant la table de multiplication universelle entre vecteurs d'états :

En particulier, le produit intérieur d'un vecteur d'état par lui-même définit le carré de sa norme : |<0||0>|2 = |<1||1>|2 = 1. Tout vecteur d'état doit être normalisé à l'unité, pas seulement les vecteurs de base, on verra plus loin que c'est imposé par le fait que la probabilité totale de détection d'un photon doit valoir 1.
- Les produits extérieurs, du style |0><1|, constituent les opérateurs. Ils ne possèdent aucune signification en eux-mêmes, ils n'en acquièrent une que lorsqu'ils s'appliquent à un vecteur donné. Tel est le cas de l'opérateur identité, Id = |0><0| + |1><1|, qui laisse le photon intact ; on a bien : Id|0> = |0> et Id|1> = |1>. De même, dans le cas du miroir considéré plus haut, on vérifie que l'on a bien : P |0> = |0><1||0> + |1><0||0> = |1> et, de même, P |0> = |1>. En logique quantique, le miroir joue le rôle d'une porte NOT car il inverse les états V(rai) = 1 et F(aux) = 0.
Un opérateur physique, U, doit être unitaire, il doit satisfaire les relations, U*U = UU* = Id (où * note le conjugué complexe, s'il y a lieu). L'unitarité garantit la conservation de la norme du vecteur d'état lors de toute transformation du type, ψaprès = U ψavant, soit : |ψaprès|2 = |ψavant|2 = 1. Autrement dit, l'intégrité du photon en vol est préservée. Vérifions, par exemple, que la porte NOT est unitaire : PP = (|0><1| + |1><0|)(|0><1| + |1><0|) = |0><0| + |1><1| = Id.
Certains systèmes détruisent les photons en vol, c'est le cas des détecteurs qui fonctionnent par absorption. Les opérateurs qui représentent ces détecteurs ne sont donc pas unitaires, on les appelle des projecteurs. Notons D0 (resp. D1) les détecteurs de photons |0> (resp. |1>). Les projecteurs associés aux détecteurs, D0 et D1, se notent : D0 = |0><0| et D1 = |1><1|. Ils permettent de prédire la probabilité de détection d'un photon préparé dans un état donné, |état>, en suivant la règle : Proba(détection) = |D |état>|2. Voyons comment fonctionne cette règle dans deux cas particulièrement simples :
- On vérifie que si un photon se trouve dans l'un ou l'autre de ses états de base, |0> ou |1>, la probabilité de détection par D0 (resp. D1 ) vaut 1 ou 0 (resp. 0 ou 1), comme il se doit :
p0 = ||0><0||0>|2 = ||0>|2 = 1 et p1 = ||1><1||0>|2 = |0|2 = 0
p0 = ||0><0||1>|2 = |0|2 = 0 et p1 = ||1><1||1>|2 = ||1>|2 = 1
- Le facteur de phase temporelle accompagnant l'évolution d'un photon isolé n'affecte en rien sa probabilité de détection par un détecteur quel qu'il soit (C'est d'ailleurs pour cela qu'on l'omet souvent) :
|Dψt|2 = |exp[-2iπνt] Dψ0|2.
Ces deux exemples sont trop simples, il faut à présent considérer le cas où le photon n'est plus dans un état de base, |0> ou |1>. Un photon peut, en effet, exister dans un état de superposition, ψ = a |0> + b |1>, où il est à la fois |0> et |1> (certains préfèrent dire qu'il n'est ni |0> ni |1>). Les coefficients, a et b, sont des nombres éventuellement complexes mais dans tous les cas, ils sont liés par la relation de normalisation, |a|2 + |b|2 = 1. On garantit automatiquement cette normalisation en adoptant la forme trigonométrique équivalente pour le qubit, ψ = cos(θ) |0> + eiφ sin(θ) |1>. Nous verrons bientôt comment préparer un état superposé mais sachez d'emblée que les détecteurs, D0 et D1, ne sont absolument pas capables de le détecter comme tel. Si une telle opération était possible cela signifierait qu'on pourrait cloner un état de superposition inconnu, or cela est interdit par les lois de la mécanique quantique. Toute tentative de mesurer l'état (superposé) d'un photon aboutit à sa projection définitive sur l'état de base correspondant au détecteur qui l'enregistre. La seule utilité de connaître l'état de superposition est de prédire avec quelles probabilités les détecteurs, D0 ou D1, enregistreront le photon, on trouve (p0 + p1 = 1) :
p0 = ||0><0| (cos(θ) |0> + eiφ sin(θ) |1>)|2 = cos2θ et p1 = ||1><1| (cos(θ) |0> + eiφ sin(θ) |1>)|2 = sin2θ
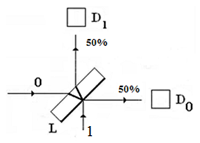
La lame semi-transparente symétrique, L, offre un bel exemple de création d'un état spatial superposé du type, ( |0> ± |1> )/✓2. Une telle lame transmet, par définition, une moitié de la lumière incidente et réfléchit l'autre moitié. L'opérateur associé à cette lame, encore appelé porte de Hadamard, se note, L = H = ( |0><0| + |0><1| + |1><0| - |1><1| )/✓2 (On trouvera quelques nuances dans l'exposé complet, car une réflexion sur une face plus réfringente provoque un déphasage de π, qu'on ignore dans une première approche afin de ne pas alourdir l'exposé; il y correspond un changement de signe sans importance). On vérifie deux choses :
- Cette lame transforme un photon incident, |0>, en un photon, H|0> = (|0> + |1>)/✓2 et un photon, |1>, en H|1> = (|0> - |1>)/✓2.
- Les probabilités de détection, à la sortie de cette lame, valent dans les deux cas, respectivement :
p0 = | |0><0| ( |0> ± |1> )/✓2|2 = 0.5 et p1 = | |1><1| ( |0> ± |1> )/✓2|2 = 0.5.
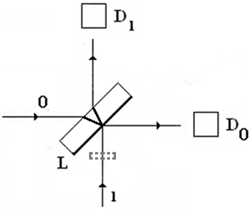
On modifie les états de sortie précédents, ( |0> ± |1> )/✓2, si l'on insère une lame, dite retardatrice, en verre d'indice de réfraction, n, et d'épaisseur, e, sur un chemin d'accès. Cette lame a pour effet de ralentir la lumière lors de sa traversée donc de créer un déphasage relatif, φ = -2πν(Δt) = -2πν(n-1)e/c. L'opérateur correspondant à un tel déphasage se note Φ0(φ) = eiφ |0><0| + |1><1| s'il affecte le canal associé à |0> et Φ1(φ) = |0><0| + eiφ |1><1| s'il affecte le canal associé à |1>. La porte de Hadamard représentée sur la figure ci-contre agit sur un canal |1> déphasé de φ, d'où elle se note : H' = Φ1(φ) H = |0><0| + |0><1| + eiφ |1><0| - eiφ |1><1|.
Note. Si la lame insérée est demi-onde (φ = π donc ei φ = -1), on voit que cela inverse deux signes sans que cela ait vraiment de l'importance pour la suite, c'est le sens de la remarque précédente. Beaucoup d'auteurs confondent sans dommage H et H'.
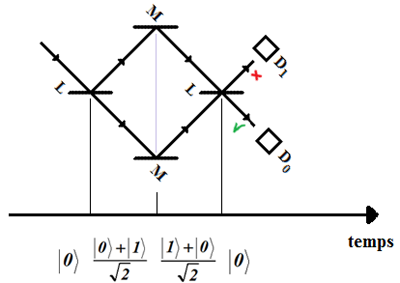
Nous sommes à présent en mesure de modéliser l'expérience de Mach-Zehnder. Commençons par faire subir une rotation de 45° au dessin du montage, afin de déployer horizontalement l'axe du temps et de suivre l'évolution du vecteur d'état, préparé initialement dans l'état, |0>.
Il subit, en séquence, les opérateurs correspondant aux obstacles qu'il rencontre dans l'ordre où ils se présentent, une lame semi-transparente, L, un miroir, M, et enfin une deuxième lame, L. Globalement, l'opérateur correspondant à l'interféromètre complet est le produit des opérateurs individuels : M-Z = LML. Le calcul de ce produit est facile mais un brin fastidieux, il livre le résultat suivant :
M-Z = (1/2) ( |0><0| + |0><1| + |1><0| - |1><1| ) ( |0><1| + |1><0| ) ( |0><0| + |0><1| + |1><0| - |1><1| ) = |0><0| + |1><1|
M-Z équivaut donc à l'identité : le modèle quantique prédit donc qu'un photon préparé dans l'état |0> (resp. |1>) retrouve cet état après avoir traversé l'interféromètre d'où il est toujours détecté par le détecteur correspondant, D0 (resp. D1), c'est bien ce qu'on observe.
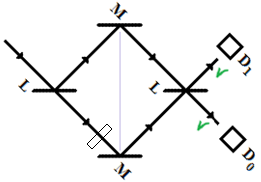
Si l'on modifie le montage de Mach-Zehnder en introduisant une lame retardatrice sur le bras intérieur correspondant à l'état |0>, cela oblige à introduire l'opérateur de déphasage, Φ0(φ) = eiφ |0><0| + |1><1|, dans le calcul de l'opérateur global :
M-Zmodifié = L Φ0(φ)ML = (1/2) ((eiφ+1) |0><0| + (-eiφ+1) |0><1| +(eiφ-1) |1><0| - (eiφ+1) |1><1|)
Appliqué à un photon préparé dans l'état |0>, cela donne :
M-Zmodifié |0> = 1/2 (eiφ+1) |0> + 1/2 (eiφ-1) |1>
Les détecteurs enregistreront le photon sortant aléatoirement mais avec des probabilités complémentaires fournies par la règle connue :
p0 = |1/2 (eiφ+1)|2 = cos2 (φ/2) et p1 = |1/2 (eiφ-1)|2 = sin2 (φ/2).
On voit que l'introduction d'une lame plus ou moins retardatrice fait varier les probabilités de détection mais que la probabilité totale vaut toujours 1, comme il se doit.
2) Etats de polarisation du photon.
L'expérience de Mach-Zehnder peut être recommencée sur base des états de polarisation du photon. Une théorie de la polarisation de la lumière existe depuis les travaux d'Etienne Louis Malus (1809) mais elle ne vaut que dans un cadre ondulatoire. Il est clair qu'elle doit être revue pour s'accorder au point de vue corpusculaire. On commence par rappeler la structure du photon telle que la physique quantique la décrit.
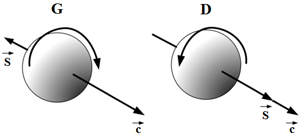
Voici les propriétés du photon :
- Dans le vide, il se propage en ligne droite, à la vitesse invariable, c = 299 792.458 km/s. Dans la matière cette vitesse est réduite d'un facteur, n, appelé indice de réfraction du milieu.
- Il possède une fréquence, ν, qui détermine sa "couleur" (visible ou non), une énergie, E = hν, et une quantité de mouvement, p = hν/c.
- Plus subtilement, comme une toupie en rotation, il possède un moment cinétique propre (= spin), aligné parallèlement (Sz = +1) ou antiparallèlement (Sz = -1) à sa direction de déplacement z. On pourrait dire que le photon est "vissé" à droite ou à gauche mais on préfère parler de polarisation (certains disent d'hélicité), droite (D) ou gauche (G). Dans un cadre classique, tout photon devrait être exclusivement gauche (état |G>) ou droit (état |D>). Toutefois le photon est un être quantique, il peut parfaitement se trouver dans un état de superposition, a |G> + b |D> (où les nombres, a et b, peuvent être complexes du moment qu'ils satisfont la relation de normalisation, |a|2 + |b|2 = 1 ). Deux exemples se rencontrent fréquemment :
- Les états, |x> = ( |D> + |G> )/✓2 et |y> = ( |D> - |G> )/(i ✓2), correspondent à deux états de polarisation linéaire selon deux axes transversaux orthogonaux, x et y. On les note indifféremment, |0> (ou p ou ∥) et |1> (ou s ou ⊥). Les relations inverses, |D> = ( |x> + i|y> )/✓2 et |G> = ( |x> - i|y> )/✓2, formalisent le passage de la polarisation linéaire vers la polarisation circulaire.
- Poursuivant, les états, |u> = ( |x> + |y> )/✓2 et |v> = ( |x> - |y> )/ ✓2, correspondent à deux états de polarisation linéaire selon deux axes transversaux inclinés à 45° par rapport aux orientations, x et y. Ces relations s'inversent sous les formes, |x> = ( |u> + |v> )/✓2 et |y> = ( |u> - |v> )/✓2.
Il est facile de préparer un photon dans l'état de base linéaire, |x> ou |y>, un polariseur linéaire suffit. Préparer un photon dans un état de polarisation circulaire est plus compliqué : on y parvient, par exemple, en deux temps, en le préparant dans un état de base linéaire, |x>, puis en l'obligeant à traverser une lame biréfringente correctement calibrée (Pour en savoir davantage sur les matériaux biréfringents, les modes de préparation des états de polarisation circulaires et la conception de portes de Hadamard, consultez éventuellement : Polarisation du photon et biréfringence).
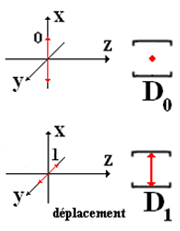
l'exposé de la théorie suivante n'est simple que si on raisonne à partir d'états de base polarisés linéairement selon les axes, x et y (|0> = |x> et |1> = |y>). On détecte (par absorption) les photons, |x> ou |y>, en plaçant sur leur trajectoire un (deuxième) polariseur (analyseur) dont la direction passante est orthogonale donc, orientée selon y ou x, respectivement. Les projecteurs associés à ces détecteurs demeurent inchangés, D0 = |0><0| et D1 = |1><1|.
Pour reproduire le montage de Mach-Zehnder en polarisation, on a besoin de (deux) portes de Hadamard. On les obtient (en polarisation linéaire) en taillant une lame biréfringente (d'épaisseur) demi-onde de telle façon que son axe optique soit perpendiculaire à la direction incidente, z, et faisant un angle, β = 22.5°, avec l'axe x. L'opérateur associé se note : Lame(22.5°,π) = i ( |0><0| + |0><1| + |1><0| - |1><1| ) = i H. Le facteur i (= eiπ/2) correspondant à un déphasage inessentiel de 90°.
Lorsqu'on envoie des photons, x = |0> (resp. y = |1>), sur une telle lame, ils en ressortent polarisés linéairement à + 45°) (resp. - 45°). Toute mesure effectuée à l'aide des détecteurs (x, y) enregistrera l'arrivée aléatoire d'un photon polarisé selon x et y, dans la proportion 50%-50%.
Le montage de Mach-Zehnder en polarisation comprend donc une source de photons, |0> = |x> (ou |1> = |y>), deux portes de Hadamard et deux détecteurs D0 = |0><0| et D1 = |1><1| (Les portes Not du montage spatial sont superflues car l'expérience se déroule le long d'un axe optique unique, z).
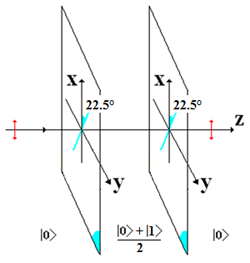
La deuxième lame biréfringente à 22.5° restaure tous les photons dans l'état initial, |x> (resp. |y>), bien qu'elle fonctionne de façon indépendante de la première ! Ce résultat est homologue à celui établi pour les états spatiaux, il n'est ni plus ni moins étonnant.
Si on intercale une lame de déphasage relatif, φ, entre les lames biréfringentes, les photons émergent du système complet, polarisés selon x ou y avec des probabilités (complémentaires) que l'on calcule à nouveau :
p0 = | |0><0| ( |0><0| + |0><1| + |1><0| - |1><1| ) ( exp[iφ] |0><0| + |1><1| ) ( |0><0| + |0><1| + |1><0| - |1><1| ) |0> |2 /4 = cos2(φ/2)
p1 = | |1><1| ( |0><0| + |0><1| + |1><0| - |1><1| ) ( exp[iφ] |0><0| + |1><1| ) ( |0><0| + |0><1| + |1><0| - |1><1| ) |0> |2 /4 = sin2(φ/2)
L'expérience de Mach-Zehnder montre le comportement quantique du photon mais elle n'est réalisable que dans un laboratoire bien équipé. Les deux expériences suivantes sont plus accessibles :
- L'effet tunnel.
Deux prismes droits, taillés à 45°, sont positionnés hypoténuse contre hypoténuse. La lame d'air qui les sépare est mince mais d'épaisseur non nulle, suffisante pour qu'une lumière incidente émise parallèlement aux bases subisse la réflexion totale, sans atteindre le second prisme. Cependant, si on rapproche les hypoténuses, on observe que l'intensité réfléchie diminue progressivement à mesure que la couche d'air emprisonnée s'amincit. Lorsque la pression exercée sur les faces atteint un certain seuil, plus aucune lumière n'est réfléchie. On réalise simplement une expérience similaire à l'aide d'un aquarium rempli d'eau : un doigt à peine posé sur une face est invisible pour l'oeil qui regarde sous l'angle de 45° au départ de la face adjacente mais il apparaît si on augmente la pression du doigt sauf au niveau du sillon des empreintes digitales qui emprisonnent une trop grande quantité d'air.
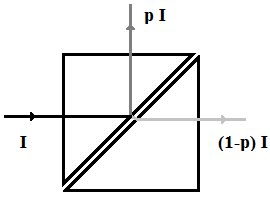
Effet tunnel - L'effet Zénon. Lorsqu'on éclaire, en lumière naturelle et avec une intensité I, deux polariseurs linéaires idéaux, croisés à 90°, disons selon x et y, il est bien connu qu'aucune lumière n'émerge du dispositif : le premier polariseur fonctionne comme un filtre préparateur d'un faisceau (d'intensité I/2) polarisé linéairement selon une direction unique, disons x, et le deuxième fonctionne comme un détecteur de photons |x>. Si l'on intercale un troisième polariseur linéaire idéal, à 45° des deux premiers, on observe qu'une moitié de l'intensité lumineuse de départ émerge à nouveau du système complet. Mieux encore, si l'on intercale, une suite de n polariseurs tournés à 90°/n (n=2, 3, 4, ...) du précédent, l'intensité émergente croît avec n pour rejoindre la valeur initiale, I/2, lorsque n tend vers l'infini. Les polariseurs intermédiaires agissent comme autant d'appareils de mesure à peine décalés les uns par rapports aux autres lorsque n est grand. Dans ces conditions, un très grand nombre de mesures successives ont pour effet de conduire une majorité de photons vers la sortie sans être détectés. Voyez-vous pourquoi cette expérience porte le nom du philosophe grec, Zénon d'Elée ?
Réflexion sur un miroir mobile
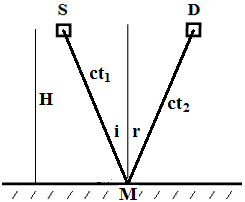
Le problème de la réflexion sur un miroir (plan) fixe est bien connu. Chacun a au moins appris à l'école élémentaire, que tout photon (ou rayon) lumineux émis au niveau d'une source ponctuelle, S, et détecté au niveau d'un détecteur ponctuel, D, a nécessairement transité, au niveau du miroir, par un point, M, situé à l'aplomb du milieu du segment SD. Autrement dit l'angle d'incidence, i, égale celui de réflexion, r, c'est la loi de la réflexion. Vous trouverez par ailleurs sur ce site une explication plus savante de cette loi, reposant sur le principe variationnel de Fermat : la trajectoire lumineuse allant de la source vers le détecteur via le miroir est celle qui rend le temps de vol extrémal, en l'occurrence minimal dans ce cas.
Il est intéressant de se demander ce que devient cette loi si le miroir est mobile (NDLR : cette chronique s'inspire librement d'un article publié par Kevin Brown dans l'ouvrage, Physics in Space and Time). Pour ne pas compliquer les choses, nous considérerons uniquement le cas d'un miroir qui recule (= s'éloigne de la droite SD) en translation uniforme à la vitesse constante, v. On présume, sans faire le moindre calcul, que rien ne change substantiellement si la vitesse v est très faible devant la vitesse de la lumière (v<<<c) : tout se passe comme si le miroir était fixe. Cela reste-t-il vrai lorsque v se rapproche plus ou moins de c ? On entre clairement dans le domaine de compétence de la relativité restreinte, d'où on pressent que le choix du système de référence peut jouer un rôle plus ou moins simplificateur dans le déroulement des calculs. Nous allons typiquement en considérer deux, celui lié au miroir (le plus simple) et ensuite celui lié à la source (et au détecteur). Le mouvement relatif de ces deux repères s'effectuant à la vitesse v, orientée perpendiculairement au miroir, on s'attend à ce que le déplacement éventuel, x, du point de contact de la lumière avec le miroir soit le même dans les deux cas. Cependant nous allons voir que la difficulté des calculs diffère notablement.
Référentiel lié au miroir.
Dans le référentiel lié au miroir, celui-ci est immobile par définition, et ce sont la source et le détecteur qui reculent, tous deux à la vitesse constante, v (orientée vers le haut sur la figure suivante). Les figures qui suivent présentent les trois instants remarquables : lorsque la lumière est émise, lorsqu'elle frappe le miroir et enfin lorsqu'elle est détectée. On note 2d la distance séparant la source du détecteur, H la distance de la source au miroir au moment précis où la lumière quitte la source et x la distance mesurant l'écart du point d'impact sur le miroir par rapport à l'aplomb.
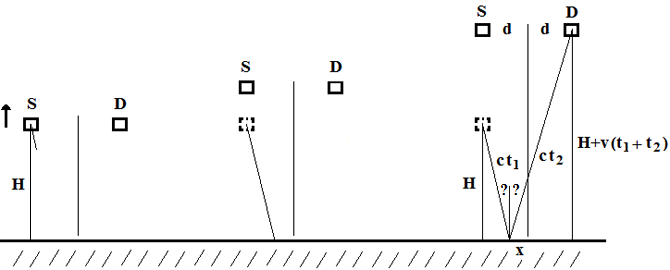
L'application du principe de Fermat exige de connaître préalablement le temps de vol complet, t1+t2. La figure de droite le permet par une double application du théorème de Pythagore, on trouve :
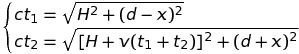
On détermine ensuite pour quelle valeur de x, (ct1 + ct2) est stationnaire. On a successivement :
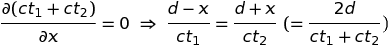
Ce résultat est particulièrement simple puisqu'il signifie que les angles d'incidence et de réflexion sont égaux comme si le miroir était fixe. Cela ne signifie cependant nullement que la distance x est nulle ! On le vérifie en éliminant t1 et t2 entre les trois équations précédentes, ce qui demande sinon de l'habileté du moins de la méthode (Les détails sont repris en annexe (Notebook Mathematica)). On trouve tous calculs faits :
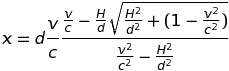
Les calculs qui précèdent sont élémentaires, requérant seulement de résoudre une équation du second degré. Il faut seulement prendre soin de retenir la seule racine garantissant que x s'annule avec v, ce qu'on vérifie aisément sur le résultat obtenu. A noter que la singularité apparente, lorsque v/c = H/d, n'en est pas réellement une; lorsqu'on lève l'indétermination, on trouve : x = (d2 + H2)/(2d). Les courbes suivantes affichent l'évolution de la distance, x, à mesure que le miroir s'écarte de la source pour 6 valeurs de la vitesse d'éloignement, choisies suffisamment proches de c pour qu'un effet de délocalisation par rapport à l'aplomb (x>0) soit décelable :
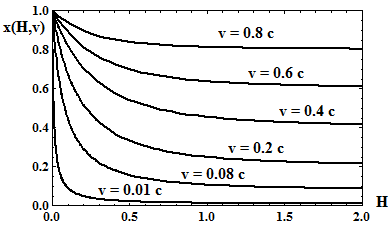
Sans surprise, pour toute valeur (non nulle) donnée de H, x tend vers zéro lorsque v tend vers zéro. Par contre, pour toute valeur donnée de v, x tend asymptotiquement vers d v/c (>0 !) à mesure que le miroir s'éloigne à l'infini.
Référentiel lié à la source et au détecteur.
On peut légitimement se demander en quoi il peut être utile de recommencer les calculs dans ce nouveau référentiel. Après tout, deux observateurs inertiels doivent pouvoir se mettre d'accord sur la même mesure d'un segment (x), orienté perpendiculairement à leur mouvement relatif, c'est imposé par la transformation relativiste de Lorentz. Pour vérifier que cela est bien vrai, il faut cependant prendre une précaution qui justifie l'intérêt qui est porté à ce calcul alternatif.
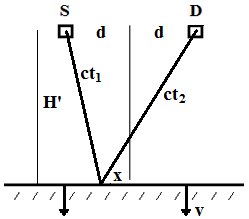
La figure est plus simple dans ce cas, il suffit de représenter le miroir en train de reculer, à la vitesse, v. Par contre, les calculs sont plus fastidieux car il se fait que les angles d'incidence et de réflexion ne sont plus égaux. Avant de lancer le calcul, observons que l'observateur lié au couple SD, mesure certainement les mêmes intervalles de temps, t1 et t2, que celui lié au miroir. Cela est dû au fait que la vitesse de la lumière vaut c dans tous les cas. Par contre, la distance, H', séparant la source du miroir au moment où la lumière est émise diffère à cause du phénomène de contraction de Lorentz. Il convient donc de poser, H' = H (1-v2/c2)1/2. A cette condition, les calculs effectués dans les deux référentiels doivent être d'accord sur la valeur de x.
L'application du principe de Fermat exige de connaître préalablement le temps de vol complet, t1+t2. On y parvient à nouveau par une double application du théorème de Pythagore, on trouve :
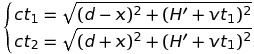
La première équation permet d'isoler la valeur de c t1, en fonction de x, puis la deuxième équation permet d'en faire autant pour c t2. Remplaçant H' par H (1-v2/c2)1/2, comme annoncé, il reste à exprimer le principe de Fermat en cherchant pour quelle valeur de x, le temps de vol total, t1 + t2, est stationnaire :
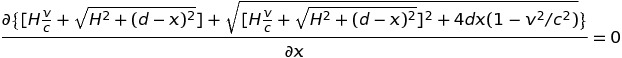
Les calculs détaillés demeurent élémentaires mais, réalisés à la main, ils sont encore plus fastidieux que dans le référentiel précédent. L'annexe jointe montre que le logiciel Mathematica s'en tire instantanément avec tous les honneurs. On retrouve la même formule pour le décalage, x, au niveau du miroir : comme promis, les deux observateurs sont donc d'accord sur le résultat final.
Note additionnelle. Lorsqu'une lumière émise par une source (ponctuelle) est recueillie au niveau d'un détecteur (ponctuel) en ayant transité par un obstacle (par exemple, un miroir), le principe de Fermat détermine la trajectoire lumineuse en rendant le temps de vol extrémal. Dans le cas du miroir plan, mais aussi d'un miroir convexe, cet extremum est un minimum mais cela cesse d'être le cas si le miroir est concave : dans ce cas c'est un maximum, l'exemple suivant le montre !
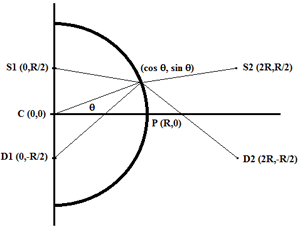
Ce miroir hémisphérique, de rayon unité (R = 1), est concave ou convexe selon que l'on situe la source en S1 ou en S2. Pour fixer les idées sur un exemple concret, les sources et les détecteurs ont été disposés symétriquement à un demi-rayon de distance de l'axe du miroir. Lorsque la lumière est détectée, respectivement en D1 ou en D2, tout le monde est d'accord pour reconnaître que la lumière a certainement transité par le point P, au niveau du miroir. Le principe de Fermat permet de retrouver ce résultat, il suffit de rendre extrémal les temps de vol totaux. On vérifie que l'extremum est un minimum dans le cas convexe mais un maximum dans le cas concave :
Miroir concave =
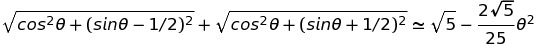
Miroir convexe :
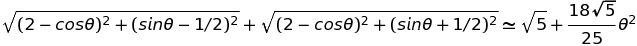
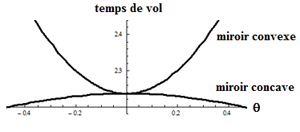
Expériences par la pensée en relativité restreinte
Préliminaires
Comme n'importe quelle théorie, la Relativité restreinte repose sur un ensemble de principes (axiomes, postulats, appelez-les comme vous voulez) présumés non contradictoires.
- Les plus anodins posent que la géométrie spatiale d'Euclide est d'application et que ses lois spatio-temporelles sont invariantes par translation (fixe) dans l'espace et dans le temps, par rotation (fixe) dans l'espace et par translation inertielle galiléenne. Ces principes ne valent que localement, dans une portion raisonnablement confinée de l'espace-temps (le domaine de validité de la Relativité restreinte), mais certains sont sans doute contestables (et de fait contestés) à l'échelle de l'univers où la Relativité générale prend effectivement le relais.
- Le plus surprenant pose que la vitesse de la lumière est finie et égale à c, une constante universelle, quel que soit l'état de mouvement (inertiel) de la source ou de l'observateur. On mesure d'emblée l'étrangeté de ce postulat qui semble contraire à l'intuition. Par exemple, si l'on poursuit la lumière en courant, on pourrait croire qu'on la réduit d'autant mais il n'en est rien et c'est l'un des triomphes d'Einstein d'avoir montré que ce principe tenait parfaitement la route.
- Un autre principe est d'une nature différente, disons opérationnelle. Il consiste à préciser (et à respecter !) un protocole expérimental capable de définir sans ambiguïté les coordonnées spatio-temporelles de n'importe quel événement. Pour fixer les coordonnées spatiales, la procédure est classique : on gradue préalablement les axes du référentiel à pas constant, d'où les coordonnées spatiales d'un événement sont celles du point où il se produit. Pour fixer la coordonnée temporelle, il convient d'être plus soigneux : il ne suffit pas de dire, comme le faisait Newton, que le temps s'écoule de façon invariable pour tout le monde donc qu'il est absolu. On pressent l'insuffisance de cette manière de faire en observant une étoile, peut-être une supernova qui explose, dont on reçoit la lumière avec un temps de retard, celui qu'il faut précisément à la lumière pour parvenir jusqu'à nous. L'incertitude qui plane sur l'attribution d'une coordonnée temporelle à cet événement est aggravée si deux observateurs en mouvement relatif sont concernés. L'idée fondamentale d'Einstein, à ce sujet, est que la coordonnée temporelle d'un événement est celle qui est indiquée par l'horloge située à l'endroit précis où il se produit. Il convient dès lors de déposer en tous points du référentiel des horloges fidèles et surtout de les synchroniser. Une manière d'y parvenir consiste à prérégler la position des aiguilles de chaque horloge sur l'heure, ℓ/c, variable selon la distance, ℓ, qui la sépare de l'origine des axes où l'on a déposé une source lumineuse isotrope. Lorsque cette source émet une lumière, celle-ci déclenche toutes les horloges sur son passage, ce qui a pour effet de les synchroniser sans ambiguïté vu la constance de c.
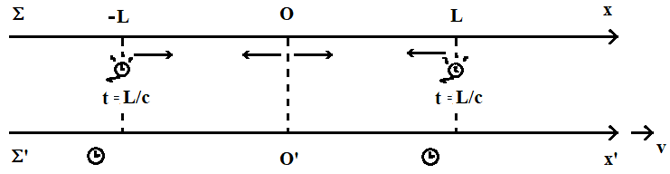
La figure ci-dessus illustre la mise en pratique de ces principe dans le cadre d'une expérience virtuelle préliminaire. Deux référentiels sont concernés, l'un, Σ, est "au repos" et l'autre, Σ', est en translation rectiligne uniforme (à la vitesse, v) par rapport à Σ. A l'instant t=t'=0, les axes (parallèles) sont alignés origine contre origine. Ils ne restent pas dans cet état puisque, pour t & t'>0, l'axe O'x' dérive vers la droite à la vitesse constante, v. L'expérience se déroule comme suit dans Σ : à l'instant, t=0, une source lumineuse située en O émet une lumière isotropiquement. Cette lumière a deux fonctions : 1) elle déclenche sur son passage les horloges préréglées sur l'heure, ℓ/c, en fonction de leur distance, ℓ, à l'origine (Phase de synchronisation des horloges) et 2) parvenue en x= ±L, elle fait exploser deux bombes (une de chaque côté) ou n'importe quels dispositifs capables de renvoyer instantanément de la lumière vers l'origine où elles finissent par se croiser. Trois événements successifs sont donc à considérer dans chaque référentiel :
- Dans Σ, tout est simple : 1) En t=0, deux photons sont émis symétriquement en O. 2) En t=L/c, ils activent simultanément les bombent situées en +L et -L, provoquant la réémission de deux nouveaux photons vers l'origine. 3) En t=2L/c, ces photons réémis se croisent simultanément en O. Au bilan, les bombes sont distantes de 2L et les phases 2 et 3 de l'expérience durent L/c chacune.
- Dans Σ', tout est moins simple : 1) En t'=0, deux photons sont émis symétriquement en O'=O, déclenchant la synchronisation des horloges de Σ', à ce stade rien ne change. 2) L'activation des bombes, telle que vue par O', ne se fait plus simultanément mais aux instants désignés par l(a position des aiguilles d)es horloges locales situées le long de O'x' en regard de ces bombes en train d'exploser. Or le fait que c n'est pas infini a pour conséquence que les horloges qui conviennent au repérage des explosions (= qui se trouveront en face de celles-ci au moment où elles se produisent) sont parties initialement d'une position légèrement en amont (<-L pour celle de gauche et <L pour celle de droite, comme indiqué sur la figure ci-avant). Vu la procédure de synchronisation, l'horloge de droite indique nécessairement un temps inférieur à celle de gauche, autrement dit, O' considère que la bombe de droite a explosé avant celle de gauche. Il y a donc perte de simultanéité. Par contre, le retour des photons réémis vers l'origine commune se fait nécessairement simultanément puisque c'est la même horloge qui témoigne du retour à la source.
Les lois de transformation de Lorentz
Le raisonnement précédent est délicat et, pour cette raison, la plupart des physiciens préfèrent s'en tenir aux formules de transformations (dites de Lorentz pour les coordonnées) reliant les coordonnées (x, t) et (x', t') et dont l'application est automatique et sûre. Elles diffèrent forcément des transformations classiques de Galilée (x' = x-vt & t'=t) qui ne garantissent pas la constance de c (x = ct ⇔ x' = ct' n'est pas vérifié). Elles s'écrivent :
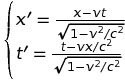
Note. Ces transformations impliquent effectivement la constance de c (Vérifiez !), par contre l'inverse n'est pas absolument vrai. Il est par exemple possible de proposer des transformations de type homographique qui possèdent aussi la propriété, x = ct ⇔ x' = ct'. Pour démontrer les relations de Lorentz, il ne suffit donc pas de s'en tenir à la constance de c, il faut encore prendre en compte l'invariance des lois par translation dans l'espace-temps, en particulier le principe d'inertie. Cela revient, au bilan, à n'accepter que des lois linéaires sur x & t. et x' & t'. Le lecteur qui souhaiterait approfondir ces questions peut consulter les ouvrages singuliers mais brillants de Kevin Brown, Reflections on Relativity et Physics in Space and Time, disponibles reliés chez l'éditeur online Lulu ou, gratuitement mais en pièces détachées, sur le site anonyme de l'auteur.
On peut contrôler les résultats de l'expérience préliminaire précédente sur base de ces transformations, où l'on pose, pour abréger, γ = (1-v2/c2)-1/2 : 1) Initialement on a : x=x'=0 et t=t'=0, cela se passe de commentaire. 2) Lorsque les bombes explosent, à droite (D) et à gauche (G), on a respectivement : xD = L & tD = L/c et xG = -L & tG = L/c. Les transformations de Lorentz traduisent immédiatement ces coordonnées dans le référentiel Σ' : x'D = γ (L-vL/c) & t'D = γ (L/c-vL/c2) et x'G = γ (-L-vL/c) & t'G = γ (L/c+vL/c2). On a bien la perte de simultanéité annoncée : t'D<t'G. 3) Lorsque les lumières réémises par les bombes reconvergent vers l'origine, on a : x=0 et t=2L/c, dans Σ, et x'=-γ 2L/c & t'=γ 2L/c, dans Σ'.
On en déduit que la durée totale de l'expérience vaut Δt = 2L/c, dans Σ, et Δt' = γ 2L/c = γ Δt (>Δt), dans Σ'; c'est la dilatation du temps perçue par l'observateur en mouvement par rapport aux bombes. A ce stade des calculs, il y a un piège qu'il convient d'éviter. On pourrait être tenté de poursuivre par le raisonnement suivant : la distance séparant les bombes valant incontestablement, xD-xG = Δx = 2L, dans Σ, on pourrait croire qu'elle vaut, x'D-x'G = Δx' = γ 2L = γ Δx, dans Σ' mais c'est faux ! L'erreur provient de ce que t'D ≠ t'G et qu'il est évidemment exclu qu'un observateur repère les extrémités d'une règle en mouvement (afin d'en déduire sa longueur) à des instants différents. Pour faire les choses correctement, il faut procéder autrement : on part des formules générales, x'D = γ (xD-vtD) & t'D = γ (tD-vxD/c2) et x'G = γ (xG-vtG) & t'G= γ (tG-vxG/c2), puis on impose que t'D = t'G, ce qui exige que xD-xG = (v/c2)(xD-xG), d'où finalement après quelques manipulations, Δx' = Δx/γ (<Δx), c'est la contraction des longueurs perçue par l'observateur en mouvement relatif (O' voit la distance entre les bombes plus petite que O, qui est au repos).
Il devrait être clair, dans le raisonnement précédent, que c'est la finitude de la vitesse de propagation de la lumière qui implique la contraction des longueurs longitudinales pour tout observateur en mouvement, du fait que celui-ci avance pendant que la lumière chemine d'un point à un autre. L'argument est sans effet si les distances considérées sont transversales (par rapport à v, ici selon les axes y ou z) et celles-ci sont de fait perçues de la même façon par O et O' : on peut donc compléter les transformations de Lorentz pour les coordonnées par les relations élémentaires, y=y' et z=z'.
Il existe également des transformations de Lorentz pour les champs, électrique et magnétique, qui assurent l'invariance des équations de Maxwell (On les a établies par ailleurs en se servant du formalisme quaternionique). Elles se notent comme suit, en vue d'une utilisation ultérieure :
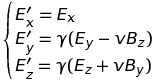
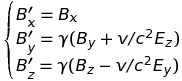
Le principe d'une expérience par la pensée
Une expérience par la pensée imagine un protocole expérimental, éventuellement fictif, et en prédit l'évolution dans le cadre de la théorie en cours. L'idée est de s'assurer qu'aucune contradiction interne n'apparaît qui condamnerait l'usage de cette théorie. Insistons sur le fait qu'il importe peu que les expériences décrites soient éventuellement difficiles voire impossibles à mettre en oeuvre expérimentalement, seule la cohérence logique de la théorie est en question.
Galilée a été le premier a utiliser ce mode de pensée dans le cadre des premiers pas de la mécanique classique mais c'est sans doute la (théorie de la) relativité restreinte qui en a fait le plus large usage.
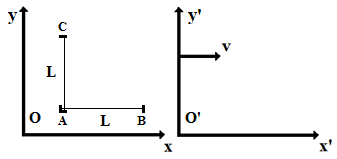
Un montage est commun à plusieurs expériences décrites ci-après : dans le référentiel fixe, Σ, dit "au repos" (d'axes Ox, Oy, Oz) et lié à l'observateur, O, des particules matérielles ou des photons voyagent à vitesse constante parallèlement à l'axe x (par exemple selon AB ou BA) ou parallèlement à l'axe y (selon AC ou CA). Les bornes A, B et C, fonctionnent éventuellement comme des miroirs fixes (donc infiniment lourds, afin d'éviter tout recul) : en cas de collision ils renvoient les particules ou les photons en inversant simplement leur vitesse. La scène est décrite simultanément dans le référentiel, Σ', dit "en mouvement" (d'axes O'x', O'y', O'z') et lié à l'observateur O'. Σ' est en translation rectiligne uniforme selon Ox (initialement confondu avec O'x', y compris les origines, O'=O), à la vitesse, v, par rapport à Σ. Pour chaque expérience, les observateurs, O et O', comparent leurs observations afin de vérifier leur cohérence.
Naturellement Σ est également en translation par rapport à Σ', à la vitesse opposée, -v, d'où il devrait être clair, une fois pour toutes, que les miroirs, immobiles dans le référentiel lié à O, se déplacent en bloc vers la gauche à la vitesse, -v, lorsqu'ils sont vus dans le référentiel lié à O'.
Exp. 1 : Dilatation du temps
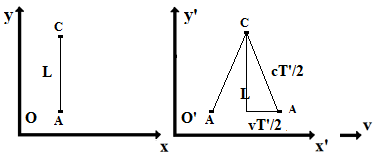
Dans cette expérience, deux miroirs, A et C, distants de L, sont orientés, dans Σ, parallèlement à Ox, le long d'une parallèle à Oy. Ils se renvoient continuellement une lumière émise initialement en A dans la direction de C. Pour O, tout est simple : les miroirs sont immobiles et le phénomène est un va-et-vient périodique. La période temporelle, T, correspondant à un aller-retour complet, vaut naturellement, T=2L/c. Pour O', le système des miroirs recule à la vitesse, -v : le phénomène demeure périodique, avec la période T', mais il est vu comme un déplacement lumineux en zigzag, à la vitesse, c, inchangée par principe. Pour les deux observateurs, ce système fonctionne comme le tic-tac d'une horloge sans qu'il y ait de raison de penser que les périodes T et T' sont égales. De fait, on démontre comme suit qu'elles diffèrent. Dans Σ', pendant un trajet aller-simple (une demi-période, T'/2), le miroir supérieur recule de vT'/2 et la lumière parcourt obliquement la distance, cT'/2. La figure ci-contre fait apparaître un triangle rectangle avec pour côtés, l'hypoténuse, cT'/2, et les côtés de l'angle droit, L et vT'/2. Le théorème de Pythagore relie ces côtés comme suit, (cT'/2)2 = (vT'/2)2 + L2 = (vT'/2)2 + (cT/2)2, soit : T' = T/(1-v2/c2)1/2, c'est la dilatation du temps telle que perçue par O'. On note que la différence d'ordonnées entre les miroirs a été posée égale à L dans les deux référentiels puisque les distances orthogonales au déplacement relatif de deux observateurs (inertiels) sont toujours perçues égales.
Exp. 2 : Contraction des longueurs (longitudinales)
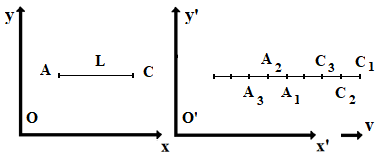
Modifions le montage précédent en faisant tourner le système des miroirs de 90° dans le sens horlogique; la lumière est encore émise de A vers C, mais à présent parallèlement à Ox. Pour O, les photons lumineux effectuent à nouveau un aller-retour périodique et la période demeure égale à, T=2L/c. Pour O', la situation se complique : il observe un va-et-vient régulier du photon émis, épousant le motif, A1, C1, A2, C2, A3, C3, .... Toutefois les trajets allers (de Ai vers Ci) et retours (de Ci vers Ai+1) prennent des temps différents, T'1 et T'2, du fait du recul permanent des miroirs. De plus, la distance, L', qui sépare les miroirs en train de reculer diffère de L. On calcule les temps comme suit : 1) Premier temps (aller) : T'1= (L' - v T'1)/c, d'où T'1 = L'/(c+v) et 2) Deuxième temps (retour) : T'2 = (L' + v T'2)/c, d'où T'2 = L'/(c-v). Au bilan, T' = T'1+T'2 = 2L'c/(c2-v2). Au terme d'un cycle complet, les deux observateurs sont d'accords que le photon a réintégré sa source, d'où les périodes qu'ils enregistrent doivent être dans le même rapport que lors de l'exp. n°1, soit, T' = T/(1-v2/c2)1/2. Vu la valeur trouvée pour T, T=2L/c, cela n'est possible que si la distance entre les miroirs, est perçue plus courte, par O', dans le rapport : L' = L (1-v2/c2)1/2. C'est la formule de contraction des longueurs longitudinales (= parallèles au mouvement relatif des observateurs).
Exp. 3 : Composition de vitesses orthogonales
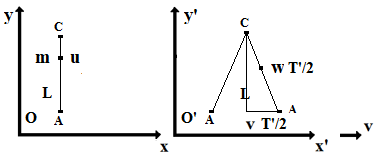
L'invariance postulée de la vitesse, c, est manifestement en contradiction avec la loi classique d'addition vectorielle des vitesses (w=u+v, si u et v sont parallèles, et w=(u2+v2)1/2, si elles sont perpendiculaires). Ces lois doivent donc être modifiées sans entraîner pour autant de grands bouleversements à l'échelle des vitesses usuelles où elles donnent satisfaction. Dans le cas où u et v sont perpendiculaires, on obtient la nouvelle loi en reconsidérant le montage de l'expérience n°1 sauf que le photon se déplaçant à vitesse, c, est remplacé par un corpuscule de masse, m, se déplaçant à vitesse, u<c, dans Σ. Ce corpuscule, émis disons en A, subit des rebonds parfaitement élastiques, alternativement en C puis en A, entraînant une cascade d'allers-retours périodiques de période, T = 2L/u. La même expérience vue dans Σ' fait état d'une trajectoire périodique en zigzag, à vitesse, w, avec une période dont nous savons depuis l'exp. 1 qu'elle doit valoir, T' = T/(1-v2/c2)1/2. Or le calcul direct de T' peut être calqué sur celui mené à l'exp. n°1; on trouve : (wT'/2)2 = L2 + (vT'/2)2. Remplaçant L par uT/2 et simplifiant par T, il reste, w2 = u2 + v2 - u2v2/c2, qui est la loi cherchée de composition des vitesses orthogonales. Cette loi respecte l'invariance de c (il suffit de poser u=c pour constater que w vaut à nouveau c) et elle se réduit à l'approximation classique, w2 = u2 + v2, aux faibles vitesses (le terme relativiste correctif est négligeable aux vitesses usuelles, nettement inférieures à c).
Exp. 4 : Composition de vitesses parallèles
Ce calcul pourtant calqué sur celui de l'expérience 2 est nettement plus délicat. Lorsque O' observe le va-et-vient de la particule se déplaçant selon O'x', il doit tenir compte du recul des miroirs. En fait ce n'est pas une mais deux lois de composition des vitesses qu'il doit découvrir même si elles sont évidemment corrélées par inversion de v. L'aller-retour complet se compose de deux tronçons prenant des temps différents, T'1 et T'2. On a successivement : T'1 = (L'-vT'1)/w1 d'où, T'1 = L'/(w1+v), et T'2 = (L'+vT'2)/w2 d'où, T'2 = L'/(w2-v). Au total, on a : T' = T'1+T'2 = L'(w1+w2)/[(w1+v)(w2-v)]. On doit encore avoir T' = T/(1-v2/c2)1/2, L' = L (1-v2/c2)1/2 et T = 2L/u, si bien qu'au bilan, les vitesses, w1 et w2, perçues par O', doivent satisfaire la relation, u(1-v2/c2)(w1+w2) = 2(w1+v)(w2-v). En principe, une relation ne suffit pas pour trouver deux inconnues (w1 et w2) mais celles-ci ne sont pas indépendantes puisqu'elles s'échangent par inversion des vitesses : w1= W(v) et w2= W(-v). L'équation fonctionnelle résultante, u(1-v2/c2)(W(v)+W(-v)) = 2(W(v)+v)(W(-v)-v), possède pourtant une infinité de solutions comme on le découvrirait, par exemple, en cherchant une solution sous la forme d'un développement en série de puissances de v autour de v=0.
Note. Ce résultat peut surprendre mais il est en accord avec la remarque formulée précédemment selon laquelle l'hypothèse de la constance de la vitesse de la lumière ne suffit pas pour déterminer (toutes) les lois de la relativité restreinte. Elle a certes suffi pour déterminer la loi de composition des vitesses orthogonales (Exp. n°3) mais elle échoue à démêler complètement le cas des vitesses parallèles. Il y a lieu pour s'en sortir d'invoquer à nouveau l'invariance par translation spatio-temporelle qui implique la linéarité des transformations de coordonnées donc, au niveau des vitesses, une loi homographique (rationnelle mais linéaire en ses termes).
La seule solution homographique qui satisfait l'équation fonctionnelle précédente s'écrit, W(v) = (u-v)/(1-uv/c2), qui correspond à la loi cherchée de composition des vitesses parallèles (et de même sens), w = (u-v)/(1-uv/c2). Si les vitesses u et v sont de sens contraire il suffit d'inverser le signe de v : w = (u+v)/(1+uv/c2).
Exp. 5 : Choc complètement inélastique
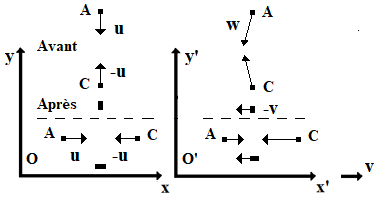
La discussion de la collision frontale (totalement) molle entre deux mobiles identiques permet de calculer, dans n'importe quel référentiel inertiel, l(a dépendance selon les vitesses d)es énergies cinétiques relativistes en jeu et la quantité de chaleur dégagée lors de la collision. Elle repose sur la conservation de l'énergie. On considère, dans Σ, deux particules identiques, animées des vitesses, +u et -u, entrant en collision frontale totalement inélastique. La figure ci-contre regroupe, l'un en-dessous de l'autre et en distinguant chaque fois les situations "avant" et "après" le choc, les cas parallèle à Oy et parallèle à Ox. Dans une collision totalement inélastique, le choc est complètement mou à la manière de deux mottes de beurre qui s'agglutineraient, n'en formant plus qu'une seule. Dans Σ, cette masse résultante s'immobilise instantanément tandis que dans Σ', elle chemine de droite à gauche avec la vitesse -v. Dans Σ, les énergies cinétiques initiales, K, sont donc intégralement dissipées en quantité de chaleur et déformation, Q, mais cela cesse d'être vrai dans Σ' car la masse agglutinée emporte une composante d'énergie cinétique du fait qu'elle recule. Les énergies cinétiques sont proportionnelles (~) aux masses au repos (mais celles-ci étant égales, elles n'ont pas besoin d'être précisées) et elles dépendent du module des vitesses ou, ce qui revient au même, de leur carré, K ~ f(u2). Dans Σ, peu importe que les particules entrent en collision parallèlement à Ox ou à Oy, le bilan énergétique est le même : 2f(u2) = Q. Cela cesse d'être vrai dans Σ', d'où la nécessité de distinguer les cas parrallèle et perpendiculaire à O'x'. Les lois déterminées aux points 3 et 4 sont utiles à ce stade. Si la collision a lieu selon Ox dans Σ, O' écrit, f[(u+v)/(1+uv/c2)] + f[(u-v)/(1-uv/c2)] = Q' + 2f(v2) tandis que si elle a eu lieu selon Oy, il écrit, 2f(u2+v2-u2 v2/c2) = Q' + 2f(v2). On note que rien ne dit que la quantité de chaleur dissipée est la même pour les deux observateurs, d'où les notations différentes, Q et Q', valables dans les référentiels correspondant, Σ et Σ' (Par contre, Q et Q' sont les mêmes, que la collision ait lieu selon Ox ou Oy). Les trois équations fonctionnelles qui précèdent peuvent être résolues exactement mais on se contente ici de donner la réponse que le lecteur peut à tout le moins vérifier s'il en a le courage : K ~ f(v2) = (1-v2/c2)-1/2-1 et Q' = Q/(1-v2/c2)1/2. La formule complète pour l'énergie cinétique, qui tient compte de la masse (au repos, m0) de la particule est, K = m0c2[(1-v2/c2)-1/2-1]. On vérifie aisément qu'on retrouve, aux faibles vitesses, la formule classique, K = m0v2/2. Cette formule peut être interprétée comme suit : l'énergie cinétique d'une particule est la différence de deux termes, mc2-m0c2, où m = m0(1-v2/c2)-1/2 est la masse en mouvement de la particule et m0 sa masse au repos; dans les deux cas, mc2 représente son contenu énergétique, qu'elle soit au repos ou en mouvement. C'est la loi célèbre, E = mc2.
Une discussion similaire, reposant sur la conservation de la quantité de mouvement, permettrait de (re)trouver la formule relativiste pour la quantité de mouvement d'un objet matériel, animé de la vitesse, v : p ~ v(1-v2/c2)-1/2. La formule complète, qui tient compte de la masse (au repos, m0) de la particule est, p = m0v(1-v2/c2)-1/2, qui restitue bien la formule classique, p = m0v, aux faibles vitesses. Les détails de cette discussion sont omis ici mais ils figurent dans les exposés soucieux de l'histoire de la relativité.
Exp. 6 : Absorption d'un photon par un atome
La discussion de l'émission ou de l'absorption d'un photon par un atome dans deux référentiels inertiels distincts repose sur la conservation de l'énergie et de la quantité de mouvement. Rappelons pour commencer 1) Que tout photon de fréquence, f, possède une énergie, E = hf, et une quantité de mouvement, p = hf/c (où h est la constante universelle de Planck) et 2) Que tout atome de masse au repos, m, et de vitesse, u, possède une énergie, E = mc2/(1-u2/c2)1/2 et une quantité de mouvement, p = m u/(1-u2/c2)1/2. Lorsque cet atome absorbe un photon, il passe dans un état excité de masse au repos, m*>m. L'émission est le phénomène inverse (L'atome se désexcite en émettant un photon) mais il n'est pas nécessaire de l'étudier car il ne nous apprendrait rien de neuf; on se limite donc ici au cas de l'absorption. Par contre, il y a lieu de distinguer le cas où la trajectoire du photon est transversale (perpendiculaire à v) et celui où elle est longitudinale (parallèle à v). Ils sont traités ci-après en séquence et dans chaque cas, la figure schématise le mécanisme tel que vu dans les deux référentiels (A gauche, Σ, et à droite, Σ'). Dans tous les cas, l'atome qui absorbe le photon recule en respectant les lois de conservation.
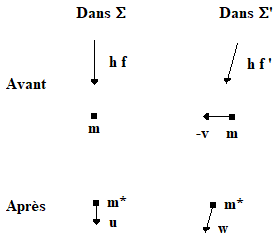
1er cas : Photon transversal. L'étude du cas transversal permet de comparer les fréquences photoniques mesurées par les observateurs O et O' (effet Doppler transversal). Dans ce cas simple, on n'a besoin que de la conservation de l'énergie dans les référentiels, Σ et Σ', soit respectivement : hf + mc2 = m*c2/(1-u2/c2)1/2 et hf' + mc2/(1-v2/c2)1/2 = m*c2/(1-w2/c2)1/2, où w est la vitesse de recul de l'atome calculée sur base de la loi de composition des vitesses orthogonales, u et v (w2 = u2 + v2 - u2v2/c2, pour rappel). Il "suffit" d'éliminer m* entre les deux équations précédentes pour trouver la relation qui relie obligatoirement f et f', à savoir, tous calculs faits : f' = f/(1-v2/c2)1/2, c'est la formule pour l'effet Doppler relativiste transversal. Note à l'usage du lecteur courageux qui voudrait tenter le calcul : celui-ci est grandement facilité par le fait que l'on a simplement, 1-w2/c2=(1-u2/c2)(1-v2/c2).
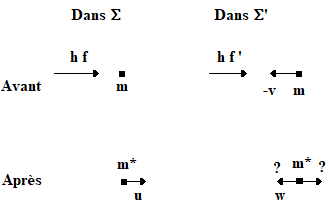
2ème cas : Photon longitudinal. L'étude du cas longitudinal permet à nouveau de comparer les fréquences photoniques mesurées par les observateurs O et O' (effet Doppler longitudinal). Ce cas est moins simple : outre la conservation de l'énergie dans les référentiels, Σ et Σ', soit respectivement, hf + mc2 = m*c2/(1-u2/c2)1/2 et hf' + mc2/(1-v2/c2)1/2 = m*c2/(1-w2/c2)1/2, où w est la vitesse de recul de l'atome calculée sur base de la loi de composition des vitesses parallèles, u et v (w = (u-v)/(1-uv/c2), pour rappel), on a aussi besoin de la conservation de la quantité de mouvement dans Σ, soit : h f/c = m*u/(1-u2/c2)1/2. Il "suffit" à présent d'éliminer m* et u entre ces trois équations pour trouver la relation qui relie obligatoirement f et f', à savoir, tous calculs faits : f' = f ((1-v/c)/(1+v/c))1/2, c'est la formule pour l'effet Doppler relativiste longitudinal. Note à l'usage du lecteur courageux qui voudrait tenter le calcul : celui-ci est grandement facilité par le fait que l'on a cette fois, 1-w2/c2=(1-u2/c2)(1-v2/c2)/(1-uv/c2)2.
Exp. 7 : Emission de deux photons identiques en opposition
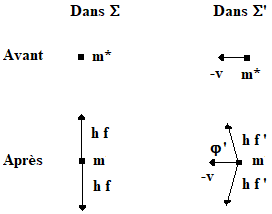
L'émission d'un seul photon (par un atome préalablement excité) ne donne rien de nouveau par rapport à l'absorption. Le cas où l'atome émettrait deux photons identiques en opposition dans Σ, à supposer que cela soit réaliste, est cependant intéressant, en ce qu'il permet de retrouver la loi relativiste pour le phénomène d'aberration transversale. La conservation de l'énergie se note dans les deux référentiels : m*c2 = 2h f + mc2 et m*c2/(1-v2/c2)1/2 = 2h f' + mc2/(1-v2/c2)1/2. Utilisées seules, ces relations ne font que retrouver l'effet Doppler transversal. Mais si on combine avec la conservation de la quantité de mouvement dans Σ', m*v/(1-v2/c2)1/2 = 2h f'/c cos(φ) + mv/(1-v2/c2)1/2, on trouve : cos(φ') = -v/c; c'est la formule pour l'aberration transversale qui indique comment la direction de propagation de la lumière est affectée du fait du mouvement (transversal) de l'observateur. Le même calcul effectué sur des photons émis longitudinalement permettrait de confirmer les lois Doppler longitudinales, f' = f ((1±v/c)/(1∓v/c))1/2 et de trouver une aberration longitudinale nulle.
Epilogue : lumière, onde ou photon ?
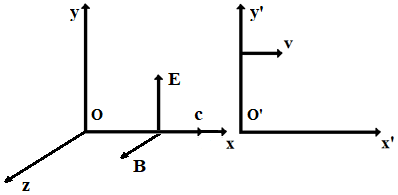
Les expériences précédentes couvrent une bonne partie des sujets abordés par Einstein dans son article fondateur sur la relativité (1905). On peut certainement simplifier la présentation en recourant aux lois de transformation de Lorentz mais ce serait au prix d'une perte de compréhension physique. Il est intéressant de rappeler qu'Einstein a simultanément préparé l'avènement de la mécanique quantique en introduisant la notion de photon lumineux. Avant cela, il était d'usage de penser que la lumière était exclusivement une onde électromagnétique, structurée sur la base de deux champs transversaux, l'un électrique (E) et l'autre magnétique (B, cf figure ci-contre). Dans ce cadre toujours enseigné, les deux champs sont parfaitement corrélés par les équations de Maxwell : dans le vide, ils évoluent en phase et leurs amplitudes sont proportionnelles, E0 = c B0. La densité d'énergie, 𝓌, portée par l'onde est proportionnelle au carré de son amplitude électrique selon la relation (ε0μ0 = 1/c2) : 𝓌 = 𝓌el + 𝓌magn = ε0E02/2 + μ0-1B02/2 = ε0E02. L'énergie emmagasinée dans un volume V vaut par conséquent, W = 𝓌 V.
Il est bien connu que la théorie ondulatoire de la lumière rend parfaitement compte des phénomènes optiques macroscopiques mais qu'elle échoue lorsqu'on descend dans l'échelle dimensionnelle (effet photoélectrique, par exemple). C'est d'ailleurs pour cette raison qu'Einstein a introduit la notion de photon lumineux. Un problème a cependant troublé les esprits, à l'époque, du fait que l'énergie du photon, E = h f, est proportionnelle à sa fréquence tandis que l'énergie de l'onde est proportionnelle au carré de son amplitude. Einstein ne disposait pas à cette époque des outils nécessaires pour réconcilier ces points de vue apparemment contradictoires (La mécanique quantique n'a été développée que 20 années plus tard). Tout au plus a-t-il noté une coïncidence heureuse dont il nous faut dire un mot : que l'on calcule l'énergie transportée par la lumière sur base de l'hypothèse ondulatoire ou corpusculaire, elle se transforme de la même manière lorsqu'on passe d'un observateur inertiel au repos à celui en mouvement uniforme. Autrement dit, la loi Doppler longitudinale, f' = f ((1-v/c)/(1+v/c))1/2, est exactement du même type que celle que prédit la théorie de Maxwell pour l'énergie transportée par l'onde électromagnétique. Voyons cela de plus près dans le cas d'une lumière polarisée linéairement selon Oy (= E parallèle à Oy). Le champ électrique vu par O évolue selon la loi sinusoïdale, E = Ey = E0 sin[2πf(t-x/c)] tandis que le champ magnétique associé suit la loi, B = Bz = (E0/c) sin[2πf(t-x/c)]. Pour connaître le champ électrique tel que vu par O', il suffit d'utiliser la relation de Lorentz rappelée en introduction, E'y = γ(Ey-vBz), ce qui donne, E'y = ((1-v/c)/(1+v/c))1/2E0 sin[2πf(t-x/c)], soit en repassant aux coordonnées, x' & t' (en inversant les transformations de Lorentz pour les coordonnées) : E'y = ((1-v/c)/(1+v/c))1/2E0 sin[2πf γ (1-v/c)(t'-x'/c)]. Vu que O' doit pouvoir écrire, E' = E'y = E'0 sin[2πf'(t'-x'/c)], on voit que la fréquence se transforme selon la loi Doppler, f' = f ((1-v/c)/(1+v/c))1/2, de même l'amplitude, E'0 = E0 ((1-v/c)/(1+v/c))1/2.
Les densités d'énergie, 𝓌, vues par O et O' étant proportionnelles aux carrés des amplitudes du champ électrique, on trouve : 𝓌'/𝓌 = (1-v/c)/(1+v/c). Pour obtenir les quantités d'énergie portée par l'onde, telles que vues par O et O', il faut encore multiplier ces densités par des volumes correspondants. On peut par exemple considérer, dans Σ, le volume limité par la surface sphérique progressant à vitesse c selon Ox, d'équation, (x-ct)2+y2+z2 = R2. Cette surface devient ellipsoïdale, dans Σ', et elle obéit à l'équation transformée, [(1-v/c)/(1+v/c)](x'-ct')2+y'2+z'2 = R2 (Passer aux coordonnées primées en inversant à nouveau les transformations de Lorentz). Les volumes correspondants valent, V = (4/3) π R3 et V' = (4/3) π R3 ((1+v/c)/(1-v/c))1/2, d'où V'/V = [(1+v/c)/(1-v/c)]1/2. Au bilan, E'/E = (𝓌'V'/𝓌V) = [(1-v/c)/(1+v/c)]1/2, soit exactement comme promis la même relation que pour le rapport, f'/f. Certes cela ne démontre pas la relation, E=hf, mais cela en renforce la plausibilité.
La physique du début du 20ème siècle a un temps vécu assise entre deux chaises, invoquant une hypothétique dualité onde-corpuscule. Ce dilemme a été tranché ultérieurement par Feynman dans ses exposés sur l'électrodynamique quantique (en faveur du point de vue corpusculaire, cf l'exposé élémentaire sur ce site). Les équations de Maxwell sont maintenant interprétées comme étant les équations d'onde du photon, avec le champ électrique incarnant sa fonction d'onde. Le carré de son amplitude donne la probabilité de présence des photons présents en très grand nombre dans l'onde macroscopique (chacun portant l'énergie, hf). Si l'on descend dans l'ordre dimensionnel, ce point de vue statistique perd toute signification et c'est le point de vue corpusculaire qui s'impose.